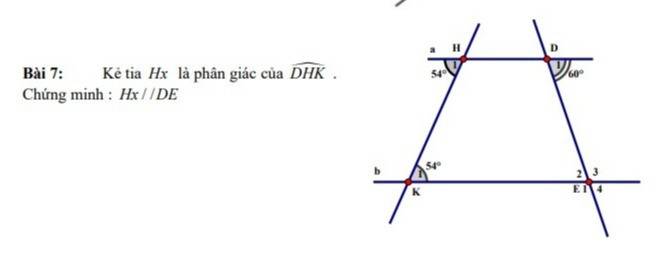
 help me bắt buộc phải vẽ hình vẽ giải thích ngắn nhất có thể pls
help me bắt buộc phải vẽ hình vẽ giải thích ngắn nhất có thể pls
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-acy}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-acy+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{y}{b}=\frac{z}{c}; \frac{z}{c}=\frac{x}{a}$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$

vì \(x\) và y là hai đại lượng tỉ lệ thuận nên \(x\) = ky
Thay \(x\) = 3; y = -9 vào biểu thức: \(x\) = ky ta có:
3 = k.(-9) ⇒ k = 3 : (-9) = - \(\dfrac{1}{3}\)
⇒ \(x\) = - \(\dfrac{1}{3}\)y
với \(x\) = -1,5 ta có: -1,5 = - \(\dfrac{1}{3}\)y ⇒ y = -1,5.(-3) = 4,5

Lời giải:
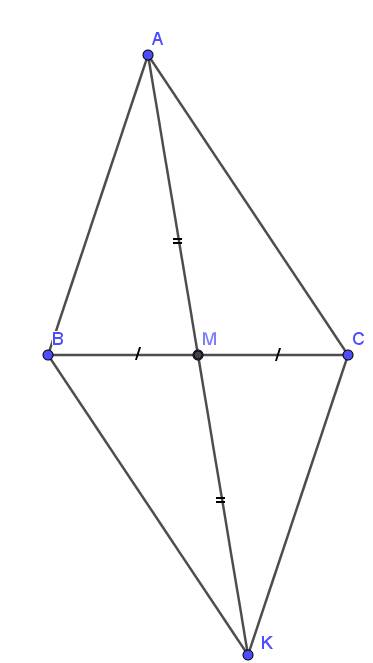
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$

2\(^x\) - 512 = 2y
2\(^x\) - 29 = 2y
2\(^9\).(2\(^{x-9}\) - 1) = 2y
2y = 29
⇒ y = 9
2\(x-9\) - 1 = 1
2\(^{x-9}\) = 1 + 1
2\(^{x-9}\) = 2
2\(^{x-9}\) = 21
\(x-9\) = 1
\(x\) = 1 + 9
\(x\) = 10
Nếu \(x\) = 9 ⇒ 2\(^9\).(20 - 1) = 0 ≠ 2y ∀ y \(\in\) N
Nếu \(x< 9\) ⇒ 2\(^x\) < 29 < 512 ⇒ 2\(^x\) - 512 < 512 - 512 = 0 (loại)
Nếu \(x\) > 10 thì 2\(^{x-9}\) là số chẵn
⇒2\(^{x-9}\) - 1 là số lẻ ⇒ 29.(2\(^{x-9}\) - 1) ≠ 29 ∀ \(x;y\in N\)
Vậy \(x=10;y=9\)
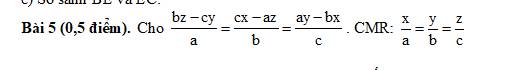
con cu
đề sai sai :'))