Lớp 6 chưa học giá trị tuyệt đối nhé bạn.

Bạn cứ trả lời đi

\(x\) = y.\(\dfrac{3}{4}\) ; z = \(\dfrac{y}{5}\).7

Thay \(x\) = y.\(\dfrac{3}{4}\) và z  = \(\dfrac{y}{5}\).7 vào biểu thức:

2\(x\) + 3y - z  = 186 ta có:

2.y.\(\dfrac{3}{4}\) + 3y - \(\dfrac{y}{5}\).7 = 186

y.(2.\(\dfrac{3}{4}\) + 3 - \(\dfrac{7}{5}\)) = 186

y.\(\dfrac{31}{10}\) = 186

 y = 186 : \(\dfrac{31}{10}\)

y = 60 ; \(x\) = 60. \(\dfrac{3}{4}\) = 45; z = 60.\(\dfrac{7}{5}\) = 84

\(x\) + y + z  = 45 + 60  + 84 = 189 

Mình không hiểu câu sau của đề bài.

Ta có: \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}\left(1\right)\)

\(\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\left(2\right)\)

Từ (1) và (2) suy ra:

\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{z}{28}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{z}{28}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{186}{62}=3\)

Do đó:

\(\dfrac{x}{15}=3\Rightarrow x=15.3=45\)

\(\dfrac{y}{20}=3\Rightarrow y=20.3=60\)

\(\dfrac{z}{28}=3\Rightarrow z=28.3=84\)

Tổng là: \(x+y+z=45+60+84=189\)

Vậy....

Lời giải:

$\frac{7x+5y}{3x-5y}=\frac{7z+5t}{3z-5t}$

$\Rightarrow (7x+5y)(3z-5t)=(7z+5t)(3x-5y)$

$\Rightarrow 21xz-35xt+15yz-25yt = 21xz-35yz+15xt-25yt$

$\Rightarrow -35xt+15yz=-35yz+15xt$

$\Rightarrow -50xt=-50yz$

$\Rightarrow xt=yz\Rightarrow \frac{x}{y}=\frac{z}{t}$

\(C=A-B=x^2-5xy+5y^2-3x+18y-\left(-x^2+3xy-y^2-x-7\right)\\ =x^2-5xy+5y^2-3x+18y+x^2-3xy+y^2+x+7\\ =\left(x^2+x^2\right)+\left(-5xy-3xy\right)+\left(5y^2+y^2\right)+\left(-3x+x\right)+18y+7\)

\(=2x^2-8xy+6y^2-2x+18y+7\)

Bạn xem lại đề nhé, mình nghĩ không tính được giá trị C khi x-y=4 nhé.

-3/4 . -8/9 . ... . -4084440/4084440

= 3/4 . 8/9 . 4084440/4084441

=1.3/2.2  .  2.4/3.3  ...  2020.2022/2021.2021

=1.3.2.4...2020.2022/2.2.3.3...2021.2021

=(1.2...2020)(3.4...2022)/(2.3...2021)(2.3...2021)

=1.2022/2021.2=2022/4042

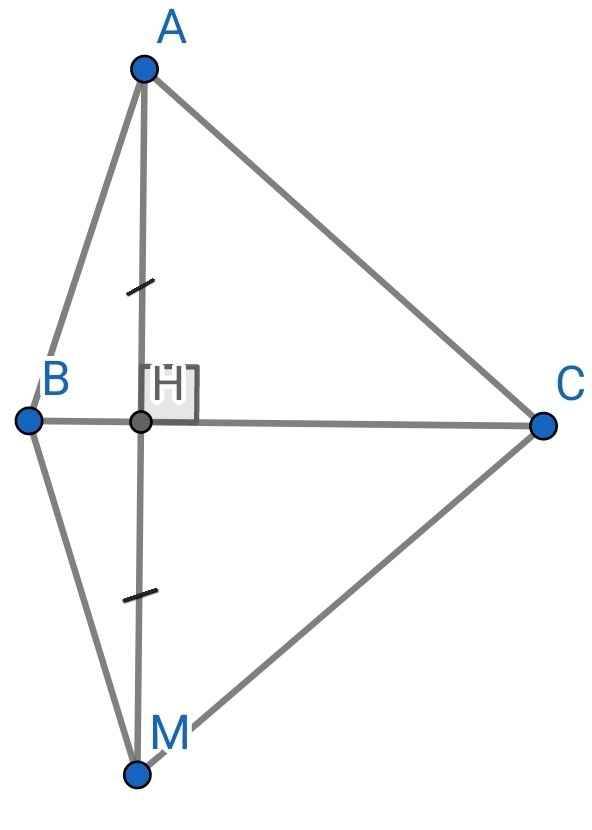 a) Xét hai tam giác vuông: ∆AHC và ∆MHC có:

HC là cạnh ccung

AH = MH (gt)

⇒ ∆AHC = ∆MHC (hai cạnh góc vuông)

b) Do ∆AHC = ∆MHC (cmt)

⇒ ∠ACH = ∠MCH (hai góc tương ứng)

AC = MC (hai cạnh tương ứng)

Do ∠ACH = ∠MCH (cmt)

⇒ ∠ACB = ∠MCB

Xét ∆ABC và ∆MBC có:

AC = MC (cmt)

∠ACB = ∠MCB (cmt)

BC là cạnh chung

⇒ ∆ABC = ∆MBC (c-g-c)

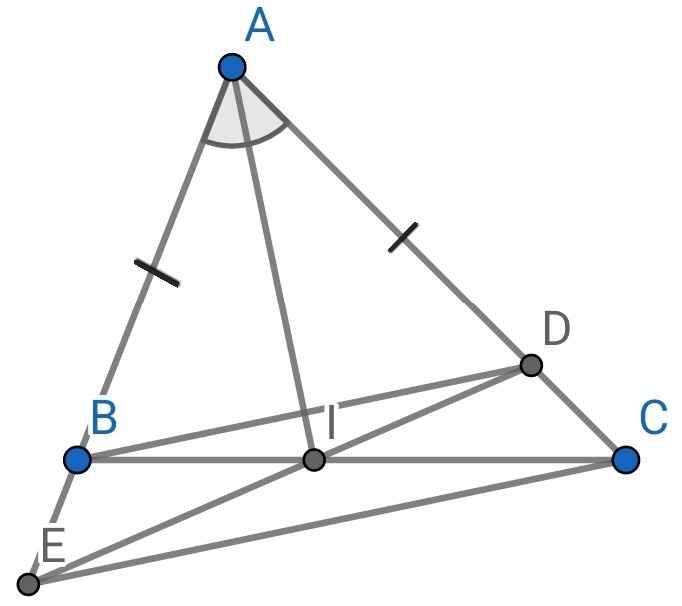
a) Do AI là tia phân giác của BAC (gt)

⇒ ∠BAI = ∠CAI

⇒ ∠BAI = ∠DAI

Xét ∆BAI và ∆DAI có:

AB = AD (gt)

∠BAI = ∠DAI (cmt)

AI là cạnh chung

⇒ ∆BAI = ∆DAI (c-g-c)

⇒ BI = ID (hai cạnh tương ứng)

b) Do ∆BAI = ∆DAI (cmt)

⇒ ∠ABI = ∠ADI (hai góc tương ứng)

Mà ∠ABI + ∠EBI = 180⁰ (kề bù)

∠ADI + ∠CDI = 180⁰ (kề bù)

⇒ ∠EBI = ∠CDI

Xét ∆IBE và ∆IDC có:

∠EBI = ∠CDI (cmt)

BI = ID (cmt)

∠BIE = ∠DIC (đối đỉnh)

⇒ ∆IBE = ∆IDC (g-c-g)

c) Do ∆IBE = ∆IDC (cmt)

⇒ BE = DC (hai cạnh tương ứng)

Mà AB = AD (gt)

⇒ AE = AB + BE = AD + DC = AC

∆AEC có:

AE = AC (cmt)

⇒ ∆AEC cân tại A

⇒ ∠AEC = (180⁰ - ∠EAC) : 2    (1)

∆ABD có:

AB = AD (gt)

⇒ ∆ABD cân tại A

⇒ ∠ABD = (180⁰ - ∠BAD) : 2 = (180⁰ - ∠EAC) : 2   (2)

Từ (1) và (2) ⇒ ∠AEC = ∠ABD

Mà ∠AEC và ∠ABD là hai góc đồng vị

⇒ BD // EC

a) \(\dfrac{1}{3}-\dfrac{1}{3}\times\left(2-\dfrac{3}{5}\right)\\ =\dfrac{1}{3}-\dfrac{1}{3}\times\dfrac{7}{5}\\ =\dfrac{1}{3}-\dfrac{7}{15}\\ =\dfrac{5}{15}-\dfrac{7}{15}\\ =-\dfrac{2}{15}\)

b) \(\dfrac{1}{9}-\dfrac{5}{15}+\dfrac{8}{9}-\dfrac{10}{15}+0,5\\ =\left(\dfrac{1}{9}+\dfrac{8}{9}\right)-\left(\dfrac{5}{15}+\dfrac{10}{15}\right)+0,5\\ =\dfrac{9}{9}-\dfrac{15}{15}+0,5\\ =1-1+0,5\\ =0,5\)

\(x^2+\dfrac{1}{4}=\dfrac{1}{2}\\ \Rightarrow x^2=\dfrac{1}{2}-\dfrac{1}{4}\\ \Rightarrow x^2=\dfrac{2}{4}-\dfrac{1}{4}\\ \Rightarrow x^2=\dfrac{1}{4}=\left(\pm\dfrac{1}{2}\right)^2\\ \Rightarrow x=\pm\dfrac{1}{2}\)