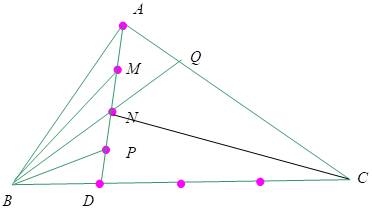
Cho tam giác vuông ABC ( A = 1v), đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E. Chứng minh: AE = BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Số người đủ cho mỗi thuyền 20 người nhiều hơn số người số người đủ cho mỗi thuyền 24 người là:
24+16=4024+16=40 (người)
24 người nhiều hơn 20 người là:
24−20=424−20=4 (người)
Số thuyền là:
40:4=1040:4=10 (thuyền)
Đơn vị có số người là:
24×9=21624×9=216 (người)
Đáp số:10 thuyền và 216 người.
Đây là toán hai hiệu số, chuyên đề thi chuyên thi học sinh giỏi các cấp, thi violympic. Hôm nay Olm sẽ hướng dẫn các me giải chi tiết dạng này như sau:
Giải:
Hiệu số người mỗi thuyền trong hai cách chở là:
20 - 15 = 5 (người)
Hiệu số người trong hai cách chở là:
40 + 20 = 60 (người)
Số thuyền là: 60 : 5 = 12 (thuyền)
Số bộ đội của đơn vị cần qua sông là:
12 x 15 + 40 = 220 (bộ đội)
Đáp số:...

tui biết làm mình câu a thui nha
a.Sbpd=1/4Sabd (vì...)
Sabd=1/4Sabc(vì...)
Sabd=5chia1/4=20(cm2)
Sabc=20chia1/4=80(cm2)

Lời giải:
$\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}=12$
$\Rightarrow \frac{a^2+b^2+c^2}{abc}=12$
$\Rightarrow a^2+b^2+c^2=12abc$
$\Rightarrow (a+b+c)^2-2(ab+bc+ac)=12abc$
$\Rightarrow -2(ab+bc+ac)=12abc$
$\Rightarrow \frac{ab+bc+ac}{abc}=\frac{12}{-2}$
$\Rightarrow M=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=-6$
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

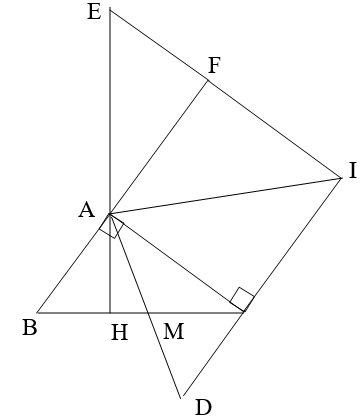
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\times AB\times AC=\dfrac{1}{2}\times6\times8=24\left(cm^2\right)\)
b: NB=4NC
=>\(BN=\dfrac{4}{5}BC\)
=>\(S_{ANB}=\dfrac{4}{5}\times S_{ABC}\)
MA=MB
=>M là trung điểm của AB
=>\(BM=\dfrac{1}{2}AB\)
=>\(S_{NMB}=\dfrac{1}{2}\times S_{NAB}=\dfrac{1}{2}\times\dfrac{4}{5}\times S_{ABC}=\dfrac{2}{5}\times S_{ABC}\)
=>\(S_{AMNC}=\dfrac{3}{5}\times S_{ABC}=24\times\dfrac{3}{5}=\dfrac{72}{5}\left(cm^2\right)\)

Chai nước rửa tay khô sau khi hết dịch bán 200000 đồng, đã ghi trong đề rồi mà bạn.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔABC~ΔHBA
=>\(\dfrac{AB}{HB}=\dfrac{BC}{BA}=\dfrac{AC}{HA}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)
c: Xét ΔAHB có AD là phân giác
nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)(1)
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{AH}{AB}\)(2)
Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{CAB}=90^0\)
\(\widehat{CDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HAD}\)(AD là phân giác của góc BAH)
nên \(\widehat{CAD}=\widehat{CDA}\)
=>CA=CD(3)
Từ (1),(2),(3) suy ra \(\dfrac{DH}{DB}=\dfrac{HC}{DC}\)
=>\(DH\cdot DC=HC\cdot DB\)

Giá tiền của chai nước rửa tay trong mùa dịch là:
200000x(1-10%)=180000(đồng)
Giá tiền của chai nước rửa tay sau mùa dịch là:
180000x(1+10%)=198000(đồng)

Vì \(x_1,x_2\) là 2 nghiệm của pt \(x^2-x-1=0\) nên:
\(x_1^2-x_1-1=x_2^2-x_2-1=0\)
Đồng thời, theo định lý Vi-ét, ta có:
\(x_1+x_2=1;x_1x_2=-1\)
Do đó \(B=\left(x_1^4-x_1^2\right)+x_2^2-x_1\)
\(B=x_1^2\left(x_1^2-1\right)+x_2^2-x_1\)
\(B=\left(x_1+1\right)x_1+x_2^2-x_1\)
\(B=x_1^2+x_2^2\)
\(B=\left(x_1+x_2\right)^2-2x_1x_2\)
\(B=1^2-2\left(-1\right)\)
\(B=3\)