`2/3 +5/3 x = 5/7`

`5/3x = 5/7 -2/3 = 15/21 - 14/21`

`5/3x =1/21`

`x =1/21 :5/3 = 1/21 *5/3`

`x = 1/35`

Vậy `x=1/35`

5/3x=5/7-2/3

5/3x=1/21

x=1/21.3/5

x=1/35

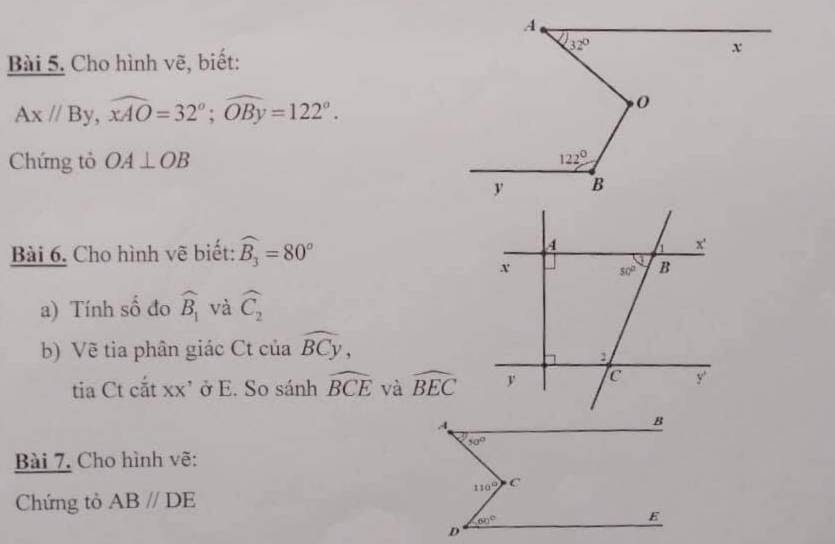
Đối với các bài hình học thì bạn chỉ nên đăng 1 bài/ 1 post thôi.

`3/4 : (2/3x - 1/2)=1/9`

`2/3x - 1/2 = 3/4 : 1/9`

`2/3x - 1/2 = 3/4 xx 9`

`2/3x - 1/2 = 27/4`

`2/3x = 27/4 + 1/2`

`2/3x = 27/4 + 2/4`

`2/3x = 29/4`

`x=29/4 : 2/3`

`x=29/4 xx 3/2`

`x = 87/8`

Giả sử \(\sqrt{2}\) là số hữu tỉ.

Khi đó tồn tại hai số nguyên a và b sao cho:

\(\sqrt{2}=\dfrac{a}{b}\)

\(\dfrac{a}{b}\) được viết dưới dạng phân số tối giản. 

Ta có:

\(\left(\sqrt{2}\right)^2=\left(\dfrac{a}{b}\right)^2\\ \Leftrightarrow2=\dfrac{a^2}{b^2}\\ \Leftrightarrow a^2=2b^2\)

Vì \(2b^2\) là số chẵn suy ra \(a^2\) chẵn, do đó a là số chẵn vì bình phương của một số là chẵn thì số đó chẵn.

Bởi vậy tồn tại số nguyên k sao cho a = 2k.

Suy ra: \(\left(2k\right)^2=2b^2\\ \Leftrightarrow4k^2=2b^2\\ \Rightarrow b^2=2k^2\)

Tương tự ta cũng suy ra được b là chẵn.

Bởi vậy \(\dfrac{a}{b}\) không phải phân số tối giản. Do đó không tồn tại a va b thõa mãn giả thiết. Suy ra \(\sqrt{2}\) là số vô tỉ

- \(\dfrac{3737}{4141}\) = - \(\dfrac{3737:101}{4141:101}\) = \(\dfrac{-37}{41}\)

vậy - \(\dfrac{3737}{4141}=-\dfrac{37}{41}\)

bằng nhau

giả sử \(\sqrt{2}\) là một số hữu tỉ như em nói ta có :

\(\sqrt{2}\) = \(\dfrac{a}{b}\) trong đó a,b ϵ N , b # 0 (a,b) =1

     \(\sqrt{2}\) = \(\dfrac{a}{b}\)

⇔  (\(\sqrt{2}\) )\(^2\) = (\(\dfrac{a}{b}\))² 

⇔ 2 =   \(\dfrac{a^2}{b^2}\)

⇔2.b² = a²

⇔ a² ⋮ 2 ⇔ a ⋮ 2 (1)

vì hai là số nguyên tố nên 

a² ⋮ 2 ⇔  a² ⋮ 4 ( t/c  của một số chính phương )

⇔ 2.b² ⋮ 4 ⇔ b² ⋮ 2 ⇔ b ⋮ 2 (2)

kết hợp (1) và(2) ta có:

\(\left\{{}\begin{matrix}a⋮2\\b⋮2\end{matrix}\right.\)

⇔ (a,b)  = 2 trái với giả sử (a,b) = 1

vậy điều giả sử là sai chứng tỏ \(\sqrt{2}\) không thể là số hữu tỉ nên \(\sqrt{2}\) là một số hữu tỉ

chúc rm thi tốt trong kì thi giữ kì 1 đang diễn ra em nhé 

cắt quả cam thành 20p