Vì AB//CD

nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}=\dfrac{1}{3}\)

=>\(OC=3OA;OD=3OB\)

Vì OC=3OA

nên \(S_{BOC}=3\times S_{AOB}=3\times6=18\left(cm^2\right)\)

Vì \(OD=3OB\)

nên \(S_{AOD}=3\times S_{AOB}=18\left(cm^2\right)\)

Vì OC=3OA

nên \(S_{DOC}=3\times S_{AOD}=54\left(cm^2\right)\)

\(S_{ABCD}=S_{ABO}+S_{BOC}+S_{DOC}+S_{AOD}\)

\(=6+18+18+54=96\left(cm^2\right)\)

Có phải diện tích hình thang ABCD là 78cm2 ko mọi người 

Lời giải:

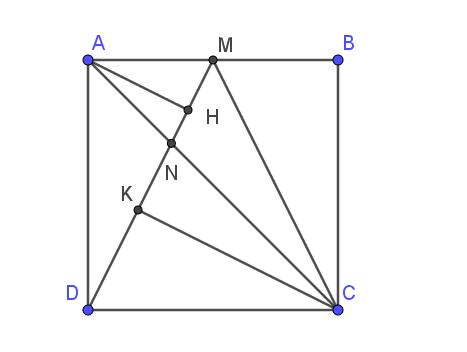
a.

$\frac{S_{DMC}}{S_{DMA}}=\frac{AD\times DC}{2}: \frac{AM\times AD}{2}=\frac{AD\times DC}{AM\times AD}=\frac{DC}{AM}=\frac{AB}{\frac{AB}{2}}=2$

Vậy diện tích tam giác DMC gấp 2  lần diện tích tam giác DMA

b.

Kẻ đường cao AH của tam giác $ADM$ và đường cao $CK$ của tam giác $DCM$
Ta có:

$2=\frac{S_{DCM}}{S_{DMA}}=\frac{CK\times MD}{2}: \frac{AH\times DM}{2}=\frac{CK}{AH}$

Suy ra:
$\frac{S_{ADN}}{S_{DNC}}=\frac{AH\times DN}{2}: \frac{CK\times DN}{2}=\frac{AH}{CK}=\frac{1}{2}$

$2\times S_{ADN}=\times S_{DNC}$

$3\times S_{ADN}=S_{DNC}+S_{ADN}=S_{ADC}=AD\times DC:2=S_{ABCD}:2$

$S_{ABCD}=3\times S_{ADN}\times 2=6\times S_{ADN}=6\times 5=30$ (cm²)

Hình vẽ:

Các tập con của {1; 2; 3; 4; 5} là:

∅; {1}; {2}; {3}; {4}; {5};

{1; 2}; {1; 3}; {1; 4}; {1; 5};

{2; 3}; {2; 4}; {2; 5}

{3; 4}; {3; 5}; {4; 5};

{1; 2; 3}; {1; 2; 4}; {1; 2; 5};

{2; 3; 4}; {2; 3; 5}; {3; 4; 5};

{1; 2; 3; 4}; {1; 2; 3; 5}; {2; 3; 4; 5};

{1; 2; 3; 4; 5}

Các tập con của {1; 2; 3; 4; 5} là:

\(\varnothing\); {1}; {2}; {3}; {4}; {5}; {1; 2}; {1; 3}; {1; 4}; {1; 5}; {2; 3}; {2; 4}; {2; 5};

{3; 4}; {3; 5}; {4; 5}; {1; 2; 3}; {1; 2; 4}; {1; 2; 5}; {1; 3; 4}; {1; 3; 5}; {1; 4; 5}

{2; 3; 4}; {2; 3; 5}; {2; 4; 5}; {3; 4; 5}; {1; 2; 3; 4}; {1; 2; 3; 5}; {1; 2; 4; 5}

{1; 3; 4; 5}; {2; 3; 4; 5}; {1; 2; 3; 4; 5}

Ai làm giúp mình với 

Giải thích các bước giải:

Chỉ thiết kế 4 luống hoa chạy suốt theo chiều rộng mảnh vườn

Khi đó chiều dài luống hoa còn là:
40 - 2 x 3 = 34 (m )
Tổng chiều rộng 4 luống hoa còn là:

80 - 5 x 3= 65 (m )
Tổng diện tích 4 luống hoa còn là:

65 x 34= 2210 (m²)

Đap So: 2210 m²

46 × 7 = ?

Lời giải:

$x^2+2xy+3y^2=6$

$\Leftrightarrow (x^2+2xy+y^2)+2y^2=6$

$\Leftrightarrow (x+y)^2+2y^2=6$
Áp dụng BĐT Bunhiacopxky:

$M^2=(x+2y)^2=[(x+y)+y]^2\leq [(x+y)^2+2y^2](1+\frac{1}{2})=6.\frac{3}{2}=9$

$\Rightarrow -3\leq M\leq 3$
Vậy $M_{\min}=-3; M_{\max}=3$.

Thời gian ô tô đi từ Đà Nẵng đến Quãng Ngải:

100 : 50 = 2 (giờ)

Thời gian xe đạp đi từ Quãng Ngải trước xe ô tô:

2 giờ + 45 phút - 15 phút = 2 giờ 30 phút = 2,5 giờ

Quãng đường xe đạp đi được trong 2,5 giờ:

10 × 2,5 = 25 (km)

Hiệu vận tốc hai xe:

50 - 10 = 40 (km/giờ)

Thời gian xe ô tô đuổi kịp xe đạp:

25 : 40 = 0,625 (giờ) = 37,5 (phút)

Hai xe gặp nhau lúc:

8 giờ 15 phút + 37,5 phút = 8 giờ 52,5 phút

Lời giải:
Vì tổng đúng là 52,42 có 2 chữ số ở phần thập phân nên số thập phân cần tìm có 2 chữ số ở phần thập phân.

Gọi số tự nhiên là a và số thập phân là b.

Ta có:

$a+b=52,42$ (1)

Khi quên dấu phẩy, bạn ấy đặt phép cộng như hai số tự nhiên thông thường nghĩa là đã gấp số thập phân ban đầu lên 100 lần.

Ta có: $a+100\times b=3757$ (2)

Lấy phép tính (2) trừ đi (1) theo vế thì:

$99\times b=3757-52,42$

$99\times b=3704,58$

$b=3704,58:99=37,42$

Số tự nhiên: $a=52,42-37,42=15$

Vậy.........

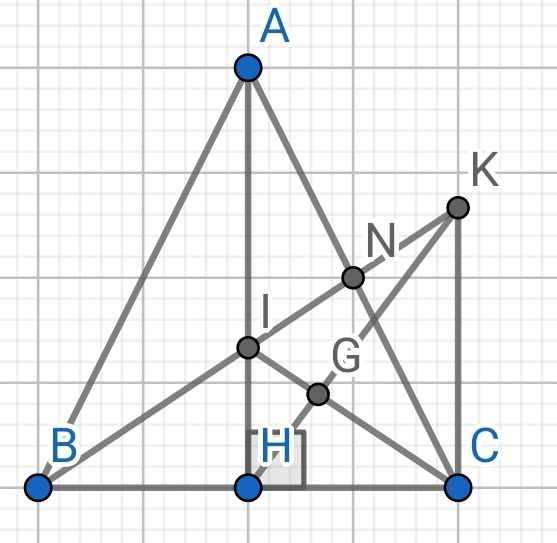
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AHC có:

AH là cạnh chung

AB = AC (cmt)

⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)

b) Do BN là đường trung tuyến của ∆ABC (gt)

⇒ N là trung điểm của AC

⇒ AN = CN

Do AH // CK (gt)

⇒ ∠IAN = ∠KCN (so le trong)

Xét ∆AIN và ∆CKN có:

∠ANI = ∠CNK (đối đỉnh)

AN = CN (cmt)

∠IAN = ∠KCN (cmt)

⇒ ∆AIN = ∆CKN (g-c-g)

⇒ NI = NK (hai cạnh tương ứng)

c) Xem lại đề. Em viết sai tùm lum

           Đây là toán nâng cao chuyên đề toán hai hiệu số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau.

                   Giải

Hiệu số học sinh của mỗi loại xe là: 30 - 16 = 14 (học sinh)

Hiệu số học sinh trong hai cách xếp xe là: 80 + 60  = 140 (học sinh)

Số xe 16 chỗ là:  140 : 14 = 10 (xe)

Số học sinh toàn trường đi du lịch là: 16 x 10 + 80 = 240 (học sinh)

Đáp số: 240 học sinh.