a) Khi m = -1, đường thẳng (d) trở thành y = -x + 7. Giao điểm của (P) và (d) là điểm A và B, khi giải hệ phương trình x^2 = -x + 7, ta có x = 1 và x = -2. Ta thấy điểm A có tọa độ (1, 2) và điểm B có tọa độ (-2, 9). Diện tích tam giác OAB được tính bằng công thức sau: S = 0.5 * |x1y2 + x2y3 + x3y1 - y1x2 - y2x3 - y3x1|, trong đó O(0,0), A(1,2), B(-2,9). Thay vào công thức ta có: S = 0.5 * |1*9 + (-2)*0 + 0*2 - 2*(-2) - 9*1 - 1*0| = 0.5 * |9 + 4 + 0 + 4 - 9 - 0| = 0.5 * 8 = 4. Vậy diện tích tam giác OAB là 4. b) Để (d) cắt (P) tại hai điểm phân biệt sao cho y1 và y2 là các số chính phương, ta cần tìm m sao cho phương trình x^2 = mx + 7 có hai nghiệm phân biệt và y1, y2 là các số chính phương. Để y1, y2 là các số chính phương, ta cần điều kiện Δ = m^2 - 4*7 = m^2 - 28 là một số chính phương. Mặt khác, để phương trình có hai nghiệm phân biệt, ta cần Δ > 0. Nên m^2 - 28 > 0 => m < -√28 hoặc m > √28. Vậy m thỏa mãn là m < -√28 hoặc m > √28.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
\(P=\frac{x+7\sqrt{x}}{x+2\sqrt{x}}=\frac{x+2\sqrt{x}+5\sqrt{x}}{x+2\sqrt{x}}=1+\frac{5\sqrt{x}}{x+2\sqrt{x}}=1+\frac{5}{\sqrt{x}+2}\)
Với $x$ là số nguyên không âm, để $P$ nguyên thì $\sqrt{x}+2$ là ước của 5.
Mà $\sqrt{x}+2\geq 2$ với mọi $x$ nguyên không âm
$\Rightarrow \sqrt{x}+2=5$
$\Rightarrow \sqrt{x}=3$
$\Rightarrow x=9$ (tm)


\(\left\{{}\begin{matrix}8x-y=6\\x^2-y=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-y-x^2+y=6+6\\8x-y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-8x=-12\\y=8x-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-8x+12=0\\y=8x-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-2\right)\left(x-6\right)=0\\y=8x-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{2;6\right\}\\y=8x-6\end{matrix}\right.\)
Khi x=2 thì \(y=8\cdot2-6=16-6=10\)
Khi x=6 thì \(y=8\cdot6-6=42\)

Thông thường thì hai nghiệm phải có quan hệ với nhau, sao biểu thức trong căn chỉ chứa \(x_1\) vậy em?

Lời giải:
$\Delta' (*) = 4^2-8(m^2+1)=8-8m^2$
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'(*) = 8-8m^2\geq 0\Leftrightarrow 1-m^2\geq 0$
$\Leftrightarrow -1\leq m\leq 1$
Áp dụng định lý Viet:
$x_1+x_2=1$
$x_1x_2=\frac{m^2+1}{8}$
Khi đó:
$x_1^4-x_2^4=x_1^3-x_2^3$
$\Leftrightarrow (x_1^2-x_2^2)(x_1^2+x_2^2)=(x_1-x_2)(x_1^2+x_1x_2+x_2^2)$
$\Leftrightarrow (x_1-x_2)[(x_1+x_2)(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$
$\Leftrightarrow (x_1-x_2)[1(x_1^2+x_2^2)-(x_1^2+x_1x_2+x_2^2)]=0$
$\Leftrightarrow (x_1-x_2)(-x_1x_2)=0$
$\Leftrightarrow (x_1-x_2).\frac{-(m^2+1)}{8}=0$
$\Leftrightarrow x_1-x_2=0$ (do $m^2+1\geq 1>0$ với mọi $m$ nên số này khác 0)
$\Leftrightarrow x_1=x_2$
Kết hợp $x_1+x_2=1$
$\Rightarrow x_1=x_2=\frac{1}{2}$
$\frac{m^2+1}{8}=x_1x_2=\frac{1}{4}$
$\Leftrightarrow m^2+1=2$
$\Leftrightarrow m^2=1\Leftrightarrow m=\pm 1$ (tm)

Lời giải:
$BC=\sqrt{AB^2+AC^2}=\sqrt{18^2+24^2}=30$ (cm) - áp dụng định lý Pitago.
Nửa chu vi tam giác: $p=(AB+BC+AC):2=(18+24+30):2=36$ (cm)
Diện tích: $S=AB.AC:2=18.24:2=216$ (cm2)
Áp dụng công thức:
$S=pr$ với $r$ là bán kính đường tròn nội tiếp tam giác.
$r=\frac{S}{p}=\frac{216}{36}=6$ (cm)

Bài 1:
1: Thay x=2025 vào A, ta được:
\(A=\dfrac{2025+5}{\sqrt{2025}-2}=\dfrac{2030}{43}\)
2: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-2\left(\sqrt{x}-2\right)-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
3: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\cdot\dfrac{x+5}{\sqrt{x}-2}=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\dfrac{x-4+9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4>=2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=\sqrt{9}=3\)
=>x=1(nhận)
Bài 3:
1: Khi m=-2 thì phương trình sẽ trở thành:
\(x^2+2\cdot\left(-2\right)\cdot x-2-3=0\)
=>\(x^2-4x-5=0\)
=>(x-5)(x+1)=0
=>\(\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
2: \(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(m-3\right)\)
\(=4m^2-4m+12=4m^2-4m+1+11=\left(2m-1\right)^2+11>0\forall m\)
=>Phương trình luôn có 2 nghiệm phân biệt
Theo vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2m\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(x_1^2+x_1x_2-2x_2^2=3\left(x_1-x_2\right)\)
=>\(x_1^2+2x_1x_2-x_1x_2-2x_2^2=3\left(x_1-x_2\right)\)
=>\(x_1\left(x_1+2x_2\right)-x_2\left(x_1+2x_2\right)-3\left(x_1-x_2\right)=0\)
=>\(\left(x_1-x_2\right)\left(x_1+2x_2-3\right)=0\)
=>\(\left[{}\begin{matrix}x_1=x_2\\x_1+2x_2=3\end{matrix}\right.\)
TH1: \(x_1=x_2\)
mà \(x_1+x_2=-2m\)
nên \(x_1=x_2=-m\)
\(x_1x_2=m-3\)
=>\(\left(-m\right)\cdot\left(-m\right)=m-3\)
=>\(m^2-m+3=0\)
=>\(\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}=0\)(vô lý)
TH2: \(x_1+2x_2=3\)
mà \(x_1+x_2=-2m\)
nên \(x_2=3-\left(-2m\right)=2m+3\)
=>\(x_1=-2m-x_2=-2m-\left(2m+3\right)=-4m-3\)
\(x_1x_2=m-3\)
=>\(\left(2m+3\right)\left(-4m-3\right)=m-3\)
=>\(-8m^2-6m-12m-9=m-3\)
=>\(-8m^2-18m-9-m+3=0\)
=>\(-8m^2-19m-6=0\)
=>\(\left[{}\begin{matrix}m=-\dfrac{3}{8}\\m=-2\end{matrix}\right.\)

a: Xét tứ giác EAOD có \(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
nên EAOD là tứ giác nội tiếp
b: Xét (O) có
EA,ED là các tiếp tuyến
Do đó: EA=ED
=>E nằm trên đường trung trực của AD(1)
ta có: OA=OD
=>O nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra OE là đường trung trực của AD
=>OE\(\perp\)AD tại H
Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét ΔEAB vuông tại A có AK là đường cao
nên \(EK\cdot EB=EA^2\left(3\right)\)
Xét ΔEAO vuông tại A có AH là đường cao
nên \(EH\cdot EO=EA^2\left(4\right)\)
Từ (3),(4) suy ra \(EK\cdot EB=EH\cdot EO\)

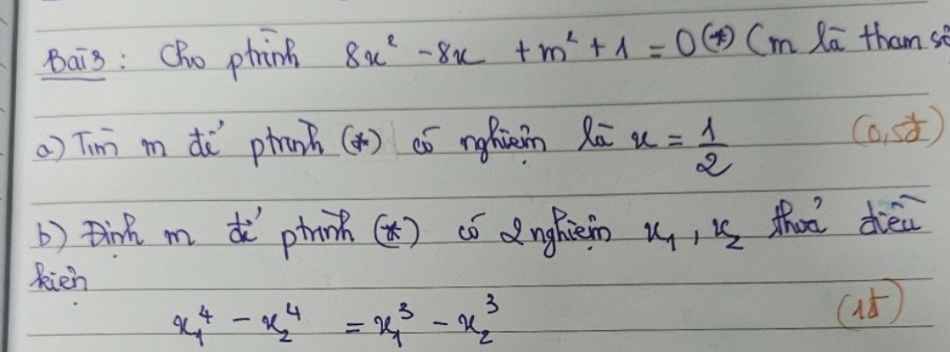

Bạn nên viết lại đề cho rõ ràng để mọi người đọc hiểu và hỗ trợ nhanh hơn nhé.