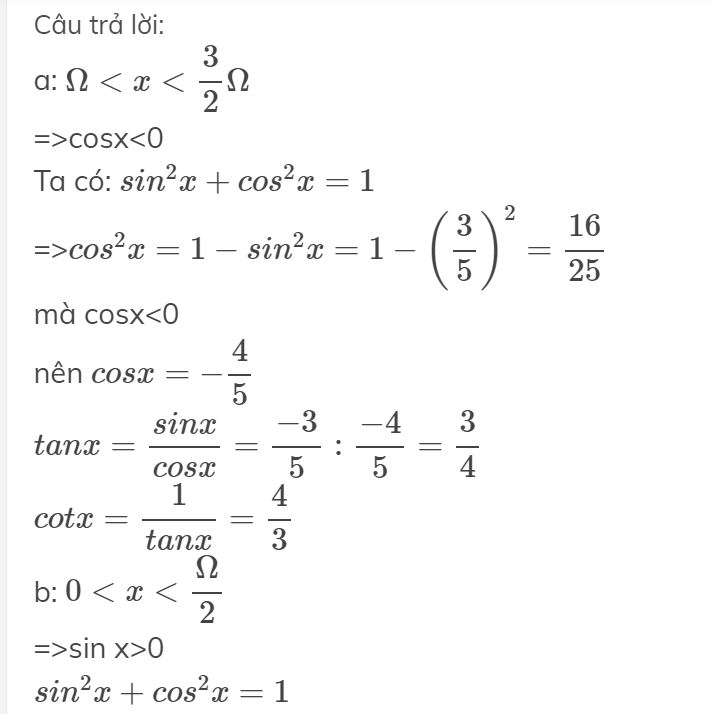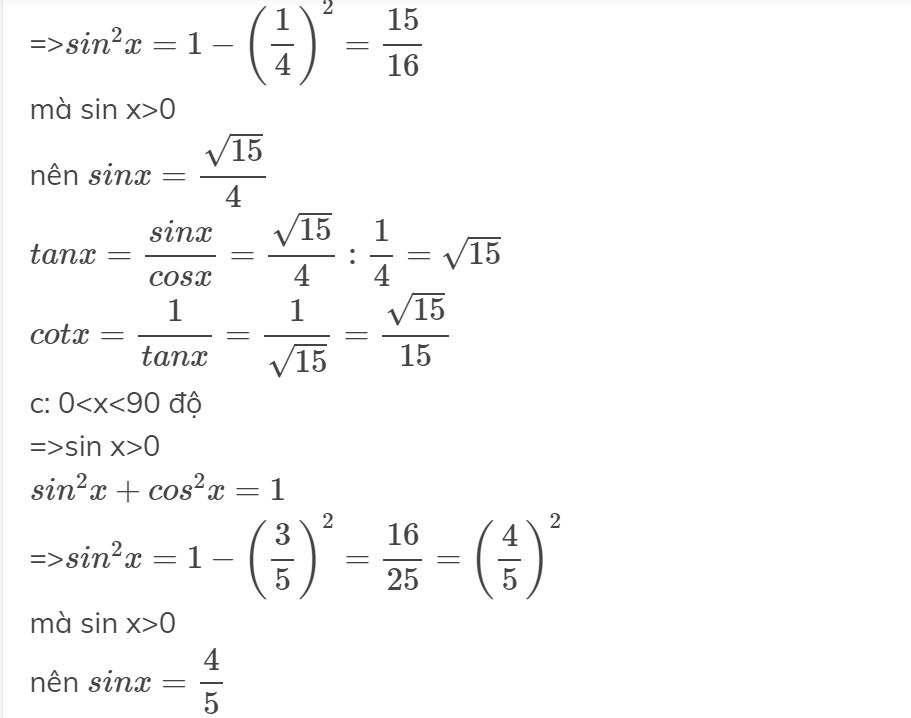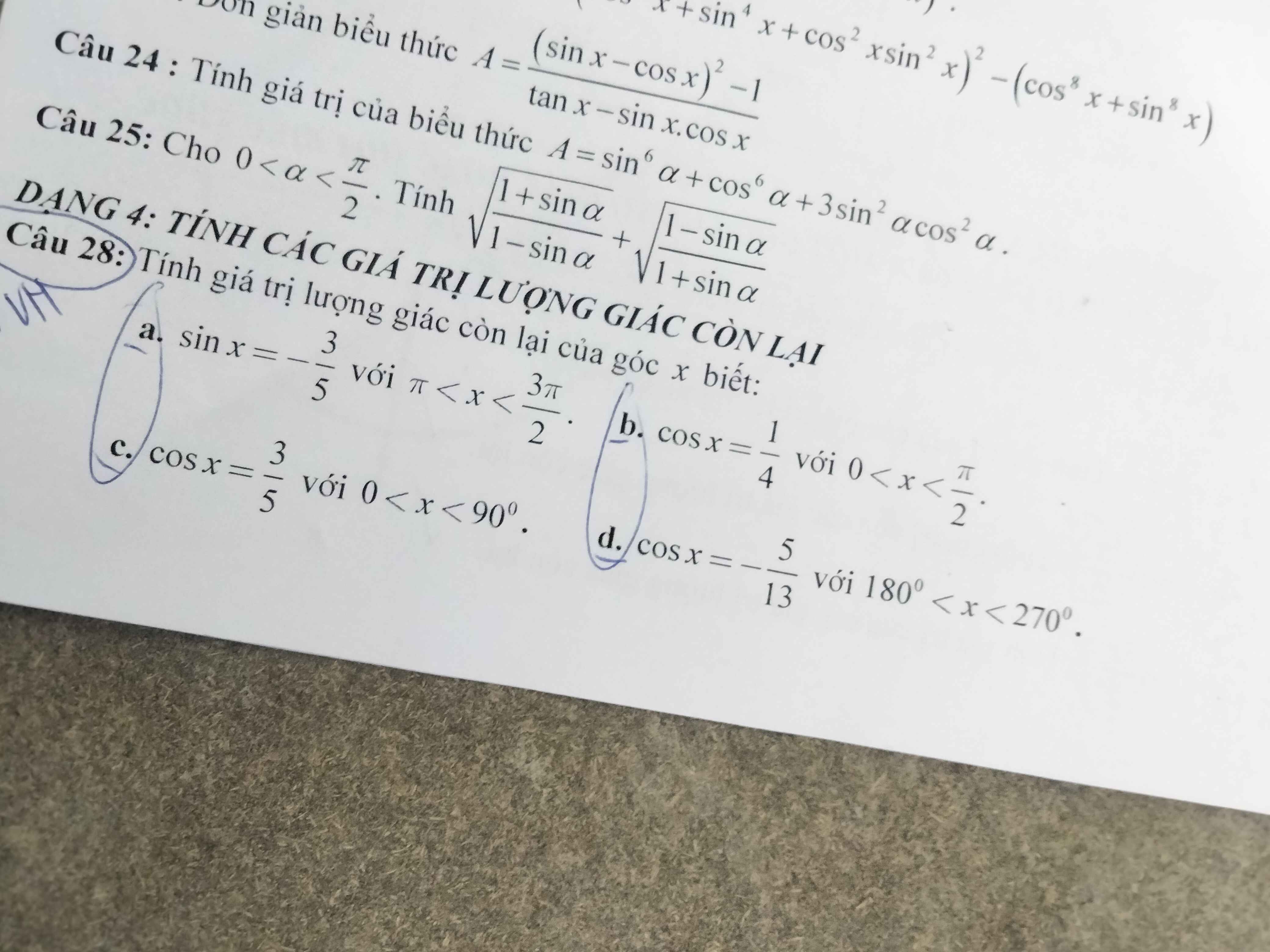Cho tập hợp X={0;1;2;3;5;6;8;9}. Số lập được không vượt quá 200 và không có chữ số xuất hiện quá 1 lần
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(S_1=2\cdot1^2-4\cdot1=2-4=-2\)
=>\(u_1=-2\)
\(S_2=2\cdot2^2-4\cdot2=8-8=0\)
=>\(u_1+u_2=0\)
=>\(u_2=-u_1=2\)
=>Đúng
b: \(S_{n}-S_{n-1}=\left(2n^2-4n\right)-\left\lbrack2\cdot\left(n-1\right)^2-4\cdot\left(n-1\right)\right\rbrack\)
\(=2n^2-4n-\left\lbrack2n^2-4n+2-4n+4\right\rbrack=2n^2-4n-\left(2n^2-8n+6\right)\)
\(=2n^2-4n-2n^2+8n-6=4n-6\)
=>Đúng
c: \(S_{n}-S_{n-1}=\left(u_1+u_2+\cdots+u_{n}\right)-\left(u_1+u_2+\cdots+u_{n-1}\right)=u_{n}\)
=>\(u_{n}=4n-6\)
=>\(u_{n+1}=4\left(n+1\right)-6=4n+4-6=4n-2\)
=>\(u_{n+1}-u_{n}=4n-2-\left(4n-6\right)=4n-2-4n+6=4\)
=>Công sai là 4
=>Sai
d: \(u_2+u_4+u_6+\cdots+u_{100}\)
\(=\left(4\cdot2-6\right)+\left(4\cdot4-6\right)+\cdots+\left(4\cdot100-6\right)\)
=4(2+4+...+100)-6*50
\(=4\cdot2\left(1+2+\cdots+50\right)-300=8\cdot\frac{50\cdot51}{2}-300=4\cdot50\cdot51-300\)
=200*51-300
=9900
=>Sai

a) Trong mặt phẳng (SAC), gọi I là giao điểm của AO và MN. Khi đó vì \(MN\subset\left(BMN\right)\) nên I chính là giao điểm của (BMN) và SO.
b) Ta có \(I\in SO\subset\left(SBD\right)\) nên \(I\in\left(SBD\right)\). Trong mặt phẳng (SBD), gọi K là giao điểm của BI và SD. Khi đó vì \(K\in BI\subset\left(BMN\right)\) nên K chính là giao điểm của (BMN) và SD.
a: Trong mp(SAC), gọi K là giao điểm của MN với SO
mà MN\(\in\left(BMN\right)\)
nên \(K=SO\cap\left(BMN\right)\)
b: Vì K là giao của MN và SO
mà \(MN\in\left(BMN\right);SO\in\left(SBD\right)\)
nên \(K\in\left(BMN\right)\cap\left(SBD\right)\)
mà \(B\in\left(BMN\right)\cap\left(SBD\right)\)
nên \(\left(BMN\right)\cap\left(SBD\right)=BK\)
Gọi E là giao điểm của BK với SD
=>K là giao điểm của SD với (BMN)

Có \(u_0=\dfrac{1}{2.0^2-3}=-\dfrac{1}{3};u_1=\dfrac{1}{2.1^2-3}=-1\)
Ta có \(u_{n+1}=\dfrac{1}{2\left(n+1\right)^2-3}< \dfrac{1}{2n^2-3}=u_n\) với \(n\ge2\)
Khi đó \(\left\{u_n\right\}\) là dãy giảm với \(n\ge2\). Do đó \(u_n\le u_2=\dfrac{1}{2.2^2-3}=\dfrac{1}{5}\) hay \(\left\{u_n\right\}\) bị chặn trên bởi \(\dfrac{1}{5}\).
Mặt khác, với \(n\ge2\) thì \(u_n>0\). Do đó \(\left\{u_n\right\}\) bị chặn dưới bởi \(-1\).

Nếu \(n\) chẵn thì đpcm trở thành \(\dfrac{3n+1}{4n-1}\le\dfrac{3n+4}{4n-1}\) \(\Leftrightarrow3n+1\le3n+4\) \(\Leftrightarrow1\le4\), luôn đúng.
Nếu \(n\) lẻ thì đpcm thành \(\dfrac{3n-1}{4n+1}\le\dfrac{3n+4}{4n-1}\)
\(\Leftrightarrow\left(3n-1\right)\left(4n-1\right)\le\left(4n+1\right)\left(3n+4\right)\)
\(\Leftrightarrow12n^2-3n-4n+1\le12n^2+16n+3n+4\)
\(\Leftrightarrow26n+3\ge0\) (luôn đúng)
Vậy với mọi \(n\inℕ^∗\) thì \(\dfrac{3n+\left(-1\right)^n}{4n-\left(-1\right)^n}\le\dfrac{3n+4}{4n-1}\)

Câu 3:
\(u_1=\dfrac{2\cdot1+1}{1+2}=\dfrac{3}{3}=1\)
\(u_4=\dfrac{2\cdot4+1}{4+2}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(u_5=\dfrac{2\cdot5+1}{5+2}=\dfrac{11}{7}\)
Câu 2:
\(u_n=u_1+\left(n-1\right)\cdot d\)
=>\(-3\left(n-1\right)+4=-41\)
=>-3(n-1)=-45
=>n-1=15
=>n=16
Câu 1:
Tổng của 50 số hạng đầu là 5150
=>\(\dfrac{n\cdot\left[2\cdot u_1+\left(n-1\right)\cdot d\right]}{2}=5150\)
=>\(\dfrac{50\left(2\cdot5+\left(50-1\right)\cdot d\right)}{2}=5150\)
=>\(25\left(10+49d\right)=5150\)
=>49d+10=206
=>49d=196
=>d=4
\(u_{10}=u_1+9d=5+9\cdot4=5+36=41\)

Câu 1:
-2;x;-18;y là cấp số nhân
=>\(\left\{{}\begin{matrix}x^2=\left(-2\right)\cdot\left(-18\right)\\\left(-18\right)^2=x\cdot y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=36\\xy=324\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=\dfrac{324}{6}=54\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=\dfrac{324}{-6}=-54\end{matrix}\right.\end{matrix}\right.\)
=>Chọn C
Câu 2:
\(u_4=u_2\cdot q^2\)
=>\(4q^2=9\)
=>\(q^2=\dfrac{9}{4}=\left(\dfrac{3}{2}\right)^2\)
=>\(\left[{}\begin{matrix}q=\dfrac{3}{2}\\q=-\dfrac{3}{2}\end{matrix}\right.\)
TH1: q=3/2
\(u_2=q\cdot u_1\)
=>\(u_1=\dfrac{u_2}{q}=4:\dfrac{3}{2}=4\cdot\dfrac{2}{3}=\dfrac{8}{3}\)
\(u_5=u_1\cdot q^4=\dfrac{8}{3}\cdot\left(\dfrac{3}{2}\right)^4=\dfrac{8}{3}\cdot\dfrac{81}{16}=\dfrac{27}{2}\)
\(u_8=u_1\cdot q^7=\dfrac{8}{3}\cdot\left(\dfrac{3}{2}\right)^7=\dfrac{2^3}{3}\cdot\dfrac{3^7}{2^7}=\dfrac{3^6}{2^4}=\dfrac{729}{16}\)
TH2: q=-3/2
\(u_1=\dfrac{u_2}{q}=4:\dfrac{-3}{2}=4\cdot\dfrac{-2}{3}=-\dfrac{8}{3}\)
\(u_5=u_1\cdot q^4=-\dfrac{8}{3}\cdot\left(-\dfrac{3}{2}\right)^4=-\dfrac{8}{3}\cdot\dfrac{81}{16}=\dfrac{-27}{2}\)
\(u_8=u_1\cdot q^7=\dfrac{-8}{3}\cdot\left(-\dfrac{3}{2}\right)^7=\dfrac{-2^3}{3}\cdot\dfrac{\left(-3\right)^7}{2^7}=\dfrac{2^3}{3}\cdot\dfrac{3^7}{2^7}=\dfrac{3^4}{2^4}=\dfrac{81}{16}\)
Câu 3:
\(\left\{{}\begin{matrix}u_1+u_5=51\\u_2+u_6=102\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1\cdot q^4=51\\u_1\cdot q+u_1\cdot q^5=102\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q^4=51\\q\left(u_1+u_1\cdot q^4\right)=102\end{matrix}\right.\Leftrightarrow q=2\)
\(u_1+u_5=51\)
=>\(u_1\left(1+q^4\right)=51\)
=>\(u_1=\dfrac{51}{2^4+1}=\dfrac{51}{17}=3\)
\(u_4=u_1\cdot q^3=3\cdot2^3=24\)
\(u_{12}=u_1\cdot q^{11}=3\cdot2^{11}=6144\)

Câu 1: \(u_4=u_1+3k\)
=>\(3k=\dfrac{3}{8}-3=\dfrac{3}{8}-\dfrac{24}{8}=-\dfrac{21}{8}\)
=>\(k=-\dfrac{7}{8}\)
\(u_7=u_1+6k=3+6\cdot\dfrac{-7}{8}=3-\dfrac{42}{8}=\dfrac{24-42}{8}=-\dfrac{18}{8}=-\dfrac{9}{4}\)
Câu 2:
\(\dfrac{u_5}{u_8}=8\)
=>\(\dfrac{u_1\cdot q^4}{u_1\cdot q^7}=8\)
=>\(\dfrac{1}{q^3}=8\)
=>\(q=\dfrac{1}{2}\)
\(u_{12}=u_1\cdot q^{11}=12\cdot\left(\dfrac{1}{2}\right)^{11}=\dfrac{12}{2^{11}}=\dfrac{3}{2^9}\)
Câu 3:
Tổng của 5 số hạng đầu là:
\(S_5=\dfrac{u_1\cdot\left(1-q^5\right)}{1-q}=\dfrac{2\cdot\left(1-4^5\right)}{1-4}=682\)
=>Chọn D

Câu 25:
\(0< \alpha< \dfrac{\Omega}{2}\)
=>\(0< sin\alpha< 1;0< cos\alpha< 1\)
\(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\)
\(=\dfrac{1+sin\alpha+1-sin\alpha}{cos\alpha}=\dfrac{2}{cos\alpha}\)
Câu 28: