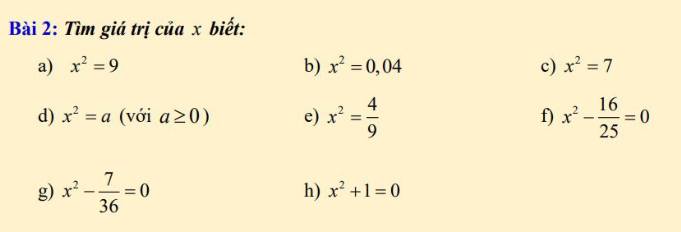d) \(x^2=a\left(a\ge0\right)\)

\(\Rightarrow x=\sqrt{a}\)

e) \(x^2=\dfrac{4}{9}\)

\(\Rightarrow x^2=\left(\pm\dfrac{2}{3}\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)

f) \(x^2-\dfrac{16}{25}=0\)

\(\Rightarrow x^2=\dfrac{16}{25}\)

\(\Rightarrow x^2=\left(\pm\dfrac{4}{5}\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)

g) \(x^2-\dfrac{7}{36}=0\)

\(\Rightarrow x^2=\dfrac{7}{36}\)

\(\Rightarrow x^2=\left(\pm\sqrt{\dfrac{7}{36}}\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{7}{36}}\\x=-\sqrt{\dfrac{7}{36}}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{7}}{6}\\x=-\dfrac{\sqrt{7}}{6}\end{matrix}\right.\)

h) Ta có: \(x^2\ge0\forall x\)

\(\Rightarrow x^2+1\ge1>0\forall x\)

mà \(x^2+1=0\)

nên không tìm được giá trị nào của x thoả mãn đề bài.

a)M đã không quan tâm đến các môn học khác

b)Nếu là bạn của M, em sẽ khuyên M phải tập trung nhiều môn học quan trọng khác, đừng quá quan tâm vào môn Tiếng Anh

Bài 3

a) 5/7 - x = 6/5

x = 5/7 - 6/5

x = -17/35

b) 4/5 x - 2/3 = 1 1/3

4/5 x - 2/3 = 4/3

4/5 x = 4/3 + 2/3

4/5 x = 2

x = 2 : 4/5 

x = 5/2

Ta thấy: \(3\left|x+y\right|\ge0\forall x;y\)

              \(10\left|y+\dfrac{2}{3}\right|\ge0\forall y\)

\(\Rightarrow3\left|x+y\right|+10\left|y+\dfrac{2}{3}\right|\ge0\forall x;y\)

Mà: \(3\left|x+y\right|+10\left|y+\dfrac{2}{3}\right|\le0\)

nên: \(\left\{{}\begin{matrix}x+y=0\\y+\dfrac{2}{3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-y\\y=-\dfrac{2}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{2}{3}\end{matrix}\right.\)

Vậy \(x=\dfrac{2}{3};y=-\dfrac{2}{3}\).

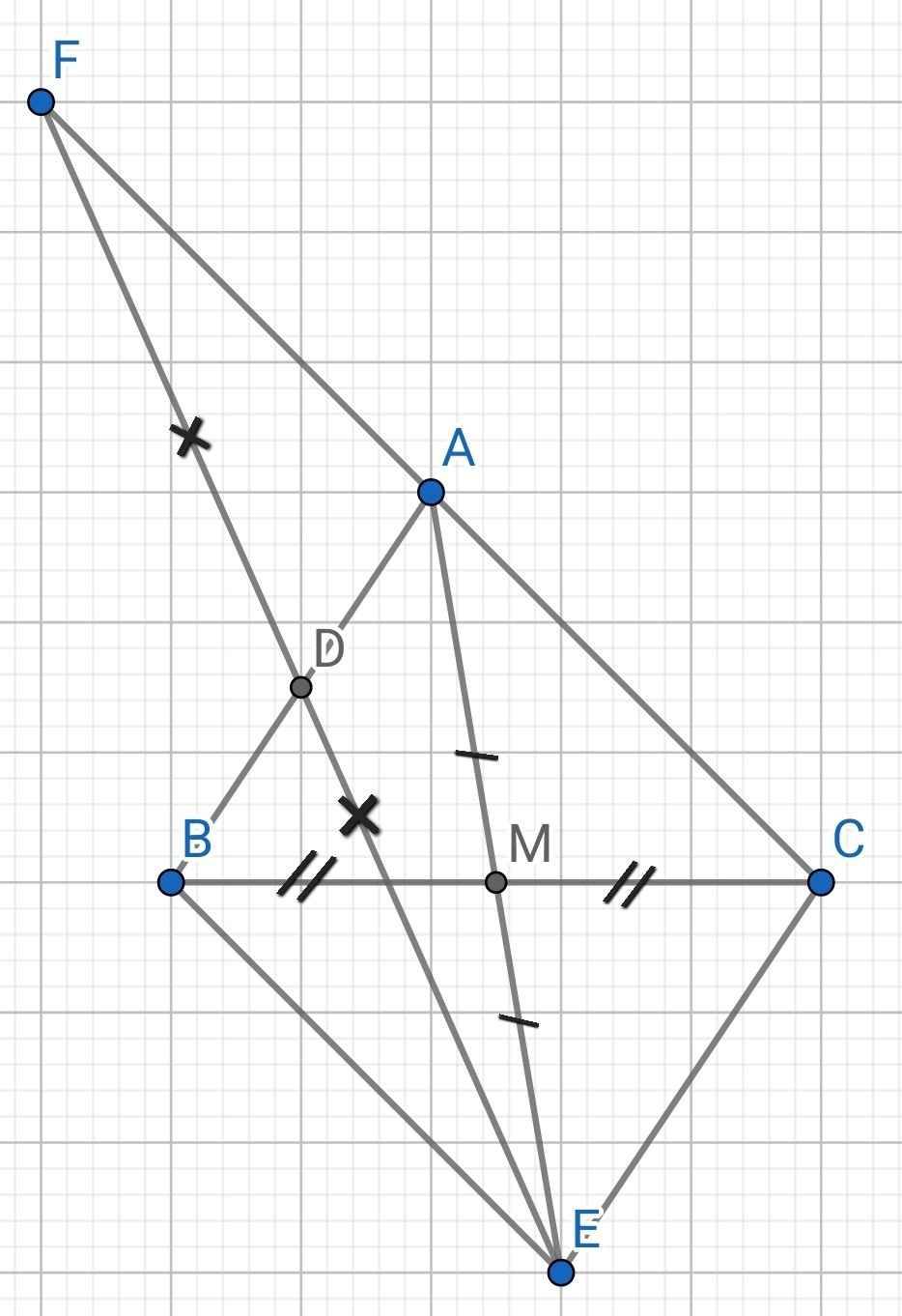 a) Xét ∆AMC và ∆EMB có:

AM = EM (gt)

MC = MB (gt)

∠AMC = ∠EMB (đối đỉnh)

⇒ ∆AMC = ∆EMB (c-g-c)

⇒ AC = BE (hai cạnh tương ứng)

b) Do D là trung điểm AB (gt)

⇒ AD = BD

Xét ∆ADF và ∆BDE có:

AD = BD (cmt)

FD = DE (gt)

∠ADF = ∠BDE (đối đỉnh)

⇒ ∆ADF = ∆BDE (c-g-c)

⇒ AF = BE (hai cạnh tương ứng)

Mà BE = AC (cmt)

⇒ AC = AF

bình phương của 13 là 169

\(13^2=13.13=169\)