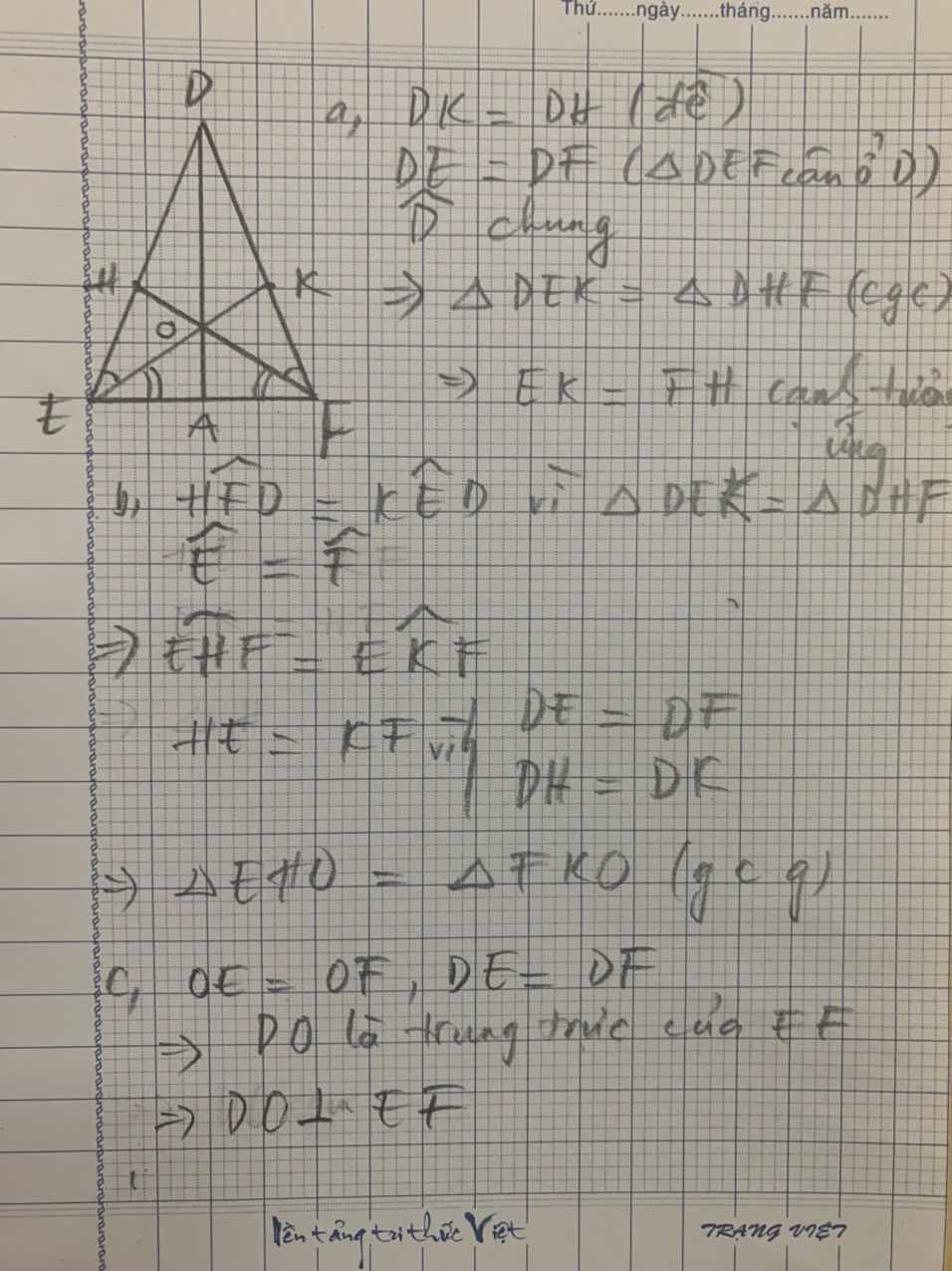2023-1/2*(1+2)-1/3*(1+2+3)-1/4*(1+2+3+4)-...-1/2022*(1+2+3+4+...+2022)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có HE = DE - DH
KF = DF - DK
Mà DH = DK (gt)
và DE = DF ( △DEF cân tại D )
⇒ HE = KF
Xét △HEF và △KFE có:
HE = KF (cmt)
\(\widehat{HEF}\) = \(\widehat{KFE}\) ( △DEF cân tại D )
EF là cạnh chung
⇒ △HEF = △KFE ( c-g-c )
⇒ FH = EK ( 2 cạnh tương ứng )
b) Theo câu a có △HEF = △KFE
⇒ \(\widehat{OEF}\) = \(\widehat{OFE}\) ( 2 góc tương ứng )
Xét △OEF có:
\(\widehat{OEF}\) = \(\widehat{OFE}\) (cmt)
⇒ △OEF cân tại O
⇒ OE = OF
Ta có: \(\widehat{HEF}\) - \(\widehat{OEF}\) = \(\widehat{HEO}\)
và \(\widehat{KFE}\) - \(\widehat{OFE}\) = \(\widehat{KFO}\)
Lại có: \(\widehat{HEF}\) = \(\widehat{KFE}\) ; \(\widehat{OEF}\) = \(\widehat{OFE}\) (cmt)
⇒ \(\widehat{HEO}\) = \(\widehat{KFO}\)
Xét △HEO và △KFO có:
OE = OF (cmt)
\(\widehat{HEO}\) = \(\widehat{KFO}\) (cmt)
HE = KF ( theo a)
⇒ △HEO = △KFO (c-g-c)
c) Gọi A là giao điểm của DO và EF
Theo câu b có △HEO = △KFO
⇒ HO = OK ( 2 cạnh tương ứng )
Xét △HDO và △KDO có:
DH = DK (gt)
HO = OK (cmt)
DO là cạnh chung
⇒ △HDO = △KDO (c-c-c)
Xét △DCE và △DCF có:
DE = DF (△DEF cân tại D )
\(\widehat{EDC}\) = \(\widehat{FDC}\) (cmt)
DC là cạnh chung
⇒ △DCE = △DEF (c-g-c)
⇒ \(\widehat{DCE}\) = \(\widehat{DEF}\) ( 2 góc tương ứng )
Mà \(\widehat{DCE}\) = \(\widehat{DCF}\) = \(\dfrac{180^0}{2}\) = 900 hay DO \(\perp\) EF

ĐKXĐ : \(x\ne2\)
Ta có HĐT sau (a - b)(a + b) = a2 - ab + ab - b2 = a2 - b2
Áp dụng vào bài toán ta có:
x4 + 3 = (x4 - 16) + 19
= [(x2)2 - 42] + 19
= (x2 - 4)(x2 + 4) + 19
= (x - 2)(x + 2)(x2 + 4) + 19
Từ đó \(A=\dfrac{x^2+3}{x-2}=\dfrac{\left(x-2\right).\left(x+2\right).\left(x^2+4\right)+19}{x-2}\)
\(=\left(x+2\right).\left(x^2+4\right)+\dfrac{19}{x-2}\)
Do \(x\inℤ\) nên \(A\inℤ\Leftrightarrow19⋮x-2\)
\(\Leftrightarrow x-2\inƯ\left(19\right)=\left\{1;-1;19;-19\right\}\)
hay \(x\in\left\{3;1;21;-17\right\}\)

Gọi số tự nhiên đó là a
vì a ⋮ 3; a \(⋮\) 4 ⇒ a \(\in\) BC(3; 4)
3 = 3
4 = 22
⇒ BCNN( 3; 4) = 3.22 = 12
⇒ a \(\in\) A = { a = 12k/ k \(\in\)N}

a.
$7x-2y=5x-3y$
$\Leftrightarrow 2x=-y$. Thay vào điều kiện số 2 ta có:
$-y+3y=20$
$2y=20$
$\Rightarrow y=10$.
$x=\frac{-y}{2}=\frac{-10}{2}=-5$
b.
$2x=3y\Rightarrow \frac{x}{3}=\frac{y}{2}$
$3y=4z-2y\Rightarrow 5y=4z\Rightarrow \frac{y}{4}=\frac{z}{5}$
$\Rightarrow \frac{x}{6}=\frac{y}{4}=\frac{z}{5}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{6}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{6+4+5}=\frac{45}{15}=3$
$\Rightarrow x=6.3=18; y=4.3=12; z=5.3=15$

a, Vì trong hộp có 1 viên bi màu đỏ nên có 1 kết quả thuận lợi cho biến cố: Viên bi lấy ra có màu đỏ
vậy xác xuất cho biến cố trên là: \(\dfrac{1}{100}\)
b, Vì trong hộp có 99 viên bi màu xanh nên có 99 kết quả thuận lợi cho biến cố: Viên bi lấy ra có màu xanh
Vậy xác xuất cho biến cố trên là: \(\dfrac{99}{100}\)

F(1) = -5 m . 1 + 10 = 5 ⇒ -5m + 10 = 5 ⇒ 5m = 10 - 5
⇒ 5m = 5 ⇒ m = 1
F(2) = -5m. 2 + 10 = 15 ⇒ -10m = 15- 10 ⇒ -10m = 5 ⇒ m = -1/2
F(3) = -5.m .3 + 10 = 10 ⇒ - 15m = 0 ⇒ m = 0