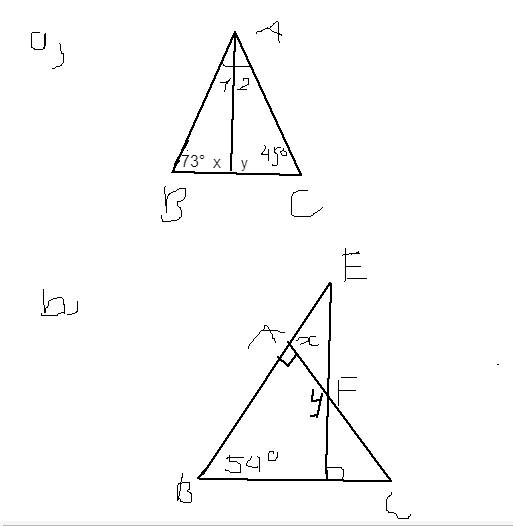
Tìm x và y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{5}{18}+\dfrac{7}{15}-\dfrac{7}{21}+\left(\dfrac{-10}{36}\right)+\dfrac{8}{15}+\dfrac{1}{3}-\dfrac{4}{9}\\ =\left(\dfrac{5}{18}+\dfrac{-10}{36}\right)+\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+\left(\dfrac{-7}{21}+\dfrac{1}{3}\right)-\dfrac{4}{9} \\ =0+1+0-\dfrac{4}{9}=\dfrac{5}{9}\)

b, Gọi ba số cần tìm lần lượt là:
\(x;y;z\) theo bài ra ta có:
\(\dfrac{x}{4}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{6}\);
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{z}{6}\) = \(\dfrac{x}{4}\) = \(\dfrac{z-x}{6-4}\) = \(\dfrac{4}{2}\) = 2
z = 2 x 6 = 12
\(x\) = 2 x 4 = 8
\(\dfrac{y}{5}\) = 2 ⇒ y = 2 x 5 = 10
Vậy \(x\) = 8; y = 10; z = 12
a, Gọi ba số cần tìm lần lượt là: \(x\); y; z
Theo bài ra ta có: \(\dfrac{x}{3}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{7}\); z - 2\(x\) = 11
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}\) = \(\dfrac{2x}{6}\) = \(\dfrac{z}{7}\) = \(\dfrac{z-2x}{7-6}\) = \(\dfrac{4}{1}\) = 4
\(x\) = 4x3 = 12; z = 4 x 7 = 28
\(\dfrac{y}{5}\) = 4 ⇒ y = 4x5 =20
Vậy \(x\) = 12; y = 20; z = 28

a)Quãng đường hai người đi trong \(t=40min=\dfrac{2}{3}h\) là:
Người thứ nhất: \(S_1=v_1t=15\cdot\dfrac{2}{3}=10km\)
Người thứ hai: \(S_2=v_2t=12\cdot\dfrac{2}{3}=8km\)
b)Thời gian người thứ hai đi: \(t_2=\dfrac{S_2}{v_2}=\dfrac{18}{12}=1,5h\)
Để đến B cùng lúc, thời gian còn lại để người thứ nhất đi:
\(\Delta t_1=1,5-\dfrac{40}{60}-\dfrac{23}{60}=0,45h\)
Quãng đường còn lại người thứ nhất cần đi:
\(\Delta S_1=18-\dfrac{40}{60}\cdot15=8km\)
Vận tốc người thứ nhất cần đạt: \(v_1'=\dfrac{\Delta S_1}{\Delta t_1}=\dfrac{8}{0,45}=\dfrac{160}{9}\approx17,8km/h\)

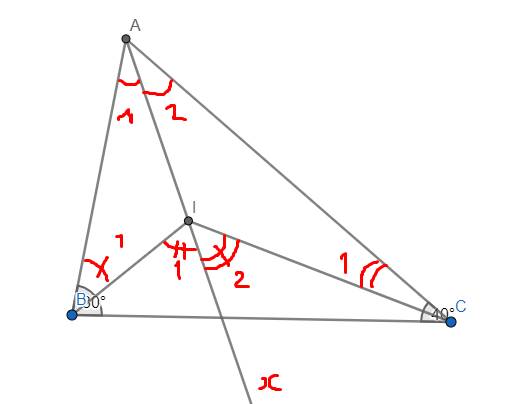
Ta có \(\widehat{I_1}=\widehat{A_1}+\widehat{B_1}\) và \(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\)
\(\Rightarrow\widehat{BIC}=\widehat{I_1}+\widehat{I_2}\)
\(=\left(\widehat{A_1}+\widehat{A_2}\right)+\left(\widehat{B_1}+\widehat{C_1}\right)\)
\(=\widehat{BAC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(80^o+40^o\right)+\dfrac{80^o+40^o}{2}\)
\(=120^o\)
Vậy \(\widehat{BIC}=120^o\)
B1: Cho tam giác ABC có B=80, C=40 độ. Tia phân giác của góc B cắt AC tại D. Tính ADB.
B2: Cho ta giác ABC có B-C=20 độ. Đường phân giác AD của góc A cắt BC tại D. Tính ADB và ADC.
B3: Cho hình vẽ tính ACB

=> Mk tự làm, có gì sai sót mg bạn thông cảm (còn nhiều bài lắm)
This is my idol. She is JENNIE. She comes from Korean. She is 27 years old. She works in YG ENT. She is a member of BLACKPINK and she is main rapper in BLACKPINK. She started working as a YG ENT trainess at the age of 16. She sings very well. Her favourite colour is pink. She is so cute.
B2: about WONYOUNG
My idol is Wonyoung. Her full name is Jang Wonyoung. She is 19 years old. She is Korean. She was a member of IZ*ONE from 2016 to 2020, and she is a member of IVE from 2021 to present. She is visual of group. The company she works is Starship ENT. She doesn't have a good voice but I like her

Lời giải:
$S=\frac{1}{2^2}-\frac{1}{2^4}+\frac{1}{2^6}-....+\frac{1}{2^{2002}}-\frac{1}{2^{2004}}$
$2^2S=1-\frac{1}{2^2}+\frac{1}{2^4}-....+\frac{1}{2^{2000}}-\frac{1}{2^{2002}}$
$\Rightarrow S+2^2S=1-\frac{1}{2^{2004}}<1$
$\Rightarrow 5S< 1$
$\Rightarrow S< \frac{1}{5}$
Hay $S<0,2$
a) Ta có:
∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠BAC = 180⁰ - ∠B - ∠C
= 180⁰ - 73⁰ - 45⁰ = 62⁰
⇒ ∠A₁ = ∠A₂ = 62⁰ : 2
= 21⁰
⇒ x = 180⁰ - ∠B - ∠A₁
= 180⁰ - 73⁰ - 31⁰
= 76⁰
y = 180⁰ - ∠C - ∠A₂
= 180⁰ - 45⁰ - 31⁰
= 104⁰
b)
Ta có:
∠BAC + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠C = 180⁰ - ∠BAC - ∠B
= 180⁰ - 54⁰ - 90⁰
= 36⁰
Ta có:
∠C + ∠CFH + ∠CHF = 180⁰ (tổng ba góc trong ∆CHF)
⇒ ∠CFH = 180⁰ - ∠C - ∠CHF
= 180⁰ - 36⁰ - 90⁰
= 54⁰
Ta có:
y + ∠CFH = 180⁰ (kề bù)
⇒ y = 180⁰ - 54⁰
= 126⁰
x là góc nào em?