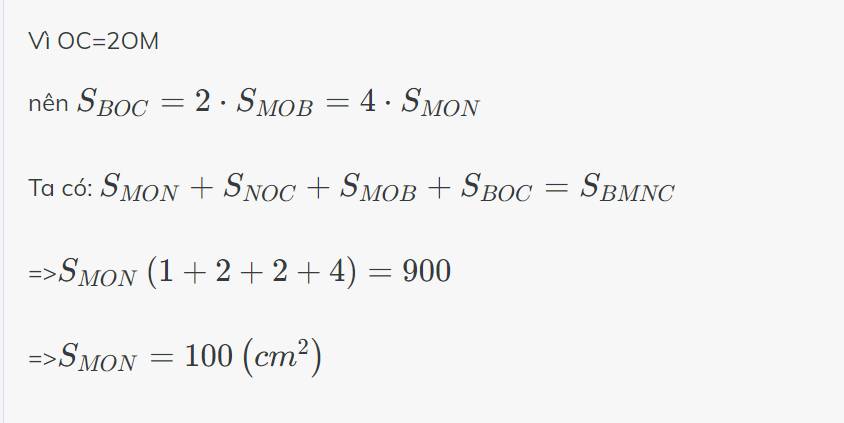Olm chào em, nếu tài khoản hết vip em tiếp tục gia hạn vip em nhé. Nếu muốn hưởng quyền lợi đặc biệt hơn thì em liên hệ với cô qua zalo để được nhận thêm quà khi gia hạn vip em nhé

Zalo của cô số: 0385 168 017 

Có nhé bạn!

5628dm=562,8m

0,2kg=200g

3 giờ 6 phút = 3,1 giờ

0,48m=48/100m

5628 dm = 562,8 m

0,2 kg = 200 g

3 giờ 6 phút = 3,1 giờ

0,48 m = 0,48 m

Câu 1:

\(B=\frac{2x-3}{x-3\sqrt x}-\frac{1}{\sqrt x}=\frac{2x-3}{\sqrt x(\sqrt x-3)}-\frac{\sqrt x-3}{\sqrt x(\sqrt x-3)}\\=\frac{2x-3-\sqrt x+3}{\sqrt x(\sqrt x-3)} =\frac{2x-\sqrt x}{\sqrt x(\sqrt x-3)}=\frac{\sqrt x(2\sqrt x-1)}{\sqrt x(\sqrt x-3)}\\=\frac{2\sqrt x-1}{\sqrt x-3}(đpcm)\)

Câu 2:

Ta có: 

\(A-B<0\Leftrightarrow \frac{x}{\sqrt x-3}-\frac{2\sqrt x-1}{\sqrt x-3}<0\\\Leftrightarrow \frac{x-2\sqrt x+1}{\sqrt x-3}<0\\\Leftrightarrow \frac{ (\sqrt x-1)^2}{\sqrt x-3}<0\\ \Leftrightarrow \begin{cases} \sqrt x-1\ne0\\ \sqrt x-3<0 \end{cases} (\text{vì }(\sqrt x-1)^2\ge 0)\\ \Leftrightarrow \begin{cases} \sqrt x\ne 1\\ \sqrt x<3 \end{cases}\Leftrightarrow \begin{cases} x\ne 1\\ 0\le x<9 \end{cases} \)

Kết hợp với ĐKXĐ của x, ta được: \(0< x<9;x\ne 1\)

$Toru$

Mik nghe nói chỉ quản lí mới duyệt được hình ảnh

Olm chào em, những câu hỏi hoặc câu trả lời có chứa ảnh phải đươc quản trị viên như cô duyệt mới có thể hiển thị trên Olm em nhé. 

Cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức cuộc sống.

ĐKXĐ: \(x>0;x\ne 4\)

\(\frac{\sqrt x-1}{\sqrt x-2}-\frac{5\sqrt x-8}{x-2\sqrt x}=\frac{\sqrt x(\sqrt x-1)}{\sqrt x(\sqrt x-2)}-\frac{5\sqrt x-8}{\sqrt x(\sqrt x-2)}\\= \frac{x-\sqrt x-(5\sqrt x+8)}{\sqrt x(\sqrt x-2)}=\frac{x-6\sqrt x+8}{\sqrt x(\sqrt x-2)}\\=\frac{(\sqrt x-2)(\sqrt x-4)}{\sqrt x(\sqrt x-2)}=\frac{\sqrt x-4}{\sqrt x}\)

Hết số thời gian là :

1 giờ 30 phút x 5 = 5 giờ 150 phút = 7 giờ 30 phút

Đ/s:...

                 Giải:

Người đó làm 5 sản phẩm như thế hết thời gian là:

              1 giờ 30 phút x 5 = 5 giờ 150 phút

              5 giờ 150 phút = 7 giờ 30 phút 

Kết luận người đó làm 5 sản phẩm như thế hết 7 giờ 30 phút

1: Xét ΔDIN vuông tại I và ΔDKP vuông tại K có

\(\widehat{IDN}=\widehat{KDP}\)(hai góc đối đỉnh)

Do đó: ΔDIN~ΔDKP

2: Xét ΔMIN vuông tại I và ΔMKP vuông tại K có

\(\widehat{IMN}=\widehat{KMP}\)

Do đó: ΔMIN~ΔMKP

=>\(\dfrac{MI}{MK}=\dfrac{MN}{MP}\)

=>\(MI\cdot MP=MN\cdot MK\)

- Theo em, y và x liên hệ với nhau theo biểu thức: \(y=\frac{14,4}{x}\)

- Nếu số bánh gói được là x = 18 thì khối lượng mỗi bánh là:  \(y=\frac{14,4}{18}=0,8\mathit{(kg)}\)