Giúp tớ giải bài này tớ cần gấp 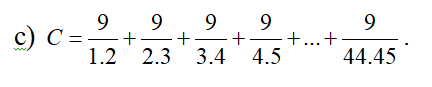
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(11\in N;11\in Q;11\in Z\)
b: \(-26\in Q;-26\in Z\)
c: \(\dfrac{1}{5}\in Q\)
d: \(-\dfrac{3}{4}\in Q\)

2h30p=2,5 giờ
Vận tốc lúc đi của cano là \(\dfrac{60}{2,5}=24\)(km/h)
vận tốc lúc về của cano là \(\dfrac{60}{3}=20\)(km/h)
Gọi vận tốc thật của cano là x(km/h)
(Điều kiện: x>0)
Vận tốc của dòng nước là 24-x(km/h)
Vận tốc lúc về là 20km/h nên ta có:
x-(24-x)=20
=>x-24+x=20
=>2x=20+24=44
=>\(x=\dfrac{44}{2}=22\left(nhận\right)\)
Vậy: Vận tốc thật của cano là 22km/h
Vận tốc của dòng nước là 24-22=2km/h

Gọi số tiền bác Nam đầu tư vào khoản trái phiếu là x(triệu đồng)
(Điều kiện: x>0)
Số tiền bác Nam đầu tư vào khoản gửi tiết kiệm là:
900-x(triệu đồng)
Số tiền lãi bác Nam thu được khi đầu tư vào khoản trái phiếu là:
\(x\cdot7\%=0,07x\)(triệu đồng)
Số tiền lãi bác Nam thu được khi gửi tiết kiệm là:
\(\left(900-x\right)\cdot6\%=0,06\left(900-x\right)\)(triệu đồng)
Tổng số tiền lãi thu được là 58 triệu đồng nên ta có:
0,07x+0,06(900-x)=58
=>0,07x+54-0,06x=58
=>0,01x=4
=>x=400(nhận)
Vậy: số tiền bác Nam đầu tư vào khoản trái phiếu là 400(triệu đồng)
Số tiền bác Nam đầu tư vào khoản gửi tiết kiệm là:900-400=500(triệu đồng)

Tổng vận tốc hai xe là 270:3=90(km/h)
Gọi vận tốc xe thứ nhất là x(km/h)
(Điều kiện: 0<x<90)
Vận tốc xe thứ hai là 90-x(km/h)
Độ dài quãng đường xe thứ nhất đi được sau 3 giờ là:
3x(km)
Độ dài quãng đường xe thứ hai đi được sau 3 giờ là:
3(90-x)(km)
Xe thứ nhất đi được nhiều hơn xe thứ hai 6km nên ta có:
3x-3(90-x)=6
=>3x-270+3x=6
=>6x=276
=>x=276/6=46(nhận)
Vậy: Vận tốc xe thứ nhất là 46km/h
Vận tốc xe thứ hai là 90-46=44km/h

Ta có: QE\(\perp\)OM
NP\(\perp\)OM
Do đó: QE//NP
Ta có: PQ\(\perp\)Ox
MN\(\perp\)Ox
Do đó: PQ//MN

Gọi số linh kiện tổ A và tổ B lắp được trong 1 ngày lần lượt là x(linh kiện) và y(linh kiện)
(Điều kiện: \(x,y\in Z^+\))
Mỗi ngày tổ A lắp ráp được nhiều hơn tổ B là 30 linh kiện nên x-y=30(1)
Số linh kiện tổ A lắp được trong 6 ngày là 6x(linh kiện)
Số linh kiện tổ B lắp được trong 5 ngày là 5y(linh kiện)
Nếu tổ A lắp trong 6 ngày và tổ B lắp trong 5 ngày thì hai tổ lắp được 2600 bộ nên 6x+5y=2600(2)
Từ (1),(2) ta có hệ:
\(\left\{{}\begin{matrix}x-y=30\\6x+5y=2600\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-6y=180\\6x+5y=2600\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+5y-6x+6y=2600-180\\x-y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11y=2420\\x=y+30\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=220\\x=220+30=250\end{matrix}\right.\left(nhận\right)\)
Vậy: số linh kiện tổ A và tổ B lắp được trong 1 ngày lần lượt là 250(linh kiện) và 220(linh kiện)

Gọi năng suất dự định của công nhân đó là x(sản phẩm/giờ)
(Điều kiện: \(x\in Z^+\))
Năng suất thực tế là x+2(sản phẩm/giờ)
Thời gian dự kiến hoàn thành là \(\dfrac{15}{x}\left(giờ\right)\)
Thời gian thực tế hoàn thành là \(\dfrac{25}{x+2}\left(giờ\right)\)
Vì người đó hoàn thành đúng thời hạn nên ta có:
\(\dfrac{15}{x}=\dfrac{25}{x+2}\)
=>25x=15(x+2)
=>10x=30
=>x=3(nhận)
vậy: Năng suất dự định là 3 sản phẩm/giờ

Gọi vận tốc lúc đi là x(km/h)
(Điều kiện: x>0)
Vận tốc lúc về là x+10(km/h)
Thời gian đi là \(\dfrac{150}{x}\left(giờ\right)\)
Thời gian về là \(\dfrac{150}{x+10}\left(giờ\right)\)
Tổng thời gian cả đi lẫn về là 5h30p=5,5 giờ nên ta có:
\(\dfrac{150}{x}+\dfrac{150}{x+10}=5,5\)
=>\(\dfrac{1}{x}+\dfrac{1}{x+10}=\dfrac{150}{5,5}=\dfrac{300}{11}\)
=>\(\dfrac{x+10+x}{x\left(x+10\right)}=\dfrac{300}{11}\)
=>300x(x+10)=11(2x+10)
=>\(300x^2+3000x-22x-110=0\)
=>\(300x^2+2978x-110=0\)(1)
\(\text{Δ}=2978^2-4\cdot300\cdot\left(-110\right)=9000484>0\)
Do đó: Phương trình (1) có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-2978-\sqrt{9000484}}{600}\left(loại\right)\\x=\dfrac{-2978+\sqrt{9000484}}{600}\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đi là \(\dfrac{-2978+\sqrt{9000484}}{600}\left(\dfrac{km}{h}\right)\)

Độ dài cạnh phần đất còn lại là 16-x(m)
Diện tích phần đất còn lại là 196m2 nên ta có:
\(\left(16-x\right)^2=196\)
=>\(\left(x-16\right)^2=196\)
=>\(\left[{}\begin{matrix}x-16=14\\x-16=-14\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Vậy: Độ dài bề rộng là 2m









\(C=\dfrac{9}{1\cdot2}+\dfrac{9}{2\cdot3}+...+\dfrac{9}{44\cdot45}\)
\(=9\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{44\cdot45}\right)\)
\(=9\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{44}-\dfrac{1}{45}\right)\)
\(=9\left(1-\dfrac{1}{45}\right)=9\cdot\dfrac{44}{45}=\dfrac{44}{5}\)