Con người có bao nhiêu bộ phận cơ thể?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

My favorite hobby is playing badminton. I started about 2 years ago. I play badminton with my father everyday afternoon. I always play badminton at home. I think it is a sport very good for our health.
My favorite hobby is playing football. I started playing in the summer 2 years ago. I play football with my friends every afternoon. We always play football at home. I think it is a very good sport for our health.


C = \(x^2\) - 12 \(x\) + 34
C = (\(x^2\) - 12\(x\) + 36) - 2
C = (\(x\) - 6)2 - 2
Vì (\(x\) - 6)2 ≥ 0 ⇒ ( \(x\) - 6)2 - 2 ≥ -2
C(min) = - 2 ⇔ \(x\) - 6 = 0 ⇔ \(x\) = 6
Vậy giá trị nhỏ nhất của biểu thức là - 2 xảy ra khi \(x\) = 6
C = �2x2 - 12 �x + 34
C = (�2x2 - 12�x + 36) - 2
C = (�x - 6)2 - 2
Vì (�x - 6)2 ≥ 0 ⇒ ( �x - 6)2 - 2 ≥ -2
C(min) = - 2 ⇔ �x - 6 = 0 ⇔ �x = 6
Vậy giá trị nhỏ nhất của biểu thức là - 2 diễn ra khi �x = 6

A = - 4\(x\)2 + 5\(x\) - 3
A = -( 4\(x^2\) - 5\(x\) + \(\dfrac{25}{16}\)) - \(\dfrac{23}{16}\)
A = -( 2\(x\) - \(\dfrac{5}{4}\))2 - \(\dfrac{23}{16}\)
Vì ( 2\(x\) - \(\dfrac{5}{4}\))2 ≥ 0; ⇒ - ( 2\(x\) - \(\dfrac{5}{4}\))2 ≤ 0 ⇒ -( 2 \(x\) - \(\dfrac{5}{4}\))2 - \(\dfrac{23}{16}\) ≤ - \(\dfrac{23}{16}\)
A(max) = - \(\dfrac{23}{16}\) ⇔ 2\(x\) - \(\dfrac{5}{4}\) = 0 ⇔ \(x\) = \(\dfrac{5}{4}\): 2 = \(\dfrac{5}{8}\)
Kết luận giá trị lớn nhất của biểu thức là - \(\dfrac{23}{16}\) xáy ra khi \(x\) = \(\dfrac{5}{8}\)

Lời giải:
Đặt $x-y=a; y-z=b, z-x=c$
$\Rightarrow a+b+c=0$
Theo đề ta có:
$(x-y)^2+(y-z)^2+(z-x)^2=[(z-x)-(x-y)]^2+[(x-y)-(y-z)]^2+[(y-z)-(z-x)]^2$
$\Leftrightarrow a^2+b^2+c^2=(c-a)^2+(a-b)^2+(b-c)^2$
$\Leftrightarrow a^2+b^2+c^2=2a^2+2b^2+2c^2-2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=a^2+b^2+c^2+2(ab+bc+ac)$
$\Leftrightarrow 2(a^2+b^2+c^2)=(a+b+c)^2=0$
$\Rightarrow a^2+b^2+c^2=0$
$\Rightarrow a=b=c=0$
$\Leftrightarrow x-y=y-z=z-x=0$
$\Leftrightarrow x=y=z$

`A = -25x^2 +30x -2 = -(25x^2 -30x +2)`
`= -[(5x)^2 - 2*5x*3 +3^2 +2-3^2]`
`=-[(5x-3)^2 -7] = 7-(5x-3)^2`
Do `-(5x-3)^2 <= 0 AA x`
`=> 7- (5x-3)^2 <0 AA x `
hay `A<0 AA x (đpcm)`
từ đã có gì đó hơi sai sai
\(7-\left(5x-3\right)^2=-\left(5x-3\right)^2+7\) mà=)))
sao nó lại nhỏ hơn không nhỉ=)))

`B =9x^2 +6x = (3x)^2 + 2*3x*1 +1 -1)`
`=(3x +1)^2 -1`
Do `(3x+1)^2 >=0 AA x`
`=> (3x+1)^2 -1 >=-1 AA x`
hay `B>=-1`
Dấu ''='' xảy ra khi và chỉ khi `3x+1=0 =>x =-1/3`
Vậy GTNN của `B=-1` khi `x=-1/3`
B = 9\(x^2\) + 6\(x\)
B = 9\(x^2\) + 6\(x\) + 1 - 1
B = (3\(x\) + 1)2 - 1
Vì (3\(x\) + 1)2 ≥ 0 ⇒ (3\(x\) + 1)2 - 1 ≥ -1
B(min) = -1⇔ \(x\) = - \(\dfrac{1}{3}\)
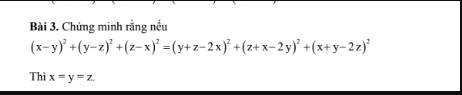
RRất nhiều em nha: Đầu, cổ, chân , tay, mũi , mắt, lưng, ngực,...