
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TH1: x<1
Phương trình sẽ trở thành:
\(1-x+2-x+3-x=-4x\)
=>-4x=-3x+6
=>-x=6
=>x=-6(nhận)
TH2: 1<=x<2
Phương trình sẽ trở thành:
\(x-1+2-x+3-x=-4x\)
=>-4x=-x+4
=>-3x=4
=>\(x=-\dfrac{4}{3}\left(loại\right)\)
TH3: 2<=x<3
Phương trình sẽ trở thành:
\(x-1+x-2+3-x=-4x\)
=>x=-4x
=>x=0(loại)
TH4: x>=3
Phương trình sẽ trở thành:
x-1+x-2+x-3=-4x
=>-4x=3x-6
=>-7x=-6
=>\(x=\dfrac{6}{7}\left(loại\right)\)

\(\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}=1,2\\\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=1,2-8\dfrac{1}{5}\\ \Rightarrow \left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=-7\)
Nhận xét:
\(\left\{{}\begin{matrix}\left|2\dfrac{1}{5}-x\right|\ge0,\forall x\\\left|x-\dfrac{1}{5}\right|\ge0,\forall x\end{matrix}\right.\\
\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|\ge0,\forall x\)
Mà \(-7< 0\) nên:
Không tìm được giá trị \(x\) thỏa mãn đề bài
Vậy...

\(5\cdot\dfrac{5^{37}-1}{5^{38}-1}=\dfrac{5^{38}-5}{5^{38}-1}=1-\dfrac{4}{5^{38}-1}\)
\(\dfrac{5\left(5^{36}+1\right)}{5^{37}+1}=\dfrac{5^{37}+5}{5^{37}+1}=1+\dfrac{4}{5^{37}+1}\)
mà \(-\dfrac{4}{5^{38}-1}< \dfrac{4}{5^{37}+1}\)
nên \(5\cdot\dfrac{5^{37}-1}{5^{38}-1}< 5\cdot\dfrac{5^{36}+1}{5^{37}+1}\)
=>\(\dfrac{5^{37}-1}{5^{38}-1}< \dfrac{5^{36}+1}{5^{37}+1}\)

\(x^2+3x+1⋮x+1\)
=>\(x^2+x+2x+2-1⋮x+1\)
=>\(-1⋮x+1\)
=>\(x+1\in\left\{1;-1\right\}\)
=>\(x\in\left\{0;-2\right\}\)

\(\left|x-2\right|>=0\forall x\)
\(\left|2x+y-z\right|>=0\forall x,y,z\)
\(\left|2z+1\right|>=0\forall z\)
Do đó: \(\left|x-2\right|+\left|2x+y-z\right|+\left|2z+1\right|>=0\forall x,y,z\)
mà \(\left|x-2\right|+\left|2x+y-z\right|+\left|2z+1\right|< =0\)
nên Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\2x+y-z=0\\2z+1=0\\\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\z=-\dfrac{1}{2}\\y=-2x+z=-2\cdot2+\dfrac{-1}{2}=-4-\dfrac{1}{2}=-\dfrac{9}{2}\end{matrix}\right.\)

\(2^2+3^2+...+2021^2\)
\(=\left(1^2+2^2+...+2021^2\right)-1\)
\(=\dfrac{2021\cdot\left(2021+1\right)\left(2\cdot2021+1\right)}{6}=1\)
\(=2753594310\)

Gọi số điểm cho trước là x(điểm)
(Điều kiện: \(x\in Z^+;x>3\))
Số điểm không thẳng hàng là x-3(điểm)
TH1: vẽ 1 đường thẳng đi qua 3 điểm thẳng hàng
=>Có 1 đường thẳng
TH2: Chọn 2 điểm bất kì trong x-3 điểm còn lại
Số đường thẳng là \(C^2_{x-3}=\dfrac{\left(x-3\right)!}{\left(x-3-2\right)!\cdot2!}=\dfrac{\left(x-4\right)\left(x-3\right)}{2}\)(đường)
TH3: Chọn 1 điểm trong 3 điểm thẳng hàng, 1 điểm trong x-3 điểm còn lại
=>Có 3(x-3) đường thẳng
Tổng số đường thẳng là 120 đường nên ta có:
\(1+\dfrac{\left(x-4\right)\left(x-3\right)}{2}+3\left(x-3\right)=120\)
=>\(\dfrac{2+\left(x-4\right)\left(x-3\right)+6\left(x-3\right)}{2}=120\)
=>2+(x-4)(x-3)+6(x-3)=240
=>\(2+x^2-7x+12+6x-18=240\)
=>\(x^2-x-244=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{1+\sqrt{977}}{2}\left(loại\right)\\x=\dfrac{1-\sqrt{977}}{2}\left(loại\right)\end{matrix}\right.\)

1: \(5^{x+4}-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(5^{x+3}\cdot5-3\cdot5^{x+3}=2\cdot5^{11}\)
=>\(2\cdot5^{x+3}=2\cdot5^{11}\)
=>x+3=11
=>x=8
2: \(\dfrac{1}{2}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\cdot\left(\dfrac{1}{2}+4\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=2^6\)
=>x=6
3: \(9^{2x+1}=27^3\)
=>\(3^{4x+2}=3^9\)
=>4x+2=9
=>4x=7
=>\(x=\dfrac{7}{4}\)
4: \(2^{-1}\cdot2^x+4\cdot2^x=9\cdot2^5\)
=>\(2^x\left(4+\dfrac{1}{2}\right)=9\cdot2^5\)
=>\(2^x\cdot\dfrac{9}{2}=9\cdot2^5\)
=>\(2^x=9\cdot2^5:\dfrac{9}{2}=2^6\)
=>x=6
5: \(\left(2x-1\right)^3=\dfrac{8}{27}\)
=>\(\left(2x-1\right)^3=\left(\dfrac{2}{3}\right)^3\)
=>\(2x-1=\dfrac{2}{3}\)
=>\(2x=\dfrac{2}{3}+1=\dfrac{5}{3}\)
=>\(x=\dfrac{5}{3}:2=\dfrac{5}{6}\)

b: \(\dfrac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}\cdot\dfrac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=8^x\)
=>\(8^x=\dfrac{4\cdot4^5}{3\cdot3^5}\cdot\dfrac{6\cdot6^5}{2\cdot2^5}\)
=>\(8^x=\dfrac{4^6}{2^6}\cdot\dfrac{6^6}{3^6}=2^6\cdot2^6=2^{12}=\left(2^3\right)^4=8^4\)
=>x=4
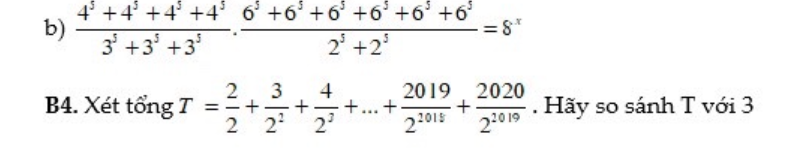
a: Oy nằm giữa Ox và Ot
=>\(\widehat{xOy}+\widehat{yOt}=\widehat{xOt}\)
=>\(\widehat{yOt}+30^0=50^0\)
=>\(\widehat{yOt}=20^0\)
b: Vì Ox là tia đối của tia Oz nên \(\widehat{xOz}=180^0\)