
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Gọi tuổi anh và tuổi em hiện nay là $3a$ và $a$ (tuổi)
6 năm nữa tuổi anh là: $3a+6$
6 năm nữa tuổi em là: $a+6$
Theo bài ra ta có: $3a+6=2(a+6)$
$\Rightarrow a=6$ (tuổi)
Vậy tuổi em hiện nay là 6 tuổi. Tuổi anh hiện nay là $6.3=18$ tuổi.

Số sách ở thư viện thứ nhất:
\(\left(15000+3000\right):2=9000\) (cuốn sách)
Số sách ở thư viện thứ hai:
\(15000-9000=6000\) (cuốn sách)
Đáp số:....

2\(xy\) + 6\(x\) - \(y\) = 6
2\(xy\) + 6\(x\) = 6 + \(y\)
\(x\)(2\(y\) + 6) = 6 + \(y\)
\(x\) = (6 + \(y\) ): (2\(y\)+6)
\(x\) \(\in\) Z ⇔ 6 + \(y\) ⋮ 2\(y\) + 6 ⇒ 2.(6+\(y\)) ⋮ 2\(y\) + 6 ⇒ 12 + 2\(y\) ⋮ 2\(y\) + 6
⇒ 2\(y\) + 6 + 6 ⋮ 2\(y\) + 6 ⇒ 6 ⋮ 2\(y\) + 6 ⇒ 3 ⋮ y + 3
Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
| \(y+3\) | -3 | -1 | 1 | 3 |
| \(y\) | -6 | -4 | -2 | 0 |
| \(x\) = (6+\(y\)):(2\(y\)+6) | 0 | -1 | 2 | 1 |
Các cặp (\(x;y\)) thỏa mãn đề bài lần lượt là:
(\(x\); \(y\)) = (0; -6); (-1; -4); (2; -2) ; (1; 0)

Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
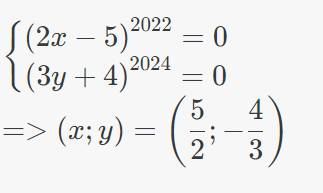 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)

\(\left[\left(0,1\right)^2\right]^0+\left[\left(\dfrac{1}{7}\right)^{-1}\right]^2\cdot\dfrac{1}{49}\cdot\left[\left(2^2\right)^3:2^5\right]\)
\(=1+7^2\cdot\dfrac{1}{49}\cdot\left(2^6:2^5\right)\)
\(=1+49\cdot\dfrac{1}{49}\cdot2\)
\(=1+1\cdot2\)
\(=3\)

`(4*2^5) \div (2^3*1/6)`
`= (2^2*2^5) \div (8/6)`
`= 2^7 \div 4/3`
`= 96`

\(\left(0,125\right)^3.512=\left(0,125\right)^3.8^3=\left(0,125.8\right)^3=1^3=1\)
\(\left(0,125\right)^3.512\)
\(=\left(0,125\right)^3.8^3\)
\(=\left(0,125\cdot8\right)^3\)
\(=1^3\)
\(=1\)
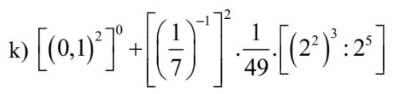
Mình làm mẫu 1 câu thôi nhé !
Bài 1:
a) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{4}=\dfrac{x-y}{7-4}=\dfrac{30}{3}=10\)
\(\Rightarrow\dfrac{x}{7}=10\Rightarrow x=70\)
\(\Rightarrow\dfrac{y}{4}=10\Rightarrow y=40\)