P554.(Mức B)cho x,y,z là các số thực dương,thoả mãn x2+y2+z2=1,chứng minh rằng:\(\frac{1}{1+yz}\le\frac{\sqrt{2}}{x+y+z}.\)mình chưa biết giải.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có phải phép tính là
\(\frac{1}{2}+\frac{1}{5}x0+vôcực\)
ko bạn nếu đúng thì kết quả là vô cực


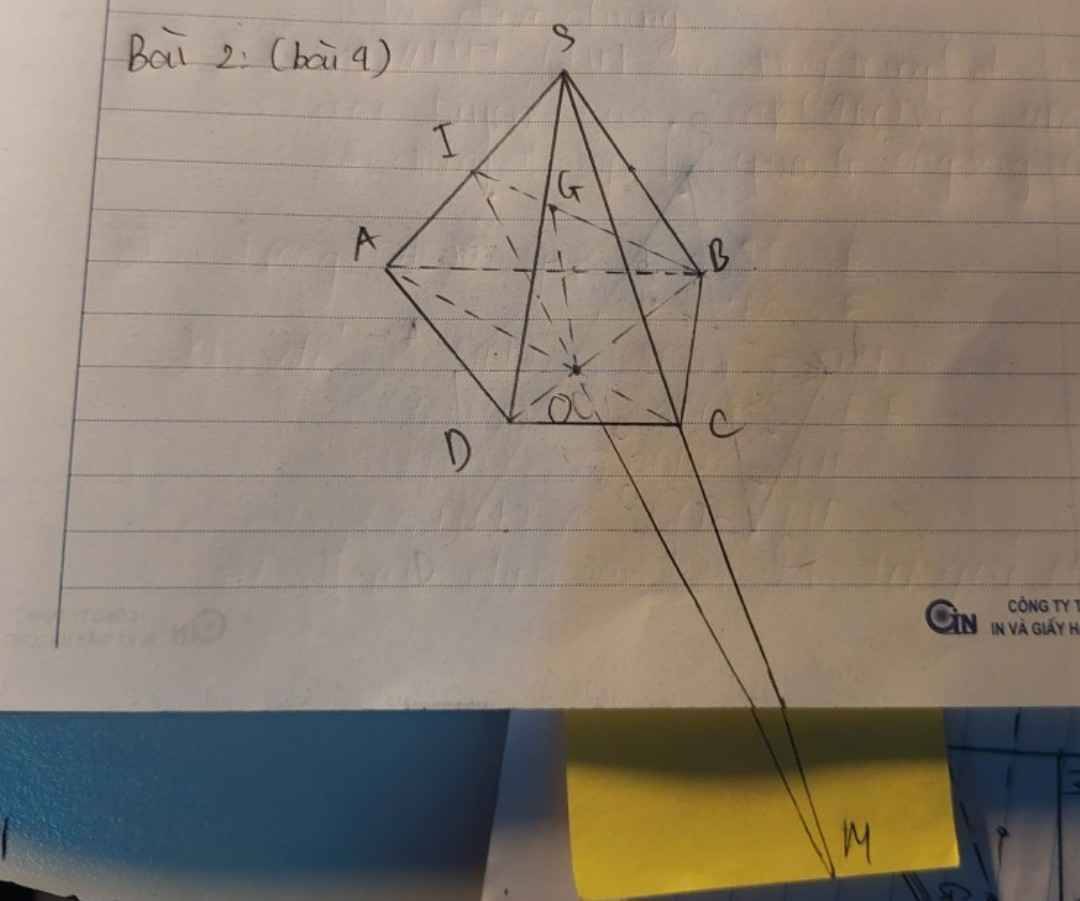
+ Ta tìm giao tuyến của mp (IBC) và (SAD)
+ Trong mặt phẳng (SAD) , gọi giao điểm của Ix và SD là J
⇒ IJ // BC.
Lại có; I là trung điểm của SA nên J là trung điểm của SD.
⇒ A và B đều đúng.
+ Giao tuyến của (IBC) và (SAD )là IJ.
Xét tam giác SAD có I và J lần lượt là trung điểm của SA và SD nên IJ là đường trung bình của tam giác
⇒ IJ // AD // BC mà BC ⊂ (SBC)
⇒ IJ // mp(SBC) nên C đúng
+ Ta tìm giao tuyến của mp (IBC) và (SAD)
+ Trong mặt phẳng (SAD) , gọi giao điểm của Ix và SD là J
⇒ IJ // BC.
Lại có; I là trung điểm của SA nên J là trung điểm của SD.
⇒ A và B đều đúng.
+ Giao tuyến của (IBC) và (SAD )là IJ.
Xét tam giác SAD có I và J lần lượt là trung điểm của SA và SD nên IJ là đường trung bình của tam giác
⇒ IJ // AD // BC mà BC ⊂ (SBC)
⇒ IJ // mp(SBC) nên C đúng


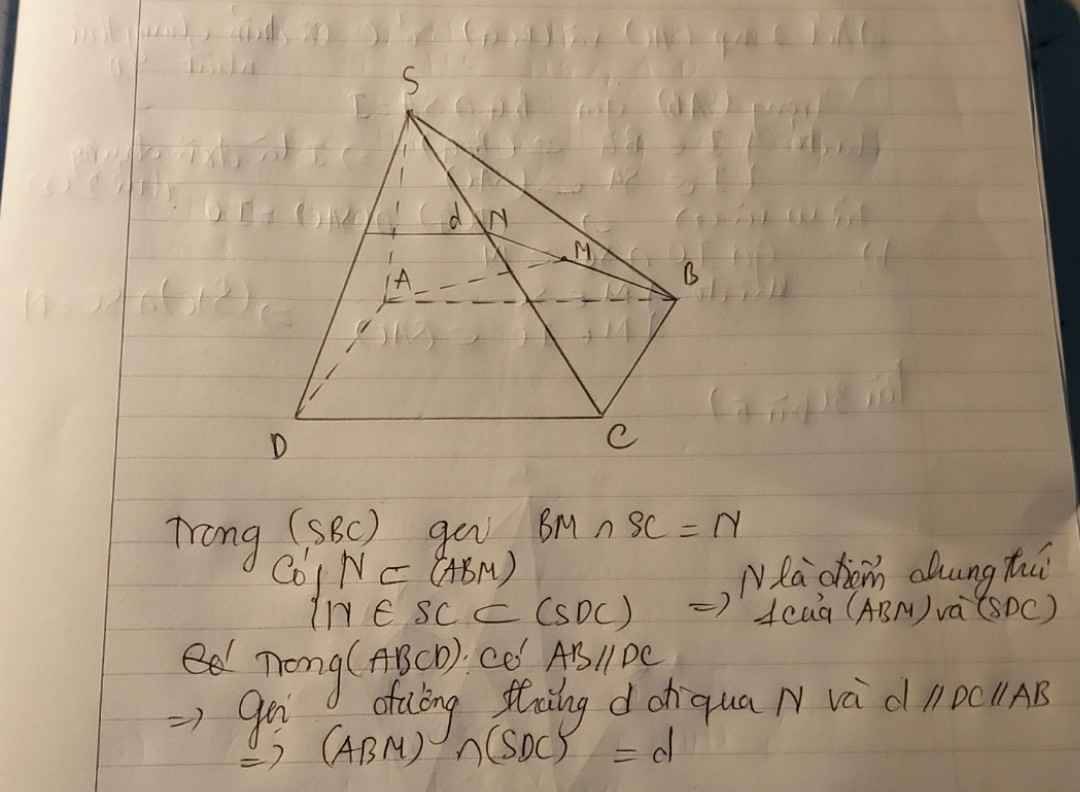
Xét ba mặt phẳng (MCD),(SAB),(ABCD)(MCD),(SAB),(ABCD) có:
⎧⎪⎨⎪⎩(MCD)∩(ABCD)=CD(MCD)∩(SAB)=MN(ABCD)∩(SAB)=AB{(MCD)∩(ABCD)=CD(MCD)∩(SAB)=MN(ABCD)∩(SAB)=AB
Mà AB//CDAB//CD nên MN//AB//CDMN//AB//CD
Vậy MN//CDMN//CD.
Đáp án B đúng, D sai.
Ngoài ra, quan sát hình vẽ ta thấy MN,SDMN,SD chéo nhau, MN,SCMN,SC chéo nhau nên các

a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có:
⇒ (SAD) ∩ (SBC) = Sx
Và Sx // AD // BC.
b) Ta có: MN // IA // CD
Mà
(G là trọng tâm của ∆SAB) nên
⇒ GN // SC
SC ⊂ (SCD) ⇒ GN // (SCD)
c) Giả sử IM cắt CD tại K ⇒ SK ⊂ (SCD)
MN // CD ⇒
Ta có:



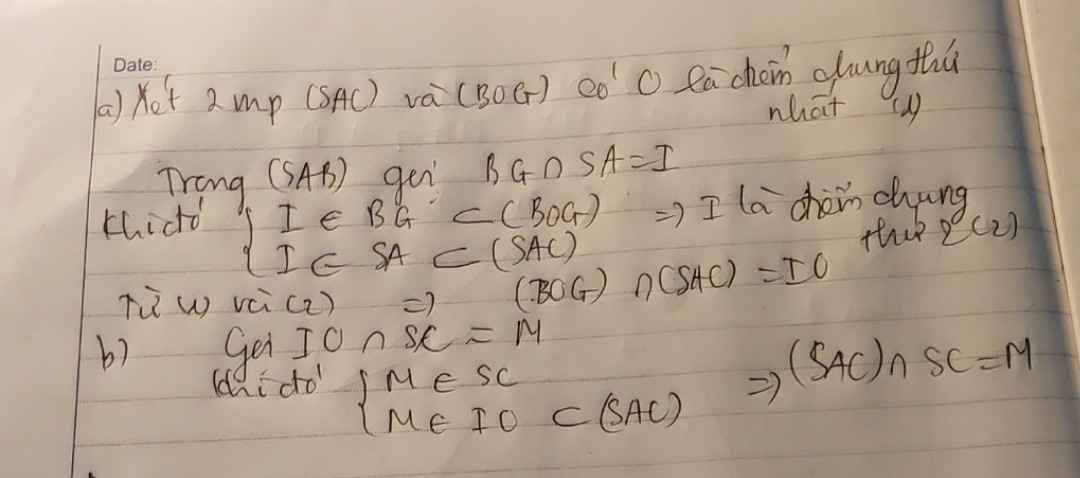

Đặt \(P=\frac{x}{\sqrt{1+x^2}}+\frac{y}{\sqrt{1+y^2}}+\frac{z}{\sqrt{1+z^2}}+\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\)
Do x,y,z là các số thực dương nên ta biến đổi \(P=\frac{1}{\sqrt{1+\frac{1}{x^2}}}+\frac{1}{\sqrt{1+\frac{1}{y^2}}}+\frac{1}{\sqrt{1+\frac{1}{z^2}}}+\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\)
Đặt \(a=\frac{1}{x^2};b=\frac{1}{y^2};c=\frac{1}{z^2}\left(a,b,c>0\right)\)thì \(xy+yz+zx=\frac{1}{\sqrt{ab}}+\frac{1}{\sqrt{bc}}+\frac{1}{\sqrt{ca}}=1\)và \(P=\frac{1}{\sqrt{1+a}}+\frac{1}{\sqrt{1+b}}+\frac{1}{\sqrt{1+c}}+a+b+c\)
Biến đổi biểu thức P=\(\left(\frac{1}{2\sqrt{a+1}}+\frac{1}{2\sqrt{a+1}}+\frac{a+1}{16}\right)+\left(\frac{1}{2\sqrt{b+1}}+\frac{1}{2\sqrt{b+1}}+\frac{b+1}{16}\right)\)\(+\left(\frac{1}{2\sqrt{c+1}}+\frac{1}{2\sqrt{c+1}}+\frac{c+1}{16}\right)+\frac{15a}{16}+\frac{15b}{16}+\frac{15c}{b}-\frac{3}{16}\)
Áp dụng Bất Đẳng Thức Cauchy ta có
\(P\ge3\sqrt[3]{\frac{a+1}{64\left(a+1\right)}}+3\sqrt[3]{\frac{b+1}{64\left(b+1\right)}}+3\sqrt[3]{\frac{c+1}{64\left(c+1\right)}}+\frac{15a}{16}+\frac{15b}{16}+\frac{15c}{16}-\frac{3}{16}\)
\(=\frac{33}{16}+\frac{15}{16}\left(a+b+c\right)\ge\frac{33}{16}+\frac{15}{16}\cdot3\sqrt[3]{abc}\)
Mặt khác ta có \(1=\frac{1}{\sqrt{ab}}+\frac{1}{\sqrt{bc}}+\frac{1}{\sqrt{ca}}\ge3\sqrt[3]{\frac{1}{abc}}\Leftrightarrow abc\ge27\)
\(\Rightarrow P\ge\frac{33}{16}+\frac{15}{16}\cdot3\sqrt[3]{27}=\frac{33}{16}+\frac{15}{16}\cdot9=\frac{21}{2}\)
Dấu "=" xảy ra khi a=b=c hay \(x=y=z=\frac{\sqrt{3}}{3}\)
Ai giải đc cho 5 k và được kết bạn.(thực ra mình lớp 4,đọc tạp chí pi bố mik cũng không hiểu gì luôn.)