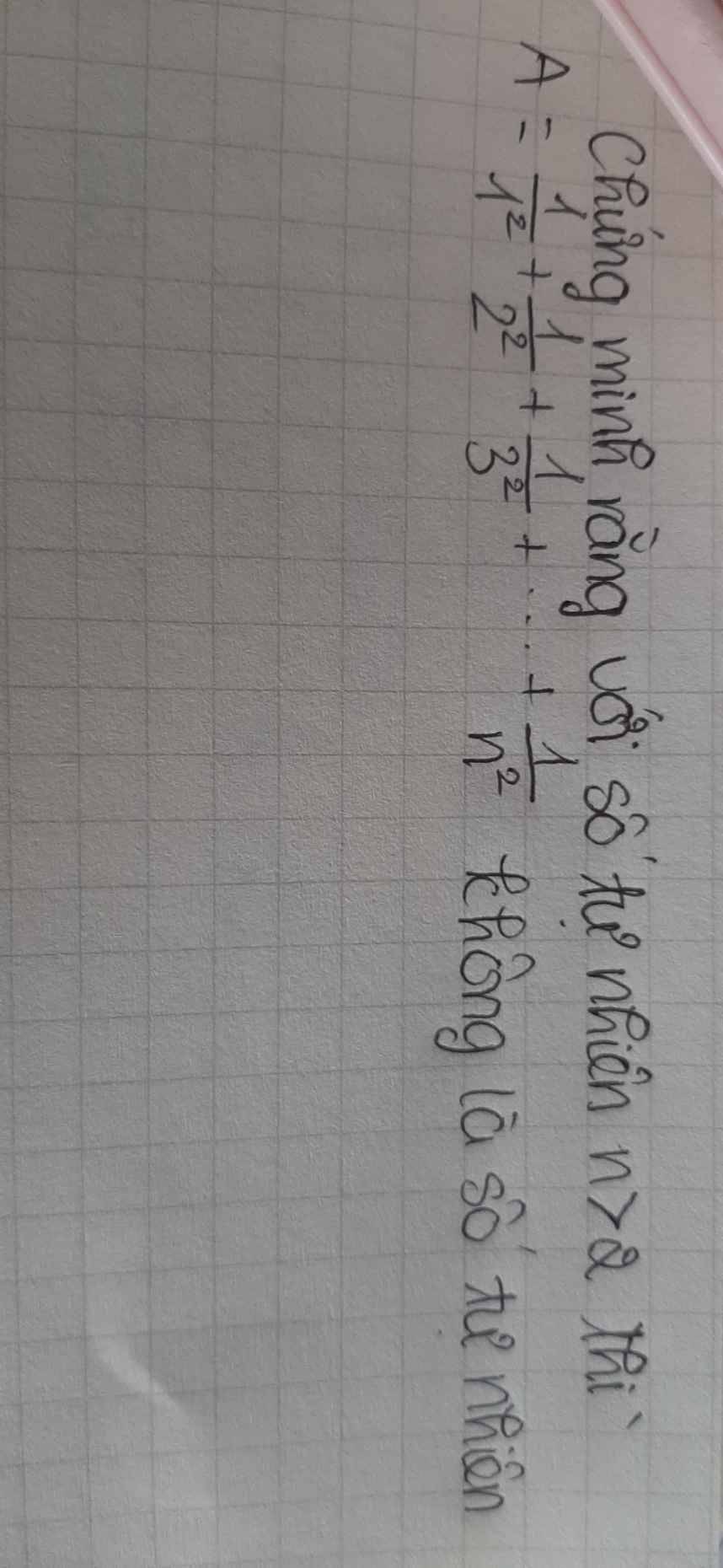\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)

...

\(\dfrac{1}{n^2}< \dfrac{1}{n-1}-\dfrac{1}{n}\)

Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}=1-\dfrac{1}{n}\)

=>\(A=\dfrac{1}{1^2}+\dfrac{1}{2^2}+...+\dfrac{1}{n^2}< 2-\dfrac{1}{n}< 2\)

=>A<2

mà A>1

nên 1<A<2

=>A không là số tự nhiên

ta có 

1/2^2 =1/2.2 < 1/1.2    (do 1/2.2 = 1/4 <1/2)

1/3^2 = 1/3.3 <1/2.3

1/4^2= 1/4. 4 <1/3.4

......                                 (làm tương tự thế)

1/n^2 =1/n.n < 1/(n-1).n

suy ra 1/2^2 + 1/3^2 + 1/4^2 +....+1/n^2 < 1/1.2 + 1/2.3 + 1/3.4 +...+1/n.(n+1)

ta có 1/1.2 + 1/2.3 + 1/3.4 + ... +1/(n-1).n

       =1/1 - 1/2 + 1/2 - 1/3  + 1/3 - 1/4 + .... +1/n-1 -1/n

       =1/1 - 1/n                                       (1/n-1)triệt tiêu phía trước)

suy ra 1/2^2 + 1/3^2 + 1/4^2 + ...+1/n^2 < 1-1/n <1

mà 1/2^2 + 1/3^2 + ...+1/n^2 >0

suy ra 0<1/2^2 +1/3^2+...+1/n^2<1

suy ra 1/2^2 +1/3^2 +....+1/n^2 ko là số tự nhiên với số tự nhiên n>2

bạn đừng ghi cái ngoặc nhé

104

a) 60,7 + 25,5 - 38,7

= (60,7 - 38,7) + 25,5

= 22 + 25,5

= 47,5

Câu b) bạn xem lại dấu đi nhé.

0<0,7<1,2

0>-2,3>-2,33

Do đó: -2,33<-2,3<0<0,7<1,2

Sắp xếp tăng dần:

-2,33 < -2,3 < 0 < 0,7 < 1,2

Làm tròn đến hàng phần mười;

\(-482,7936\simeq-482,8\)

\(-578,7283\simeq-578,7\)

Làm tròn đến hàng phần trăm:

\(-482,7936\simeq-482,79\)

\(-578,7283\simeq-578,73\)

Làm tròn đến hàng phần nghìn:

\(-482,7936\simeq-482,794\)

\(-578,7283\simeq-578,728\)

a: Số học sinh trung bình là \(40\cdot40\%=16\left(bạn\right)\)

Số học sinh khá là \(16\cdot\dfrac{7}{8}=14\left(bạn\right)\)

Số học sinh giỏi là 40-16-14=10(bạn)

b: Tỉ số phần trăm giữa số học sinh giỏi so với cả lớp là:

\(\dfrac{10}{40}=\dfrac{1}{4}=25\%\)

a) Số học sinh trung bình:

\(40.40\%=16\) (học sinh)

Số học sinh khá:

\(16.\dfrac{7}{8}=14\) (học sinh)

Số học sinh giỏi:

\(40-16-14=10\) (học sinh)

b) Tỉ số phần trăm của số học sinh giỏi so với số học sinh cả lớp:

\(10.100\%:40=25\%\)