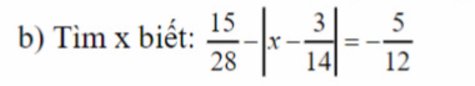
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(2x-1\right)^3=\dfrac{8}{27}\)
\(\Rightarrow\left(2x-1\right)^3=\left(\dfrac{2}{3}\right)^3\)
\(\Rightarrow2x-1=\dfrac{2}{3}\)
\(\Rightarrow2x=\dfrac{2}{3}+1\)
\(\Rightarrow2x=\dfrac{5}{3}\)
\(\Rightarrow x=\dfrac{5}{3}:2=\dfrac{5}{6}\)

\(\left(x+5\right)^3=\dfrac{-64}{125}\)
\(\Rightarrow\left(x+5\right)^3=\left(\dfrac{-4}{5}\right)^3\)
\(\Rightarrow x+5=-\dfrac{4}{5}\)
\(\Rightarrow x=-\dfrac{4}{5}-5\)
\(\Rightarrow x=-\dfrac{29}{5}\)

`@` `\text {Ans}`
`\downarrow`
`(x-1)^3 = 1/8`
`=>`\(\left(x-1\right)^3=\left(\dfrac{1}{2}\right)^3\)
`=>`\(x-1=\dfrac{1}{2}\)
`=>`\(x=\dfrac{1}{2}-1\)
`=>`\(x=-\dfrac{1}{2}\)
Vậy, `x=-1/2`


`@` `\text {Ans}`
`\downarrow`
`(-x^4 - x^3) + (x^4 + 2x^3 + 5x^2 + 3x) + (-5x^2 - 3x - x^3)`
`= -x^4 - x^3 + x^4 + 2x^3 + 5x^2 + 3x - 5x^2 - 3x - x^3`
`= (-x^4+x^4) + (-x^3 + 2x^3 - x^3) + (5x^2 - 5x^2) + (3x - 3x)`
`= 0 + 0 + 0 + 0`
`= 0`
Vậy, giá trị của biểu thức trên không phụ thuộc vào giá trị của biến.
`@` `\text {Kaizuu lv uuu}`

Ta có:
\(735=3\cdot5\cdot7^2\)
\(441=3^2\cdot7^2\)
\(294=2\cdot3\cdot7^2\)
\(\RightarrowƯCLN=\left(735,441,294\right)=3\cdot7^2=147\)

Lời giải:
Điều kiện: $x\neq 0$
Với $x\neq 0$ thì khi $x\vdots 6\Rightarrow |x|\geq |6|$
Hay $|x|\geq 6(1)$
$6\vdots x\Rightarrow |6|\geq |x|$ hay $6\geq |x|(2)$
Từ $(1); (2)\Rightarrow |x|=6\Leftrightarrow x=\pm 6$

Ta có: `gcd(450;60)=30` nên độ dài viên gạch lớn nhất có thể là `30cm`

- Mười nghìn và một triệu: KHÔNG LÀ HAI SỐ NGUYÊN TỐ CÙNG NHAU. Vì nó cùng chia hết cho 2.
- Hai số tự nhiên liên tiếp: LÀ HAI SỐ NGUYÊN TỐ CÙNG NHAU.
Gọi `d=(2a-1,2a+1)(d,a\inNN^(**);\text(d lẻ ))=>(2a+1)-(2a-1)\vdots d=>2\vdots d =>d\in{1;2}=>d=1`( do `d` lẻ `)`
- `2n+3` và `3n+4` với `n\in N^(**):` LÀ HAI SỐ NGUYÊN TỐ CÙNG NHAU.
Gọi `d=(2n+3;3n+4)=d(d\inNN^(**); \text(d lẻ))=>3(2n+3)-2(3n+4)\vdots d <=>1\vdots d =>d=1`

`@` `\text {Ans}`
`\downarrow`
`b)`
`15/28 - |x-3/14| = -5/12`
`=> |x-3/14| = 15/28 - (-5/12)`
`=> |x-3/14| = 15/28 + 5/12`
`=> |x-3/14| =20/21`
`=>`\(\left[{}\begin{matrix}x-\dfrac{3}{14}=\dfrac{20}{21}\\x-\dfrac{3}{14}=-\dfrac{20}{21}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{20}{21}+\dfrac{3}{14}\\x=-\dfrac{20}{21}+\dfrac{3}{14}\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=\dfrac{7}{6}\\x=-\dfrac{31}{42}\end{matrix}\right.\)
Vậy, `x \in {7/6; -31/42}`