Số học sinh tham quan của 1 trường khoảng từ 1200 đến 1500 em. Nếu thuê xe 30 chỗ thì thừa 21 ghế, nếu thuê xe 35 chỗ thì thừa 26 ghế, nếu thuê xe 45 chỗ thì thiếu 9 ghế. Hỏi có tất cả bao nhiêu học sinh đi tham quan?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
1
KV
5 tháng 1
(9x + 5y) ⋮ 17
⇒ 4(9x + 5y) ⋮ 17
⇒(36x + 20y) ⋮ 17
⇒ (36x + 20y - 34x - 17y) ⋮ 17
⇒ (2x + 3y) ⋮ 17
DT
Dang Tung
CTVHS
4 tháng 1
10-3n chia hết cho n-2
=> -3(n-2)+4 chia hết cho n-2
=> 4 chia hết cho n-2
=> n-2 thuộc Ư(4)={±1;±2;±4}
=> n thuộc {3;1;4;0;6;-2}
4 tháng 1
10-3n chia hết cho n-2
=> -3(n-2)+4 chia hết cho n-2
=> 4 chia hết cho n-2
=> n-2 thuộc Ư(4)={±1;±2;±4}
=> n thuộc {3;1;4;0;6;-2}
4 tháng 1
40 + ( 139 - 172 + 99 ) - ( 139 + 199 - 127 )
= 40 + 139 + 172 + 99 - 139 - 199 +127
= ( 139 - 139 ) + ( 99 - 199 ) + ( 127 - 172 + 40 )
= 0 -100 - 5
= -105
VN
Võ Ngọc Phương
VIP
4 tháng 1
\(\left(-4\right)^2.\left(-3\right)-\left[\left(-93\right)+\left(-11+8\right)^3\right]\)
\(=16.\left(-3\right)-\left[\left(-93\right)+\left(-3\right)^3\right]\)
\(=16.\left(-3\right)-\left[\left(-93\right)+-27\right]\)
\(=16.\left(-3\right)-\left(-120\right)\)
\(=-48+120=72\)
VT
4 tháng 1
2011+2012+2013+2014+2015+2016+2017+2018+2019+2020+2021+ 2022+2023 =(2011+2023)+(2013+2022)+...+(2016+2018)+2017 =4034+4034+4034+4034+4034+4034+2017 =4034x6+2017=26221
4 tháng 1
2011+2012+2013+2014+2015+2016+2017+2018+2019+2020+2021+2022+2023
=(2011+2023)+(2013+2022)+...+(2016+2018)+2017 =4034+4034+4034+4034+4034+4034+2017 =4034x6+2017=26221
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
\(S=\dfrac{2}{10.12}+\dfrac{2}{12.14}+\dfrac{2}{14.16}+...+\dfrac{2}{98.100}\)
\(S=\dfrac{1}{10}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{16}+...+\dfrac{1}{98}-\dfrac{1}{100}\)
\(S=\dfrac{1}{10}-\dfrac{1}{100}< \dfrac{1}{10}\) (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 1
a; \(\dfrac{-1}{8}\) + \(\dfrac{-5}{3}\)
= \(\dfrac{-3}{24}\) + \(\dfrac{-40}{24}\)
= \(\dfrac{-43}{24}\)
b; \(\dfrac{-5}{21}\) + \(\dfrac{-2}{21}\) + \(\dfrac{8}{24}\)
= -(\(\dfrac{5}{21}\) + \(\dfrac{2}{21}\)) + \(\dfrac{1}{3}\)
= - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\)
= 0
c; 0,25 + \(\dfrac{5}{6}\) - \(\dfrac{2}{3}\)
= \(\dfrac{1}{4}\) + \(\dfrac{5}{6}\) - \(\dfrac{2}{3}\)
= \(\dfrac{3}{12}\) + \(\dfrac{10}{12}\) - \(\dfrac{8}{12}\)
= \(\dfrac{5}{12}\)
d; \(\dfrac{2}{3}\) - \(\dfrac{5}{7}\).\(\dfrac{14}{25}\)
= \(\dfrac{2}{3}\) - \(\dfrac{2}{5}\)
= \(\dfrac{4}{15}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 1
e; \(\dfrac{-2}{5}\).\(\dfrac{5}{8}\) + \(\dfrac{5}{8}\).\(\dfrac{3}{5}\)
= \(\dfrac{5}{8}\).(\(-\dfrac{2}{5}\) + \(\dfrac{3}{5}\))
= \(\dfrac{5}{8}\).\(\dfrac{1}{5}\)
= \(\dfrac{1}{8}\)
d; \(\dfrac{6}{7}\).\(\dfrac{8}{13}\) + \(\dfrac{6}{13}\).\(\dfrac{9}{7}\) - \(\dfrac{4}{13}\).\(\dfrac{6}{7}\)
= \(\dfrac{6}{7}\).(\(\dfrac{8}{13}\) + \(\dfrac{9}{13}\) - \(\dfrac{4}{13}\))
= \(\dfrac{6}{7}\).\(\dfrac{13}{13}\)
= \(\dfrac{6}{7}\)
TP
1
KV
5 tháng 1
Ta có:
n(n + 1)(n + 2)
= (n² + n)(n + 2)
= n³ + 2n² + n² + 2n
= n³ + 3n² + 2n
Mà n(n + 1)(n + 2) là tích của ba số nguyên liên tiếp (do n là số nguyên)
⇒ n(n + 1)(n + 2) ⋮ 3
⇒ (n³ + 3n² + 2) ⋮ 3
Ta có:
n³ + 11n
= n³ + 3n² + 2n - 3n² + 9n
= (n³ + 3n² + 2n) - 3n(n - 3)
Ta có:
3 ⋮ 3
⇒ 3n(n - 3) ⋮ 3 (với mọi n nguyên)
Mà (n³ + 3n² + 2n) ⋮ 3 (cmt)
⇒ [(n³ + 3n² + 2n) - 3n(n - 3)] ⋮ 3
Vậy (n³ + 11n) ⋮ 3 với mọi số nguyên n
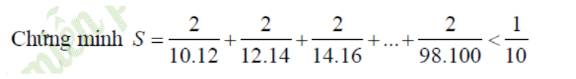
File: undefined