èds

Lời giải:

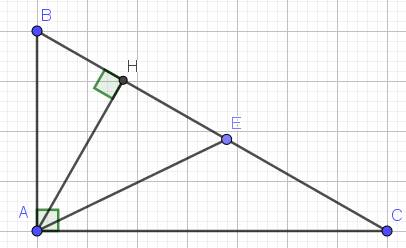
Ta có: $\widehat{BAE}=\widehat{BAC}-\widehat{EAC}$

$=90^0-\frac{1}{2}\widehat{HAC}(1)$

$\widehat{AEB}=\widehat{EAC}+\widehat{ECA}$
$=\frac{1}{2}\widehat{HAC}+(90^0-\widehat{HAC})$

$=90^0-\frac{1}{2}\widehat{HAC}(2)$

Từ $(1); (2)\Rightarrow \widehat{BAE}=\widehat{AEB}$

$\Rightarrow \triangle ABE$ cân tại $B$

Hình vẽ:

1. T

2. F

3. F

4. T

1 T

2 F

3 F

4 T

2 nước và khởi nguyên

3

Lời giải:

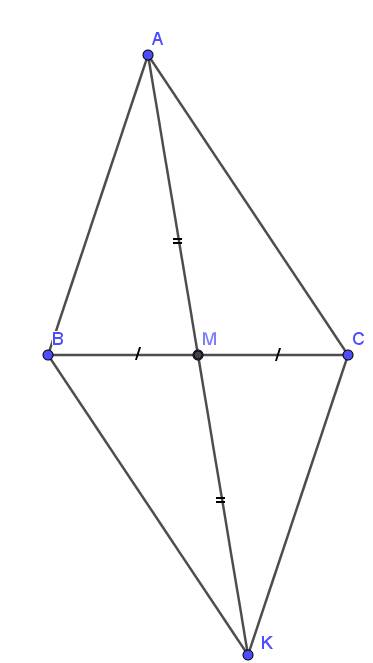
a. Xét tam giác $AMC$ và $KMB$ có:

$MC=MB$ (do $M$ là trung điểm $BC$)

$AM=KM$ (gt)

$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)

$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)

và $\widehat{ACM}=\widehat{KBM}$

Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$

b.

Xét tam giác $ABM$ và $KCM$ có:

$BM=CM$

$AM=KM$

$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)

$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)

$\Rightarrow \widehat{ABM}=\widehat{KCM}$

Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$
 

Hình vẽ:

Để làm được 50 sản phẩm chiếc máy đó cần làm: 30 : 30 x 50 = 50(phút)

Đ/số: 50 phút

Thời gian xe đi hết nửa quãng đường đầu là: \(\dfrac{S}{2}\) : 40 = \(\dfrac{S}{80}\)

Thời gian xe đi hết nửa quãng đường sau là: \(\dfrac{S}{2}\) : 60 = \(\dfrac{S}{120}\)

Thời gian người đó đi trên cả quãng đường là:

       \(\dfrac{S}{80}\) + \(\dfrac{S}{120}\) = \(\dfrac{S}{48}\)

Vận tốc trung bình của người đó trên cả quãng đường là:

    S : \(\dfrac{S}{48}\) = 48 (km/h)

Kết luận:.. 

Áp dụng tính chất dãy tỉ số bằng nhau :

\(\dfrac{x}{2}=\dfrac{y}{-3}=\dfrac{z}{5}=\dfrac{2x+3y+5z}{2.2+3.\left(-3\right)+5.5}=\dfrac{6}{20}=\dfrac{3}{10}\)

\(=>x=\dfrac{3}{10}.2=\dfrac{3}{5}\\ y=\dfrac{3}{10}.\left(-3\right)=-\dfrac{9}{10}\\ z=\dfrac{3}{10}.5=\dfrac{3}{2}\)