Ở đây, có 2 số là 13 và 17 không chia hết cho số nào ngoài 1 và chính nó nên ta chỉ có thể tìm mẫu chung bằng cách nhân các mẫu lại với nhau:

\(MSC=8\cdot13\cdot17=1768\)

A = \(\dfrac{1}{1+2}\) + \(\dfrac{1}{1+2+3}\) + \(\dfrac{1}{1+2+3+4}\)+......+\(\dfrac{1}{1+2+3+....+100}\)

A = \(\dfrac{1}{(1+2)\times2:2}\) + \(\dfrac{1}{(1+3)\times3:2}\) + ......+ \(\dfrac{1}{(1+100)\times100:2}\)

A = \(\dfrac{2}{2\times3}\) + \(\dfrac{2}{3\times4}\)+.....+ \(\dfrac{2}{100\times101}\)

A = 2 \(\times\) ( \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) +....+ \(\dfrac{1}{100\times101}\))

A = 2 \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) +......+ \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\))

A  = 2 \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{101}\))

A = 2 \(\times\) \(\dfrac{99}{202}\)

A = \(\dfrac{99}{101}\)

\(3dm6cm=36cm\)

Từ bài toán, ta có sơ đồ:

Đường chéo lớn: |----| ----|

Đường chéo bé:  |----|

Tổng số phần bằng nhau là:

\(2+1=3\left(phần\right)\)

Giá trị mỗi phần là:

\(36:3=12\left(cm\right)\)

Độ dài đường chéo bé ứng với 1 phần nên độ dài là \(12cm\).

Độ dài đường chéo lớn là:

\(36-12=24\left(cm\right)\)

Diện tích hình thoi là:

\(\dfrac{12\cdot24}{2}=288:2=144\left(cm^2\right)\)

Đáp số: \(144cm^2\)

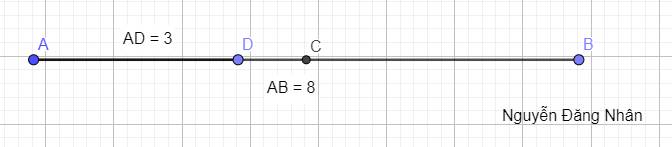
a) Ta có:

\(CA=CB=\dfrac{AB}{2}\) (tính chất trung điểm)

\(\Rightarrow CA=CB=\dfrac{8}{2}=4\left(cm\right)\)

b) D nằm giữa AB nên:

\(DB=AB-AD=8-3=5\left(cm\right)\)

Tương tự, D nằm giữa AC nên:

\(CD=AC-AD=4-3=1\left(cm\right)\)

Đề bài: \(12,5+1,25\cdot55+5\cdot6,25+1,25:0,125+0,5\cdot1,25\)

\(=1.25\cdot10+1,25\cdot55+1,25\cdot5\cdot5+1,25\cdot8+1,25\cdot0,5\)

\(=1,25\cdot\left(10+55+25+8+0,5\right)\)

\(=1,25\cdot98,5\)

\(=123,125\)

Lời giải:

Gọi tổng trên là $A$

$A=\frac{1}{\frac{2\times 3}{2}}+\frac{1}{\frac{3\times 4}{2}}+\frac{1}{\frac{4\times 5}{2}}+...+\frac{1}{\frac{100\times 101}{2}}$

$=\frac{2}{2\times 3}+\frac{2}{3\times 4}+\frac{2}{4\times 5}+....+\frac{2}{100\times 101}$

$=2\times (\frac{1}{2\times 3}+\frac{1}{3\times 4}+\frac{1}{4\times 5}+....+\frac{1}{100\times 101})$

$=2\times (\frac{3-2}{2\times 3}+\frac{4-3}{3\times 4}+\frac{5-4}{4\times 5}+....+\frac{101-100}{100\times 101})$

$=2\times (\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{100}-\frac{1}{101})$

$=2\times (\frac{1}{2}-\frac{1}{101})$

$=1-\frac{2}{101}=\frac{99}{101}$

Là khẳng định A vì ta có thể lấy một số tự nhiên bất kỳ để đặt MSC cho cả a và b và ta lấy phân số nào lớn hơn trừ đi phân số bé hơn