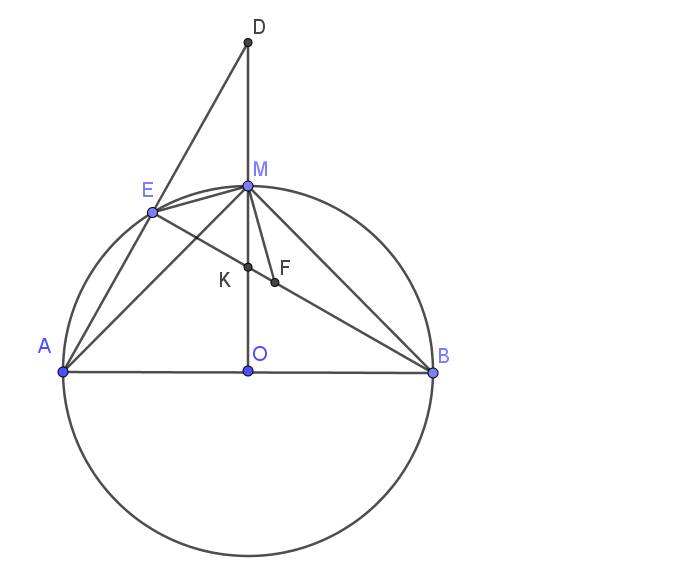
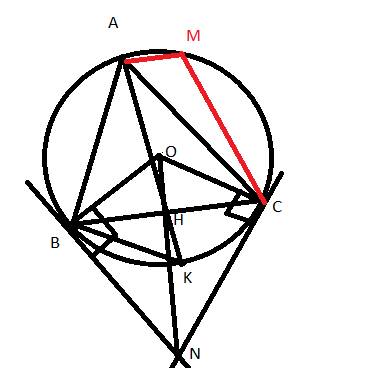
a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

nên MAOB là tứ giác nội tiếp

b: Ta có; ΔOCD cân tại O

mà OK là đường trung tuyến

nên OK\(\perp\)CD tại K

Ta có: \(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)

=>O,K,A,M,B cùng thuộc đường tròn đường kính OM

c: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của BA(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của BA(2)

Từ (1),(2) suy ra OM là đường trung trực của AB

=>OM\(\perp\)AB tại H

Xét ΔOHN vuông tại H và ΔOKM vuông tại K có

\(\widehat{HON}\) chung

Do đó: ΔOHN~ΔOKM

=>\(\dfrac{OH}{OK}=\dfrac{ON}{OM}\)

=>\(OH\cdot OM=OK\cdot ON\left(3\right)\)

Xét ΔOAM vuông tại A có AH là đường cao

nên \(OH\cdot OM=OA^2=R^2\left(4\right)\)

Từ (3),(4) suy ra \(OK\cdot ON=R^2=OD^2\)

=>\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)

Xét ΔOKD và ΔODN có

\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)

\(\widehat{KOD}\) chung

Do đó: ΔOKD~ΔODN

=>\(\widehat{OKD}=\widehat{ODN}=90^0\)

=>ND là tiếp tuyến của (O)

Lời giải:

a.

Vì $M$ là điểm chính giữa cung $AB$ nên $OM\perp AB$

$\Rightarrow \widehat{KOA}=\widehat{MOA}=90^0$

Lại có: $\widehat{AEK}=\widehat{AEB}=90^0$ (góc nt chắn nửa đường tròn)

Xét tứ giác $EAOK$ có tổng hai góc đối nhau $\widehat{KOA}+\widehat{AEK}=90^0+90^0=180^0$

$\Rightarrow EAOK$ là tgnt.

b.

Xét tam giác $EAM$ và $FBM$ có:

$AM=BM$ (do $M$ nằm chính giữa cung AB)

$EA=FB$

$\widehat{EAM}=\widehat{EBM}=\widehat{FBM}$ (góc nt chắn cung $EM$)

$\Rightarrow \triangle EAM=\triangle FBM$ (c.g.c)

$\Rightarrow EM=FM(1)$

Và $\widehat{EMA}=\widehat{FMB}$

$\Rightarrow \widehat{EMA}+\widehat{MAF}=\widehat{FMB}+\widehat{MAF}=\widehat{AMB}=90^0$ (góc nt chắn nửa đường tròn)

$\Rightarrow \widehat{EMF}=90^0(2)$

Từ $(1); (2)$ suy ra $EMF$ là tam giác vuông cân tại $M$

c.

Vì $EMF$ vuông cân tại $M$ nên $\widehat{MEK}=45^0$

$\widehat{DEM}=180^0-\widehat{AEB}-\widehat{MEK}=180^0-90^0-45^0=45^0$

$\Rightarrow \widehat{DEM}=\widehat{MEK}$

$\Rightarrow EM$ là phân giác trong của $\widehat{DEK}$

$\Rightarrow \frac{MK}{MD}=\frac{EK}{ED}$

$\Rightarrow MK.ED=EK.MD$ (đpcm)

Hình vẽ:

Ms lớp 8 nhg lm thử hoii

Gọi số sản phẩm lm trong 1 ngày dự định là x(sản phẩm) 

Số sản phẩm thực tế lm trong 1 ngày : x+10(sản phẩm)

Tổng sản phẩm thực tế: 600+50=650(sản phẩm)

Ta có pt:
\(\dfrac{600}{x}-\dfrac{650}{x+10}=2\)

\(\dfrac{600\left(x+10\right)}{x\left(x+10\right)}-\dfrac{650x}{x\left(x+10\right)}\)\(=\dfrac{2x\left(x+10\right)}{x+10}\)

\(600x+6000-650x=2x^2+20x\)

\(-50x+6000=2x^2+20x\)

\(x^2+35x=3000\)

\(x=40\)

=> Thời gian sx theo hợp đồng= \(\dfrac{600}{40}\)=15 ngày

Quy trình lắp đặt mạch điện hai công tắc ba cực điều khiển một đèn gồm các bước:

- Vạch dấu (1đ)

- Khoan lỗ bảng điện.

- Lắp đặt thiết bị điện của bảng điện.

- Nối dây mạch điện.

- Kiểm tra.

Em tham khảo nhé

https://ipa.khanhhoa.gov.vn/tiem-nang-the-manh