\(e,\dfrac{\sqrt{4x-1}}{\sqrt{7-2x}-2}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}4x-1\ge0\\7-2x\ne4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{4}\\x\ne-\dfrac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{4}\)

\(d,\dfrac{\sqrt{2x-1}}{\sqrt{2x+17}+1}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}2x-1\ge0\\2x+17\ge0\end{matrix}\right.\)  \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ge-\dfrac{17}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{2}\)

 \(b,c,\dfrac{3}{\sqrt{2x-17}}\) có nghĩa \(\Leftrightarrow2x-17>0\Leftrightarrow x>\dfrac{17}{2}\)

\(a,\sqrt{2-5x}\) có nghĩa \(\Leftrightarrow2-5x\ge0\Leftrightarrow x\le\dfrac{2}{5}\)

Hạ đường cao AH của tam giác ABD => AH=14,4cm

Pytago => AD^2-AH^2=DH^2

            => DH^2=116,64

            => DH=10,8cm

HT lượng => HA^2=HB.HC

                => HB=HA^2/HB=14,4^2/10,8=19,2cm

=> BD=HD+HB=10,8+19,2=30m

Pytago => AB^2=AH^2+HB^2=576

            => AB=24cm

=> chu vi HCN ABCD là: 2(AB+AD)=2(18+24)=84(cm^2)

Ta có:

\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)

\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)

\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)

\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)

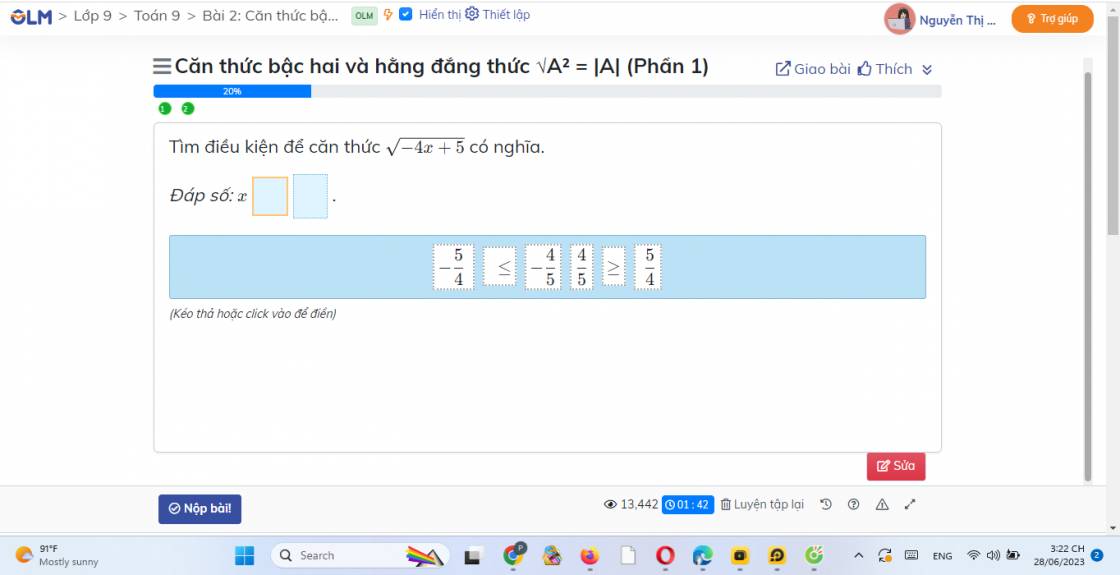
Câu c của em đấy nhé: \(\sqrt{-4x+5}\) có nghĩa ⇔ -4\(x\) + 5 ≥ 0 

                                                                                   4\(x\) ≤ 5 

                                                                                    \(x\) ≤ \(\dfrac{5}{4}\) 

Vậy em kéo dấu ≤ vào ô trống thứ nhất, sau đó em kéo \(\dfrac{5}{4}\) vào ô trống thứ hai rồi ấn nút nộp bài là xong em nhé

\(VT=\dfrac{a}{1+a^2}+\dfrac{b}{1+b^2}=\dfrac{a}{ab+a+b+a^2}+\dfrac{b}{ab+a+b+b^2}\)

\(=\dfrac{a}{\left(a+b\right).\left(a+1\right)}+\dfrac{b}{\left(a+b\right).\left(b+1\right)}\)

\(=\dfrac{\left(a+b\right).\left(ab+a+ab+b\right)}{\left(a+b\right)^2.\left(a+1\right).\left(b+1\right)}=\dfrac{ab+1}{\left(a+b\right).\left(ab+a+b+1\right)}\)

\(=\dfrac{ab+1}{2.\left(a+b\right)}\)(1)

\(VP=\dfrac{ab+1}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{ab+1}{\sqrt{2\left(a+b\right)^2.\left(a+1\right).\left(b+1\right)}}\)

\(=\dfrac{ab+1}{2\left(a+b\right)}\) (2)

Từ (1) (2) => ĐPCM

Giải

Với a,b > 0, ta có:

\(\dfrac{a}{1+a^2}+\dfrac{b}{1+b^2}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\)

Tương đương

\(\dfrac{a+ab^2+b+a^2b}{\left(1+a^2\right)\left(1+b^2\right)}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\\ \Leftrightarrow\dfrac{a+b+ab\left(a+b\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1+ab}{\sqrt{2\left(1+a^2\right)\left(1+b^2\right)}}\\ \Leftrightarrow\dfrac{\left(a+b\right)\left(ab+1\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1+ab}{\sqrt{2}}\\ \Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{\left(1+a^2\right)\left(1+b^2\right)}}=\dfrac{1}{\sqrt{2}}\)

Mặt khác, \(\left(1+a^2\right)\left(1+b^2\right)=\left(a^2+a+b+ab\right)\left(b^2+a+b+ab\right)\\ =\left(a+b\right)\left(a+1\right)\left(a+b\right)\left(b+1\right)\\ =\left(a+b\right)^2\left[\left(a+1\right)\left(b+1\right)\right]\\ =\left(a+b\right)^2\left(a+b+ab+1\right)\\ =2\left(a+b\right)^2\)

Do đó phương trình đã cho tương đương:

\(\Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{2\left(a+b\right)^2}}=\dfrac{1}{\sqrt{2}}\\\Leftrightarrow\dfrac{\left(a+b\right)}{\sqrt{2}.\left(a+b\right)}=\dfrac{1}{\sqrt{2}}\left(a,b>0\right)\\ \Leftrightarrow\dfrac{1}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\left(1\right)\) 

Vì phương trình (1) đúng nên phương trình ban đầu cũng đúng

Suy ra điều phải chứng minh

Mong mn trl mình ạ

Ta có \(x^2+\dfrac{1}{x^2}=7\)

\(\Leftrightarrow x^2+\dfrac{1}{x^2}+2.x.\dfrac{1}{x}=9\)

\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2=9\)

\(\Leftrightarrow x+\dfrac{1}{x}=3\)  (Do x > 0) (1)  

Từ (1) \(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^3=27\Leftrightarrow x^3+\dfrac{1}{x^3}+3.\left(x+\dfrac{1}{x}\right)=27\)

\(\Leftrightarrow x^3+\dfrac{1}{x^3}=18\)

Ta lại có \(\left(x+\dfrac{1}{x}\right)^5=x^5+5x^3+10x+\dfrac{10}{x}+\dfrac{5}{x^3}+\dfrac{1}{x^5}=243\)

\(\Leftrightarrow F=x^5+\dfrac{1}{x^5}=243-5.\left(\dfrac{1}{x^3}+x^3\right)-10.\left(x+\dfrac{1}{x}\right)=123\)

Ta có thể sử dụng công thức Newton về đa thức để giải bài toán này. Đặt đa thức $P(x) = (x-a)(x-b)(x-c) = x^3 - (a+b+c)x^2 + (ab+bc+ca)x - abc$.

Do $a+b+c=0$, nên $P(x) = x^3 - 3kx - abc$ với $k = \frac{ab+bc+ca}{a+b+c}$.

Ta có thể tính được $a^2+b^2+c^2 = -2(ab+bc+ca)$.

Đặt $S_n = a^n + b^n + c^n$. Ta có thể suy ra các công thức sau:

$S_1 = 0$

$S_2 = a^2 + b^2 + c^2 = -2(ab+bc+ca)$

$S_3 = 3abc$

$S_4 = (a^2+b^2+c^2)^2 - 2(a^2b^2+b^2c^2+c^2a^2) = 2(ab+bc+ca)^2 - 3abc(a+b+c)$

$S_5 = 5(ab+bc+ca)(a^2+b^2+c^2) - 5abc(a+b+c)$

$S_6 = (a^2+b^2+c^2)^3 - 3(a^2+b^2+c^2)(a^2b^2+b^2c^2+c^2a^2) + 2(a^2b^2c^2)$

$S_7 = 7(ab+bc+ca)(a^2+b^2+c^2)^2 - 14abc(a^2+b^2+c^2) + 7a^2b^2c^2$

Từ đó, ta có thể tính được $S_1, S_2, S_3, S_4, S_5, S_6$ dựa trên các giá trị đã biết.

Đặt $T_n = a^n+b^n+c^n - S_n$. Ta có thể suy ra các công thức sau:

$T_1 = 0$

$T_2 = 2S_2$

$T_3 = 3S_3$

$T_4 = 2S_2^2 - 4S_4$

$T_5 = 5S_2S_3 - 5S_5$

$T_6 = 2S_2S_4 + 3S_3^2 - 6S_6$

$T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7$

Do $S_1=S_3=0$, nên $T_1=T_3=0$.

Từ $a+b+c=0$, ta có $a^2+b^2+c^2 = -2(ab+bc+ca)$. Do đó, $S_2 = 2(ab+bc+ca)$ và $S_4 = 2(ab+bc+ca)^2 - 3abc(a+b+c) = 2(ab+bc+ca)^2$.

Từ $a^7+b^7+c^7=0$, ta có $T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7 = 7S_2S_5 - 14S_4S_3 + 7S_7 = 7S_7$.

Từ $T_7 = 7S_7$, ta có $S_7 = \frac{T_7}{7} = 0$.

Do đó, $T_6 = 2S_2S_4 + 3S_3^2 - 6S_6 = 2(2(ab+bc+ca))(2(ab+bc+ca)^2) + 3(abc)^2 - 6S_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$.

Từ $T_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$, ta có $S_6 = \frac{1}{6}(12(ab+bc+ca)^2 + 3(abc

Giải

Vì a + b + c = 0 nên a + b = -c

Ta có:

\(a^7+b^7=\left(a+b\right)\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =-c\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =c\left(-a^6+a^5b-a^4b^2+a^3b^3-a^2b^4+ab^5-b^6\right)\\ =c\left[-\left(a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6\right)+\left(7a^5b+14a^4b^2+21a^3b^3+14a^2b^4+7ab^5\right)\right]\\ =c\left[-\left(a+b\right)^6+7ab\left(a^4+2a^3b+3a^2b^2+2ab^3+b^4\right)\right]\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)^2+2ab\left(a^2+b^2\right)+3a^2b^2-2a^2b^2\right]\right\}\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =c\left\{-c^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =-c^7+7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\\ \Rightarrow a^7+b^7+c^7=7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\Rightarrow7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]=0\)TH1: \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2=0\)

Vì \(a^2,b^2,\left(a+b\right)^2,a^2b^2\ge0\) nên \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\ge0\)

Dấu "=" xảy ra khi và chỉ khi a = b = 0

Mà a + b + c = 0 nên suy ra c = 0

Vậy \(a^{2023}+b^{2023}+c^{2023}=0\)

TH2: abc = 0

Vì abc = 0 nên sẽ có ít nhất một trong ba số a, b, c = 0

Vì a, b, c có vai trò như nhau nên không mất tính tổng quát, giả sử \(c=0\)

Mà a + b + c = 0 nên a + b =0 hay a = -b

\(\Rightarrow a^{2023}+b^{2023}+c^{2023}=0\)

Kết luận: \(a^{2023}+b^{2023}+c^{2023}=0\)

Lời giải:

ĐK: $3m+1\neq 0$

Gọi $A,B$ lần lượt là giao điểm của $(d)$ với $Ox,Oy$

Vì $A\in Ox$ nên $y_A=0$

$y_A=(3m+1)x_A-6m-1=0$

$\Rightarrow x_A=\frac{6m+1}{3m+1}$

Vậy $A(\frac{6m+1}{3m+1},0)$

Tương tự: $B(0, -6m-1)$

Gọi $h$ là khoảng cách từ $O$ đến $(d)$

Khi đó, theo hệ thức lượng trong tam giác vuông ta có:

$\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}$

$=\frac{1}{|x_A|^2}+\frac{1}{|y_B|^2}$

$=\frac{(3m+1)^2}{(6m+1)^2}+\frac{1}{(6m+1)^2}$
$=\frac{(3m+1)^2+1}{(6m+1)^2}$

Để $h$ max thì $\frac{1}{h^2}$ min 

Hay $\frac{(3m+1)^2+1}{(6m+1)^2}$ min

Áp dụng BĐT Bunhiacopxky:

$[(3m+1)^2+1][2^2+(-1)^2]\geq [2(3m+1)+(-1)]^2=(6m+1)^2$
$\Rightarrow 5[(3m+1)^2+1]\geq (6m+1)^2$

$\Rightarrow \frac{1}{h^2}\geq \frac{1}{5}$

Giá trị này đạt tại $\frac{3m+1}{2}=\frac{1}{-1}$

$\Leftrightarrow m=-1$

\(3,\dfrac{\sqrt{9+6\sqrt{2}}}{\sqrt{3}}\)

\(=\dfrac{\sqrt{3\left(3+2\sqrt{2}\right)}}{\sqrt{3}}\)

\(=\dfrac{\sqrt{3}.\sqrt{3+2\sqrt{2}}}{\sqrt{3}}\)

\(=\sqrt{3+2\sqrt{2}}\)

\(=\sqrt{\sqrt{2^2}+2\sqrt{2}+1}\)

\(=\sqrt{\left(\sqrt{2}+1\right)^2}\)

\(=\left|\sqrt{2}+1\right|=\sqrt{2}+1\)

\(4,\sqrt{2+\sqrt{3}}:\sqrt{\dfrac{1}{2}}\)

\(=\sqrt{2+\sqrt{3}}:\dfrac{1}{\sqrt{2}}\)

\(=\sqrt{2+\sqrt{3}}.\sqrt{2}\)

\(=\sqrt{4+2\sqrt{3}}\)

\(=\sqrt{\sqrt{3^2}+2\sqrt{3}+1}\)

\(=\sqrt{\left(\sqrt{3}+1\right)}^2\)

\(=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)

Cặp \(m=2\) , \(n=1\) vẫn thỏa \(m^2-2020n^2+2022⋮mn\)

Để chứng minh rằng m và n là hai số lẻ và nguyên tố cùng nhau, ta cần thực hiện các bước sau đây:

Bước 1: Giả sử rằng m và n là hai số tự nhiên thỏa mãn m^2 - 2020n^2 + 2022 chia hết cho mn.

Bước 2: Ta sẽ chứng minh rằng m và n là hai số lẻ.

Giả sử rằng m là số chẵn, tức là m = 2k với k là một số tự nhiên. Thay thế vào biểu thức ban đầu, ta có:

(2k)^2 - 2020n^2 + 2022 chia hết cho 2kn

Simplifying the equation, we get:

4k^2 - 2020n^2 + 2022 chia hết cho 2kn

Dividing both sides by 2, we have:

2k^2 - 1010n^2 + 1011 chia hết cho kn

Do 2k^2 chia hết cho kn, vì vậy 2k^2 cũng chia hết cho kn. Từ đó, 1011 chia hết cho kn.

Bởi vì 1011 là một số lẻ, để 1011 chia hết cho kn, thì kn cũng phải là một số lẻ. Vì vậy, n cũng phải là số lẻ.

Do đó, giả sử m là số chẵn là không hợp lệ. Vậy m phải là số lẻ.

Bước 3: Chứng minh rằng m và n là hai số nguyên tố cùng nhau.

Giả sử rằng m và n không phải là hai số nguyên tố cùng nhau. Điều đó có nghĩa là tồn tại một số nguyên tố p chia hết cả m và n.

Vì m là số lẻ, n là số lẻ và p là số nguyên tố chia hết cả m và n, vì vậy p không thể chia hết cho 2.

Ta biểu diễn m^2 - 2020n^2 + 2022 dưới dạng phân tích nhân tử:

m^2 - 2020n^2 + 2022 = (m - n√2020)(m + n√2020)

Vì p chia hết cả m và n, p cũng phải chia hết cho (m - n√2020) và (m + n√2020).

Tuy nhiên, ta thấy rằng (m - n√2020) và (m + n√2020) không thể cùng chia hết cho số nguyên tố p, vì chúng có dạng khác nhau (một dạng có căn bậc hai và một dạng không có căn bậc hai).

Điều này dẫn đến mâu thuẫn, do đó giả sử ban đầu là sai.

Vậy ta có kết luận rằng m và n là hai số tự nhiên lẻ và nguyên tố cùng nhau.