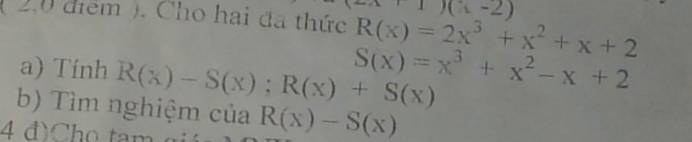
a) Do ∆ABC cân tại A (gt)

⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2

= (180⁰ - 45⁰) : 2

= 67,5⁰

Do ∠ABC = ∠ACB > ∠BAC (67,5⁰ = 67,5⁰ > 45⁰)

⇒ AC = AB > BC

b) Do ∠ABC = ∠ACB (cmt)

⇒ ∠DBC = ∠ECB

Xét ∆BCD và ∆CBE có:

BD = CE (gt)

∠DBC = ∠ECB (cmt)

BC là cạnh chung

⇒ ∆BCD = ∆CBE (c-g-c)

⇒ ∠BDC = ∠CEB (hai góc tương ứng)

tính góc tới,góc phản xạ:

50 : 2 =25

i=i'=25 độ

When I passed college, my dad bought me a motorbike. It was a white Wave car. I really love it. The motorbike has a plastic shell. The saddle is designed long and wide, very smooth. It has one brake in the right hand and one brake in the right foot for operator convenience. The front has a headlight, I can adjust the height or low of the lights. The turn signal light switch is designed on the right hand side, we will push the control button to turn on the turn signal light on the corresponding side. The body of the motorcycle has a stainless steel frame that allows us to grip small items that are not needed. Besides, there are 2 very convenient fasteners. The bottom of the motorcycle saddle has a small trunk where you can put your raincoat or sunscreen. The gas compartment is also located here. When the fuel tank is filled, the car can run 200km. When traveling by motorbike in Vietnam, you need to be 18 years old and have a driver’s license. Because the roads in Vietnam are not too big, traveling by motorbike makes it easy to slip through obstacles. However, motorbikes also have some limitations such as smog. However, the effects it gives still make me want to use it.

a) Do ND là đường phân giác của ∆MNP (gt)

⇒ ∠MND = ∠PND

⇒ ∠MND = ∠HND

Xét hai tam giác vuông: ∆MND và ∆HND có:

ND là cạnh chung

∠MND = ∠HND (cmt)

⇒ ∆MND = ∆HND (cạnh huyền - góc nhọn)

b) Do ∆MND = ∆HND (cmt)

⇒ MN = HN (hai cạnh tương ứng)

c) Do ∆MND = ∆HND (cmt)

⇒ MD = HD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆DMK và ∆DHP có:

MD = HD (cmt)

∠MDK = ∠HDP (đối đỉnh)

⇒ ∆DMK = ∆DHP (cạnh góc vuông - góc nhọn kề)

⇒ MK = HP (hai cạnh tương ứng)

Lại có: MN = HN (cmt)

⇒ MK + MN = HP + HN

⇒ KN = PN

⇒ ∆NPK cân tại N

Do ∆MNP vuông tại M (gt)

⇒ PM ⊥ MN

⇒ PM ⊥ NK

⇒ PM là đường cao của ∆NPK

Lại có:

DH ⊥ NP (gt)

⇒ KH ⊥ NP

⇒ KH là đường cao thứ hai của ∆NPK

⇒ ND là đường cao thứ ba của ∆NPK

Mà ∆NPK cân tại N (cmt)

⇒ ND cũng là đường trung tuyến của ∆NPK

⇒ ND đi qua trung điểm của PK

Mà I là trung điểm của PK

⇒ N, D, I thẳng hàng

a: A(x)+B(x)

\(=8x^4+8x^3-6x-15+8x^4+8x^3-4x^2-6x-10\)

\(=16x^4+16x^3-4x^2-12x-25\)

b: B(x)-A(x)

\(=8x^4+8x^3-4x^2-6x-10-8x^4-8x^3+6x+15\)

\(=-4x^2+5\)

c: \(C\left(x\right)\cdot\left(B\left(x\right)-A\left(x\right)\right)=\left(x+1\right)\left(-4x^2+5\right)\)

\(=-4x^3+5x-4x^2+5\)

Công thức tính diện tích đáy của hình lăng trụ đứng còn tùy thuộc xem đáy của hình lăng trụ đứng đó là hình gì em nhé.

+ Nếu đáy là hình tam giác sử dụng công thức tính diện tích hình tam giác

+ Nếu đáy là hình chữ nhật sử dụng công thức tính diện tích hình chữ nhật

+ Nếu đáy là hình thang sử dụng công thức tính diện tích hình thang.

+ Nếu đáy là hình tròn sử dụng công thức tính diện tích hình tròn.

+ Nếu đáy là hình vuông sử dụng công thức tính diện tích hình vuông.

+ Nếu đáy là hình thoi sử dụng công thức tính diện tích hình thoi.

+ Nếu đáy là bình hành thì sử dụng công thức tính diện tích hình bình hành.

+ Nếu đáy là hình khác biệt thì chia đáy đó thành hình thông thường, tính diện tích từng hình, cộng tất cả diện tích các hình thông thường đó ta được diện tích đáy. 

Công thức tính diện tích đáy của hình lăng trụ đứng còn tùy thuộc xem đáy của hình lăng trụ đứng đó là hình gì em nhé.

+ Nếu đáy là hình tam giác sử dụng công thức tính diện tích hình tam giác

+ Nếu đáy là hình chữ nhật sử dụng công thức tính diện tích hình chữ nhật

+ Nếu đáy là hình thang sử dụng công thức tính diện tích hình thang.

+ Nếu đáy là hình tròn sử dụng công thức tính diện tích hình tròn.

+ Nếu đáy là hình vuông sử dụng công thức tính diện tích hình vuông.

+ Nếu đáy là hình thoi sử dụng công thức tính diện tích hình thoi.

+ Nếu đáy là bình hành thì sử dụng công thức tính diện tích hình bình hành.

+ Nếu đáy là hình khác biệt thì chia đáy đó thành hình thông thường, tính diện tích từng hình, cộng tất cả diện tích các hình thông thường đó ta được diện tích đáy. 

1. Tôn trọng và hiểu biết về văn hóa, truyền thống của các dân tộc: Tìm hiểu về nền văn hóa, lịch sử, và truyền thống của các dân tộc trong địa phương. Tôn trọng và hiểu biết sâu sắc về những điều này sẽ giúp tạo ra một môi trường tôn trọng và đa dạng.

2. Tương tác tích cực và hòa đồng với mọi người: Hãy tạo ra các cơ hội để tương tác và giao tiếp với các thành viên của các dân tộc khác nhau. Để hiểu và đánh giá các quan điểm và trải nghiệm của họ, bạn có thể tham gia vào các hoạt động cộng đồng, sự kiện văn hóa, hay các khóa học về đa văn hóa.

3. Chia sẻ kiến thức và kinh nghiệm của bản thân: Nếu bạn có kiến thức hoặc kinh nghiệm đặc biệt, hãy chia sẻ chúng với người khác trong cộng đồng. Điều này không chỉ giúp tăng cường tinh thần đoàn kết mà còn tạo ra sự đồng thuận và hiểu biết.

4. Tham gia vào các hoạt động cộng đồng và dự án chung: Tham gia vào các dự án hoặc hoạt động mà các dân tộc tham gia cùng nhau có thể tạo ra cơ hội để xây dựng tinh thần đoàn kết và sự hiểu biết lẫn nhau.

5. Tránh đối xử phân biệt và kích động: Tránh các hành vi hoặc lời nói gây mất tôn trọng hoặc gây khó khăn cho bất kỳ dân tộc nào. Thay vào đó, hãy thể hiện sự tôn trọng và sẵn lòng học hỏi từ những người khác.

Px = 3x mũ 5 + 4x mũ 4 - 2x mũ 3 -                    5

- 

Qx = - 3x mũ 5 - 4x mũ 4 + 2x mũ 3 - 3x mũ 2 + 1

----------------------------------------------------------------------------

Px + Qx = 6x mũ 5 + 8x mũ 4 - 4x mũ 3 -2x mũ + 3x mũ 2 + 4

b, ???

nói giải thích cụ thể đi bạn 

a: R(x)-S(x)

\(=2x^3+x^2+x+2-x^3-x^2+x-2\)

\(=x^3+2x\)

R(x)+S(x)

\(=2x^3+x^2+x+2+x^3+x^2-x+2\)

\(=3x^3+2x^2+4\)

b: Đặt R(x)-S(x)=0

=>\(x^3+2x=0\)

=>\(x\left(x^2+2\right)=0\)

mà \(x^2+2>=2>0\forall x\)

nên x=0