
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d, -(24 - 87) + (- 87 + 48 - 24)
= - 24 + 87 - 87 + 48 - 24
= - (24 + 24) + (87 - 87 ) + 48
= -48 + 0 + 48
= 0
e, (2027. 20262024 - 20262024) : 20262025
= 20262024.(2027 - 1):20262025
= 20262024.2026: 20262025
= 20262025:20262025
= 1

35×(52−103)−58:(14−23)35×(52-103)-58:(14-23)
=35×(156−206)−58:(312−812)=35×(156-206)-58:(312-812)
=35×(−56)−58:(−512)=35×(-56)-58:(-512)
=−12−(−32)=-12-(-32)
=−12+32=-12+32
=22=22
=1

\(A=\dfrac{10}{7.12}+\dfrac{10}{12.17}+\dfrac{10}{17.22}+...+\dfrac{10}{502.507}\) (sửa 502+507 thành 503.507)
\(\Rightarrow A=10\left(\dfrac{1}{7.12}+\dfrac{1}{12.17}+\dfrac{1}{17.22}+...+\dfrac{1}{502.507}\right)\)
\(\Rightarrow A=10.\dfrac{1}{5}\left(\dfrac{1}{7}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{22}+...+\dfrac{1}{502}-\dfrac{1}{507}\right)\)
\(\Rightarrow A=2.\left(\dfrac{1}{7}-\dfrac{1}{507}\right)=2.\left(\dfrac{500}{3549}\right)=\dfrac{1000}{3549}\)
\(B=\dfrac{4}{8.13}+\dfrac{4}{13.18}+\dfrac{4}{18.23}+...+\dfrac{4}{253.258}\)
\(\Rightarrow B=4\left(\dfrac{1}{8.13}+\dfrac{1}{13.18}+\dfrac{1}{18.23}+...+\dfrac{1}{253.258}\right)\)
\(\Rightarrow B=4.\dfrac{1}{5}\left(\dfrac{1}{8}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{23}+...+\dfrac{1}{253}-\dfrac{1}{258}\right)\)
\(\Rightarrow B=\dfrac{4}{5}\left(\dfrac{1}{8}-\dfrac{1}{258}\right)=\dfrac{4}{5}\left(\dfrac{129}{1032}-\dfrac{8}{1032}\right)=\dfrac{4}{5}.\dfrac{121}{1032}=\dfrac{121}{1290}\)

\(x\left(x-y\right)=\dfrac{10}{9}\) (1)
\(y\left(x-y\right)=\dfrac{-2}{3}\) (2)
Trừ 1 và 2, ta được:
\(x\left(x-y\right)-y\left(x-y\right)=\dfrac{10}{9}-\left(\dfrac{-2}{3}\right)\)
\(\left(x-y\right)\times\left(x-y\right)=\dfrac{16}{9}\)
\(\left(x-y\right)^2=\left(\pm\dfrac{4}{3}\right)^2\)
=> \(x-y=\pm\dfrac{4}{3}\)
TH1:
Nếu \(x-y=\dfrac{4}{3}\) thay vào 1 và 2, Ta có:
\(x\times\dfrac{4}{3}=\dfrac{10}{9}\) => \(x=\dfrac{10}{9}\div\dfrac{4}{3}\) => \(x=\dfrac{5}{6}\)
\(y\times\dfrac{4}{3}=\dfrac{-2}{3}\) => \(y=\dfrac{-2}{3}\div\dfrac{4}{3}\) => \(y=-\dfrac{1}{2}\)
TH2:
+) Nếu \(x-y=-\dfrac{4}{3}\) thay vào 1 và 2, ta được:
\(x\times\dfrac{-4}{3}=\dfrac{10}{9}\) => \(x=\dfrac{10}{9}\div\dfrac{-4}{3}=\dfrac{-5}{6}\)
\(y\times\dfrac{-4}{3}=\dfrac{-2}{3}\) => \(y=\dfrac{-2}{3}\div\dfrac{-4}{3}=\dfrac{1}{2}\)
Vậy ta có 2 cặp số (x,y) thoả mãn là \(\left(\dfrac{5}{6},\dfrac{-1}{2}\right);\left(\dfrac{-5}{6},\dfrac{1}{2}\right)\)

a) \(8,5.2,3+3,7.4,2=9.2+4.4=18+16=34\)
b) \(2,6.\left(15,245+84,564\right)=3.\left(15+85\right)=2.100=300\)
c) \(5,37.12,8:24,56=5.13:25=\dfrac{13}{5}\)

\(\dfrac{x-1}{11}\) + \(\dfrac{x-2}{10}\) = \(\dfrac{x-3}{9}\) + \(\dfrac{x-4}{8}\)
\(\dfrac{x-1}{11}\) - 1 + \(\dfrac{x-2}{10}\) - 1 = \(\dfrac{x-3}{9}\) - 1 + \(\dfrac{x-4}{8}\)
\(\dfrac{x-12}{11}\) + \(\dfrac{x-12}{10}\) = \(\dfrac{x-12}{9}\) + \(\dfrac{x-12}{8}\)
(\(x-12\)).( \(\dfrac{1}{11}\) + \(\dfrac{1}{10}\)) = (\(x-12\)) (\(\dfrac{1}{9}\) + \(\dfrac{1}{8}\))
(\(x\) - 12).( \(\dfrac{1}{11}\) + \(\dfrac{1}{10}\) - \(\dfrac{1}{9}\) - \(\dfrac{1}{8}\)) = 0
\(x-12\) = 0
\(x\) = 12

Đặt \(x=\dfrac{1}{49\cdot44}+\dfrac{1}{44\cdot39}+...+\dfrac{1}{14\cdot9}+\dfrac{1}{9\cdot4}\) và y = ... (thừa số thứ hai chưa ghi rõ, nếu ghi rõ thì mới làm được)
Ta có:
\(5x=5\left(\dfrac{1}{49\cdot44}+\dfrac{1}{44\cdot39}+...+\dfrac{1}{14\cdot9}+\dfrac{1}{9\cdot4}\right)\)
\(5x=\dfrac{5}{49\cdot44}+\dfrac{5}{44\cdot39}+...+\dfrac{5}{14\cdot9}+\dfrac{5}{9\cdot4}\)
\(5x=\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{39}-\dfrac{1}{44}+\dfrac{1}{44}-\dfrac{1}{49}\)
\(5x=\dfrac{1}{4}-\dfrac{1}{49}=\dfrac{45}{196}\)
\(x=\dfrac{45}{196}\div5=\dfrac{9}{196}\)
Từ đây tự tìm y (thừa số thứ hai)
Suy ra \(A=xy=\dfrac{9}{196}\cdot...=...\)

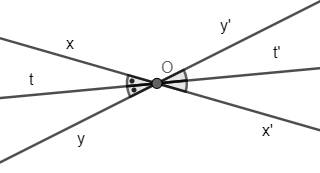
Theo đề ta có:
\(\widehat{tOx}+\widehat{t'Oy'}+\widehat{xOy'}=\dfrac{1}{2}\widehat{xOy}+\dfrac{1}{2}\widehat{x'Oy'}+\widehat{xOy'}\)
Mà \(\widehat{xOy}=\widehat{x'Oy'}\) (hai góc đối đỉnh)
Suy ra biểu thức trên bằng \(\widehat{xOy}+\widehat{xOy'}=180^o\) (hai góc kề bù)
Hay \(\widehat{tOx}+\widehat{t'Oy'}+\widehat{xOy'}=\widehat{tOt'}=180^o\)
Từ đó suy ra tt' là một góc bẹt, hay tia Ot và tia Ot' là hai tia đối nhau
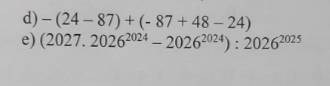
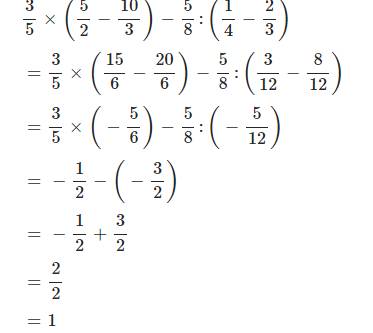
Cần gấp
Để olm.vn giúp em, em nhé.
Kẻ AB kéo dài về phía B cắt đường thẳng y tại L
Kéo dài CB vế phía B cắt đường thẳng x tại M
Vì x//y ta có: \(\widehat{MAB}\) = \(\widehat{BLC}\) ( so le trong)
\(\widehat{ABC}\) = \(\widehat{BCL}\) + \(\widehat{BLC}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
⇒ \(\widehat{ABC}\) = \(\widehat{BCL}\) + \(\widehat{MAB}\) (đpcm)