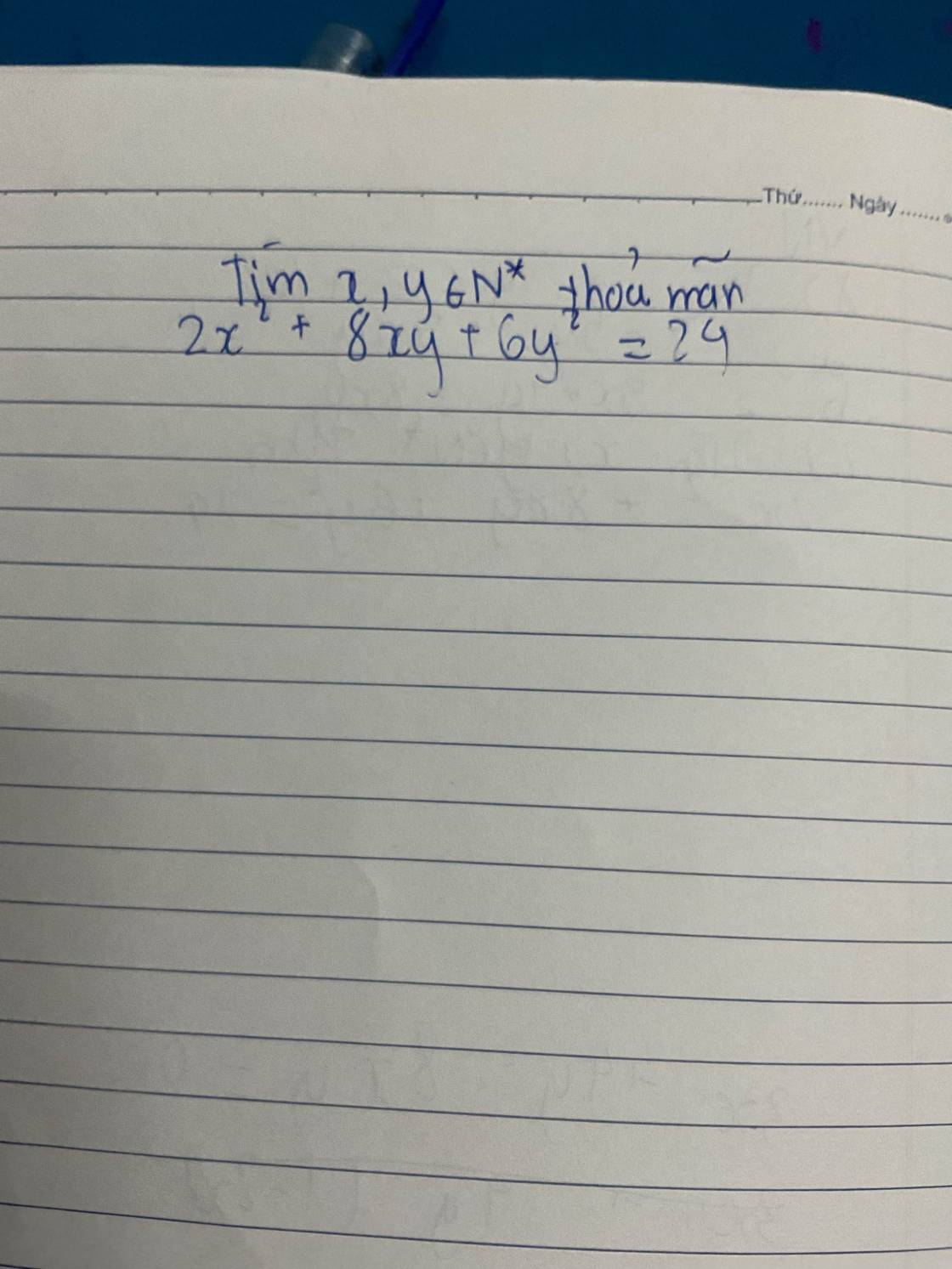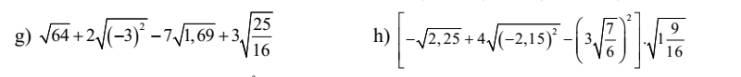a) Thể tích hình hộp bị khuyết :

\(4.4.4=4^3=64\left(cm^3\right)\)

b) Diện tích xung quanh hình hộp bị khuyết (3 mặt)

\(3.4.4.4=192\left(cm^2\right)\)

làm như bạn trí là đúng nhé

\(2x^2+8xy+6y^2=24\left(x;y\inℕ^∗\right)\)

\(\Rightarrow2\left(x^2+4xy+3y^2\right)=24\)

\(\Rightarrow\left(x^2+4xy+4y^2\right)-y^2=12\)

\(\Rightarrow\left(x+2y\right)^2-y^2=12\)

\(\Rightarrow\left(x+2y+y\right)\left(x+2y-y\right)=12\)

\(\Rightarrow\left(x+3y\right)\left(x+y\right)=12\)

\(\Rightarrow\left(x+3y\right);\left(x+y\right)\in\left\{1;2;3;4;6;12\right\}\)

\(\Rightarrow\left(x+3y\right);\left(x+y\right)\in\left\{1;2;3;4;6;12\right\}\)

Ta giải các hệ phương trình sau :

1) \(\left\{{}\begin{matrix}x+3y=1\\x+y=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y=-11\left(loại\right)\\x+y=12\end{matrix}\right.\)

2) \(\left\{{}\begin{matrix}x+3y=2\\x+y=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y=-3\left(loại\right)\\x+y=6\end{matrix}\right.\)

3) \(\left\{{}\begin{matrix}x+3y=3\\x+y=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y=-1\left(loại\right)\\x+y=4\end{matrix}\right.\)

4) \(\left\{{}\begin{matrix}x+3y=4\\x+y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y=1\left(loại\right)\\x+y=3\end{matrix}\right.\)

5) \(\left\{{}\begin{matrix}x+3y=6\\x+y=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y=4\\x+y=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=2\\x=0\left(loại\right)\end{matrix}\right.\)

6) \(\left\{{}\begin{matrix}x+3y=12\\x+y=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y=11\left(loại\right)\\x+y=1\end{matrix}\right.\)

Vậy \(\left(x;y\right)\in\left\{\varnothing\right\}\)

\(\dfrac{3^6.45^4-15^{13}.5^{-9}}{27^4.25^3+45^6}=\dfrac{3^6.3^85^4-3^{13}.5^{13}.5^{-9}}{3^{12}.5^6+3^{12}.5^6}\)

\(=\dfrac{3^{14}.5^4-3^{13}.5^4}{2.3^{12}.5^6}=\dfrac{3^{13}.5^4\left(3-1\right)}{2.3^{12}.5^6}\)

\(=\dfrac{3.2}{2.5^2}=\dfrac{3}{25}\)

\(4x=5y\Rightarrow x=\dfrac{5}{4}y\\ \Rightarrow\dfrac{15}{4}y-2y=5\\ \Leftrightarrow\dfrac{7}{4}y=5\\ y=\dfrac{20}{7}\\ \Rightarrow x=\dfrac{25}{7}\)

Bằng 25/7 bạn nhé

\(\left[-\sqrt{2,25}+4\sqrt{\left(-2,15\right)^2}-\left(3\sqrt{\dfrac{7}{6}}\right)^2\right]\sqrt{1\dfrac{9}{16}}\)

\(=\left[-1,5+4\sqrt{2,15^2}-9\cdot\dfrac{7}{6}\right]\sqrt{\dfrac{25}{16}}\)

\(=\left[4\cdot\dfrac{43}{20}-10,5-1,5\right]\cdot\dfrac{5}{4}\)

\(=\left[\dfrac{43}{5}-12\right]\cdot\dfrac{5}{4}\)

\(=\dfrac{43}{5}\cdot\dfrac{5}{4}-12\cdot\dfrac{5}{4}\)

\(=\dfrac{43}{4}-15=\dfrac{-17}{4}\)

g) \(\sqrt[]{64}+2\sqrt[]{\left(-3\right)^2}-7\sqrt[]{1,69}+3\sqrt[]{\dfrac{25}{16}}\)

\(=8+2.3-7.1,3+3.\dfrac{5}{4}\)

\(=14-9,1+\dfrac{15}{4}\)

\(=5,1+3,75=8,85\)

ko tính đc

số âm ko có căn bậc 2 số học

\(\sqrt[]{2^2+\sqrt[]{4^2}+\sqrt[]{\left(-6\right)^2}+\sqrt[]{\left(-8\right)^2}}\)

\(=\sqrt[]{4+4+6+8}=\sqrt[]{22}\)

\(a=2022.\left|x^2+1\right|+2023\)

\(\Rightarrow a=2022.\left(x^2+1\right)+2023\left(\left|x^2+1\right|>0,\forall x\right)\)

mà \(\left(x^2+1\right)\ge1,\forall x\)

\(\Rightarrow a=2022.\left(x^2+1\right)+2023\ge2022.1+2023=4045\)

\(\Rightarrow GTNN\left(a\right)=4045\left(x=0\right)\)

GTNN(a) = 4045 khi x = 0