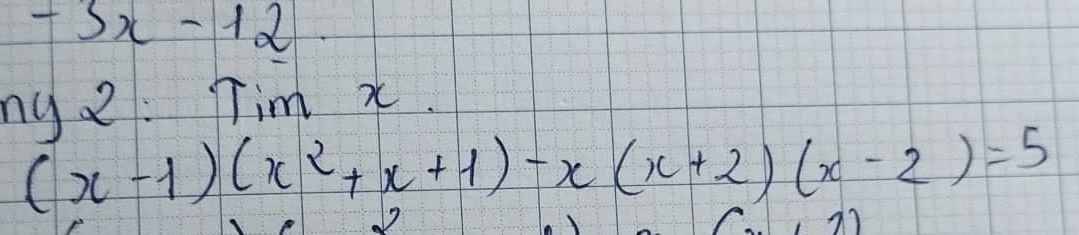\(A=\left(\dfrac{x^2}{x^3-4x}+\dfrac{6}{6-3x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)

\(ĐK:x\ne0;2;-2\)

\(A=\left(\dfrac{x^2}{x\left(x^2-4\right)}+\dfrac{6}{3\left(2-x\right)}+\dfrac{1}{x+2}\right):\left(\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)

\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(\dfrac{x^2-4+10-x^2}{x+2}\right)\)

\(A=\left(\dfrac{x-2\left(x+2\right)+\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{6}{x+2}\right)\)

\(A=\dfrac{x-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{6}\)

\(A=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}.\dfrac{x+2}{6}\)

\(A=-\dfrac{1}{x-2}\)

`a)(2x-3y)(x-2y)`

`=2x^2-4xy-3xy+6y^2=2x^2-7xy+6^2`

`b)(3x+2)^2-(x-1)(2x-3)`

`=9x^2+12x+4-2x^2+3x+2x-3=7x^2+17x+1`

`c)(x-2)^2-3(x-3)(x+3)-(x-2)`

`=x^2-4x+4-3x^2+27-x+2`

`=-2x^2-5x+33`

`a)`\(\left(2x-3y\right)\left(x-2y\right)=2x^2-4xy-3xy+6y^2=2x^2-7xy+6y^2\)

`b)`\(\left(3x+2\right)^2-\left(x-1\right)\left(2x-3\right)=9x^2+12x+4-\left(2x^2-3x-2x+3\right)=7x^2+17x+1\)

`c)`

\(\left(x-2\right)^2-3\left(x-3\right)\left(x+3\right)-\left(x-2\right)=x^2-4x+4-3x^2+27-x+2=-2x^2-5x+33\)

\(\left(x-1\right)\left(x^2+x+1\right)-x\left(x+2\right)\left(x-2\right)=5\)

\(\Leftrightarrow x^3-1-x\left(x^2-4\right)=5\)

\(\Leftrightarrow x^3-1-x^3+4x=5\)

\(\Leftrightarrow4x=6\)

`<=>x=3/2`

Vậy \(S=\left\{\dfrac{3}{2}\right\}\)

`x^2-2x >= 0`

`<=>x(x-2) >= 0`

`<=>` $\left[\begin{matrix} \begin{cases} x \ge 0\\x-2 \ge 0 \end{cases}\\ \begin{cases} x \le 0\\x-2 \le 0 \end{cases}\end{matrix}\right.$

`<=>` $\left[\begin{matrix} \begin{cases} x \ge 0\\x \ge 2 \end{cases}\\ \begin{cases} x \le 0\\x \le 2 \end{cases}\end{matrix}\right.$

`<=>` $\left[\begin{matrix} x \ge 2\\ x \le 0\end{matrix}\right.$

Vậy `S={x|x >= 2;x <= 0}`

\(x^2-2x\ge0\Leftrightarrow x\left(x-2\right)\ge0\)

\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x-2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x-2< 0\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x\ge2\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x< 2\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x\ge2\\x< 0\end{matrix}\right.\)

\(x\left(x+3\right)-2\left(-5+1\right)x=x^2-3\left(4-2x\right)\)

\(\Leftrightarrow x\left(x+3\right)-2x\left(-5+1\right)=x^2-3\left(4-2x\right)\)

\(\Leftrightarrow x^2+3x+10x-2x=x^2-12+6x\)

\(\Leftrightarrow x^2+11x=x^2+6x-12\)

\(\Leftrightarrow5x+12=0\)

\(\Leftrightarrow x=-\dfrac{12}{5}\)

`x(x+3)-2(-5+1)x=x^2-3(4-2x)`

`=>x^2+3x+10-2x=x^2-12+6x`

`=>x^2+3x+10-2x-x^2+12-6x=0`

`=>-5x+20=0`

`=>-5x=-20`

`=>x=(-20)/(-5)`

`=>x=4`

- Albert biết tháng sinh của Cheryl và khẳng định B cũng không biết chứng tỏ C không phải sinh tháng 6 vì nhỡ ngày sinh của C là ngày 18 thì là ngày duy nhất xuất hiện trong 10 đáp án thì B sẽ đoán ngay ra ngày sinh của C là 18/6)

- Khi nghe A nói thì B đoán được ngay ngày sinh của C vậy C phải sinh ngày 17/8 vì sau khi loại đi hai đáp án là ngày 17/6 và 18/6 thì chỉ còn ngày 17 là ngày xuất hiện duy nhất trong 8 đáp án còn lại