Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P\left(1\right)=1^3-2\cdot a\cdot1+a^2=a^2-2a+1\)
\(Q\left(3\right)=3^2+\left(3a+1\right)\cdot3+a^2=a^2+9a+12\)
P(1)=Q(3)
=>\(a^2+9a+12=a^2-2a+1\)
=>11a=-11
=>a=-1

x+y-3=0
=>x+y=3
\(M\left(x\right)=x^3+x^2y-3x^2-xy-y^2+4y+x+2020\)
\(=x^2\left(x+y\right)-3x^2-y\left(x+y\right)+4y+x+2020\)
\(=3x^2-3x^2-3y+4y+x+2020\)
=x+y+2020
=3+2020
=2023

a) \(P\left(x\right)=x^5-2x^4+3x^2-x+2;Q\left(x\right)=x^4-2x^3+x-5\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)+\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2+x^4-2x^3+x-5\)
\(=x^5+\left(-2x^4+x^4\right)-2x^3+3x^2+\left(-x+x\right)+\left(2-5\right)\)
\(=x^5-x^4-2x^3+3x^2-3\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^5-2x^4+3x^2-x+2\right)-\left(x^4-2x^3+x-5\right)\)
\(=x^5-2x^4+3x^2-x+2-x^4+2x^3-x+5\)
\(=x^5+\left(-2x^4-x^4\right)+2x^3+3x^2+\left(-x-x\right)+\left(2+5\right)\)
\(=x^5-3x^4+2x^3+3x^2-2x+7\)
b) \(P\left(x\right)=x^4+3x^5-x^2-4;Q\left(x\right)=x^4-x^2-3x^3+x\)
+, \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)+\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4+x^4-x^2-3x^3+x\)
\(=3x^5+\left(x^4+x^4\right)-3x^3+\left(-x^2-x^2\right)+x-4\)
\(=3x^5+2x^4-3x^3-2x^2+x-4\)
+, \(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^5-x^2-4\right)-\left(x^4-x^2-3x^3+x\right)\)
\(=x^4+3x^5-x^2-4-x^4+x^2+3x^3-x\)
\(=3x^5+\left(x^4-x^4\right)+3x^3+\left(-x^2+x^2\right)-x-4\)
\(=3x^5+3x^3-x-4\)
\(\text{#}Toru\)

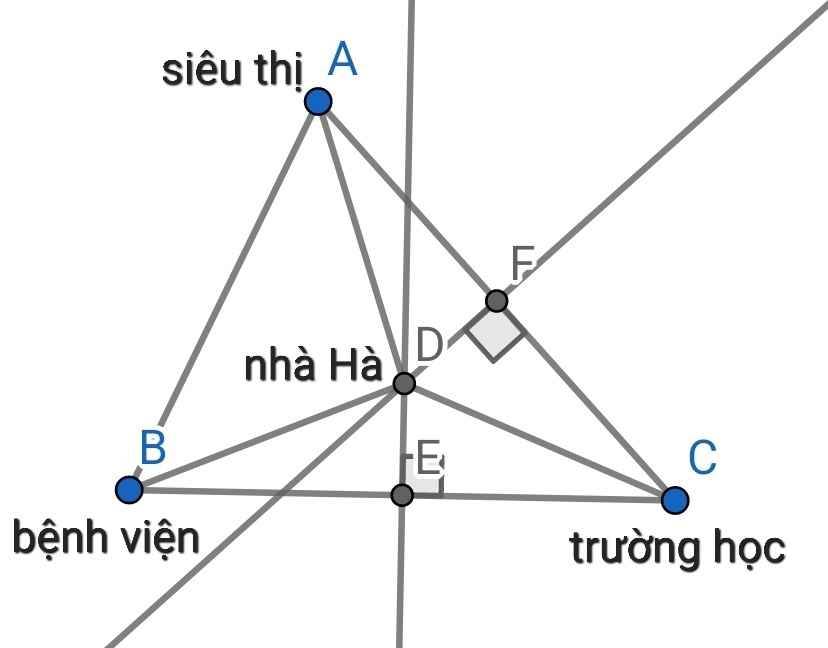
Để khoảng cách từ vị trí của nhà Hà đến siêu thị, bệnh viện, trường học đều bằng nhau thì nhà Hà nằm ở vị trí D là giao điểm của ba đường trung trực của ∆ABC như hình vẽ.
Siêu thị, bệnh viện, trường học nằm ở ba vị trí là ba đỉnh của ∆ABC

Lời giải:
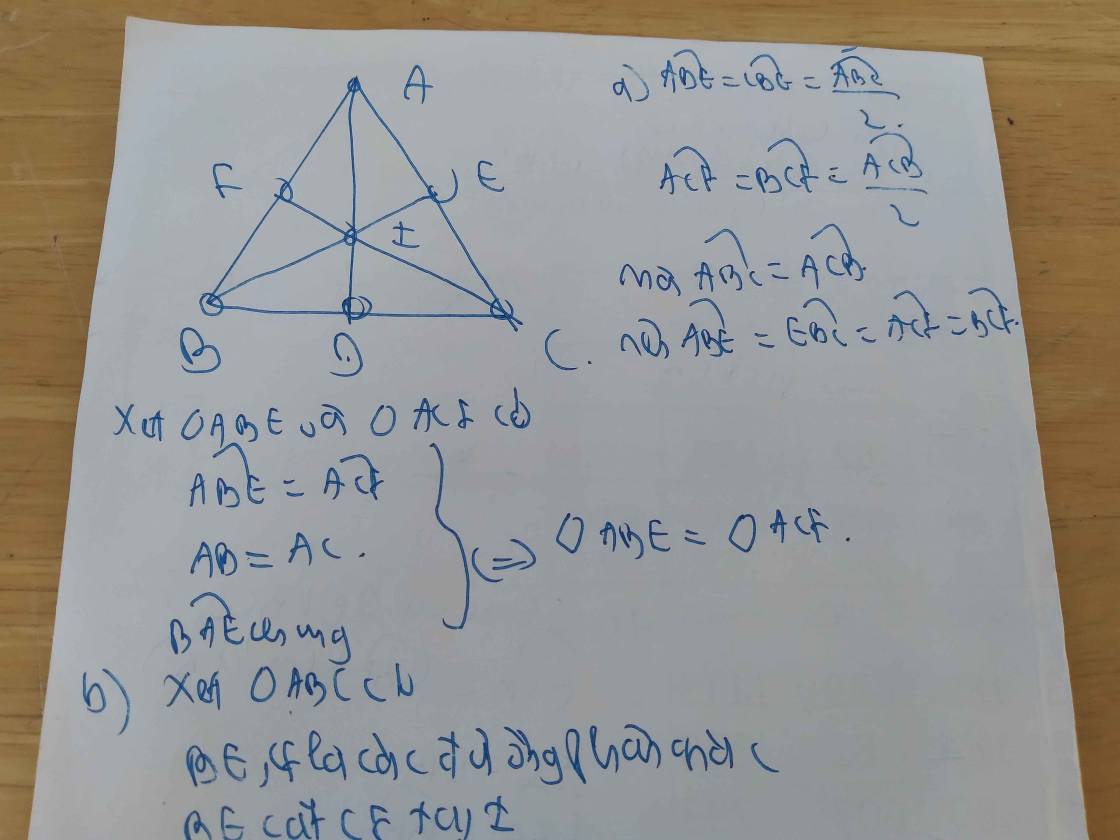
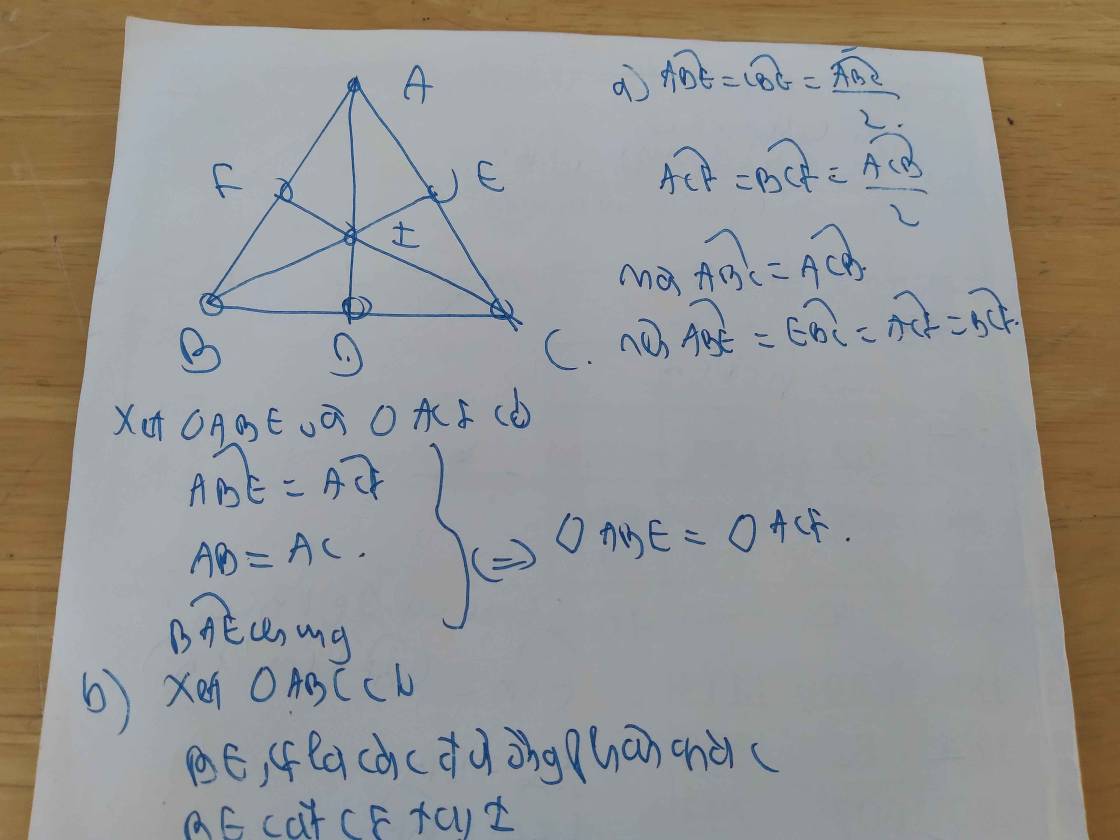
a.
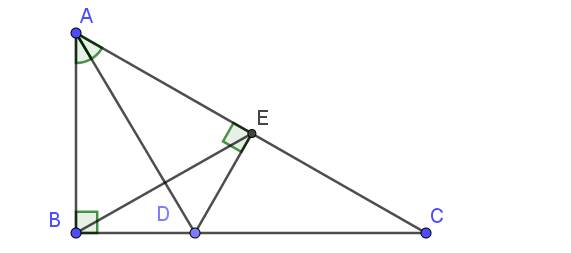
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
b.
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.

Gọi A là biến cố "quả bóng lấy ra là số nguyên tố"
=>A={5}
=>n(A)=1
\(P\left(A\right)=\dfrac{1}{5}\)
Gọi B là biến cố "Quả bóng lấy ra ghi số chia hết cho 5"
=>B={5;10;15;20;25}
=>n(B)=5
\(P\left(B\right)=\dfrac{5}{5}=1\)
Gọi C là biến cố "Quả bóng lấy ra ghi số chia hết cho 6"
=>C=\(\varnothing\)
=>\(P\left(C\right)=0\)
a: Biến cố chắc chắn là biến cố B
b: \(P\left(A\right)=\dfrac{1}{5}\)

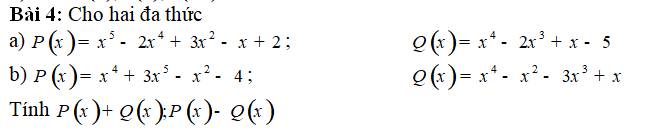





\(x\) < \(x\) là sao em?
2 < x < 20 cô ạ