đặt tính rồi tính:14496:24
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1}{3}+\dfrac{2}{3}+\dfrac{4}{3}+\dfrac{19}{3}=\dfrac{1+2+4+19}{3}=\dfrac{26}{3}\)
\(\dfrac{3}{4}+\dfrac{4}{4}+\dfrac{5}{4}+\dfrac{6}{4}+\dfrac{x}{4}+\dfrac{8}{2}+\dfrac{9}{4}\)
=\(\dfrac{3}{4}+\dfrac{4}{4}+\dfrac{5}{4}+\dfrac{6}{4}+\dfrac{x}{4}+\dfrac{16}{4}+\dfrac{9}{4}\)
=\(\dfrac{3+4+5+6+x+16+9}{4}=\dfrac{43+x}{4}\)
Cảm ơn và chúc Lê Minh Quang học tốt nhé!
Mình đã tick rùi nha
Thanks

EM THAM KHẢO NHÉ !
Sau khi bán đi tổng số gà và vịt còn lại là: (290 - 24 - 35 = 231) (con)
Ta có sơ đồ sau khi bán 24 con gà và 35 con vịt là:

Theo sơ đồ, tổng số phần bằng nhau là: (4 + 7 = 11) (phần)
Số gà còn lại là: (231:11 times 4 = 84) (con)
Số gà ban đầu là: (84 + 24 = 108) (con)
Số vịt ban đầu là: (290 - 108 = 182) (con)
Đáp số: 108 con gà và 182 con vịt.
Em tham khảo nhé
Sau khi bán đi tổng số gà và vịt còn lại là: (290 - 24 - 35 = 231) (con)
Ta có sơ đồ sau khi bán 24 con gà và 35 con vịt là:

Theo sơ đồ, tổng số phần bằng nhau là: (4 + 7 = 11) (phần)
Số gà còn lại là: (231:11 times 4 = 84) (con)
Số gà ban đầu là: (84 + 24 = 108) (con)
Số vịt ban đầu là: (290 - 108 = 182) (con)
Đáp số: 108 con gà và 182 con vịt.

\(a^2+b^2+c^2+d^2+1=a\left(b+c+d+1\right)\)
\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4=4ab+4ac+4ad+4a\)
\(\Leftrightarrow a^2-4ab+4b^2+a^2-4ac+4c^2+a^2-4ad+4d^2+a^2-4a+4=0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2b\\a=2c\\a=2d\\a=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=c=d=1\end{matrix}\right.\).
Vậy \(\left(a,b,c,d\right)=\left(2,1,1,1\right)\)


\(\sqrt{\left(4-3\sqrt{2}\right)^2}=\left|4-3\sqrt{2}\right|=3\sqrt{2}-4\)
\(\sqrt{\left(2+\sqrt{5}\right)^2}=\left|2+\sqrt{5}\right|=2+\sqrt{5}\\ \sqrt{\left(4+\sqrt{2}\right)^2}=\left|4+\sqrt{2}\right|=4+\sqrt{2}\)
\(\sqrt{6-2\sqrt{5}}=\sqrt{\sqrt{5^2}-2\sqrt{5}+1}=\sqrt{\left(\sqrt{5}-1\right)^2}=\left|\sqrt{5}-1\right|=\sqrt{5}-1\\ \sqrt{7+4\sqrt{3}}=\sqrt{\sqrt{3^2}+2.2\sqrt{3}+2^2}=\sqrt{\left(\sqrt{3}+2\right)^2}=\left|\sqrt{3}+2\right|=\sqrt{3}+2\\ \sqrt{12-6\sqrt{3}}=\sqrt{\sqrt{3^2}-2.3\sqrt{3}+3^2}=\sqrt{\left(\sqrt{3}-3\right)^2}=\left|\sqrt{3}-3\right|=3-\sqrt{3}\)
\(\sqrt{17+12\sqrt{2}}=\sqrt{\left(2\sqrt{2}\right)^2+2.2\sqrt{2}.3+3^2}=\sqrt{\left(2\sqrt{2}+3\right)^2}=\left|2\sqrt{2}+3\right|=2\sqrt{2}+3\)
\(\dfrac{\sqrt{2}-\sqrt{11+6\sqrt{2}}}{\sqrt{6+2\sqrt{5}}-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\sqrt{\sqrt{2^2}+2.3\sqrt{2}+3^2}}{\sqrt{\sqrt{5^2}+2\sqrt{5}+1}-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\sqrt{\left(\sqrt{2}+3\right)^2}}{\sqrt{\left(\sqrt{5}+1\right)^2}-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\left|\sqrt{2}+3\right|}{\left|\sqrt{5}+1\right|-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\sqrt{2}-3}{\sqrt{5}+1-\sqrt{5}}\\ =-3\)
\(\sqrt{6+2\sqrt{4-2\sqrt{3}}}=\sqrt{6+2\sqrt{\left(\sqrt{3}-1\right)^2}}=\sqrt{6+2\left|\sqrt{3}-1\right|}=\sqrt{6+2\sqrt{3}-2}=\sqrt{4+2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)

a) \(A=\dfrac{x^4+x}{x^2-x+1}+1-\dfrac{2x^2+x}{x}\)
\(A=\dfrac{x.\left(x^3+1\right)}{x^2-x+1}+1-\dfrac{x.\left(2x+1\right)}{x}\)
\(A=\dfrac{x.\left(x+1\right).\left(x^2-x+1\right)}{x^2-x+1}+1-\left(2x+1\right)\)
\(A=x\left(x+1\right)+1-2x-1\)
\(A=x^2+x-2x=x^2-x\)
b) \(A=6\)
\(\Leftrightarrow x^2-x=6\)
\(\Leftrightarrow x^2-x-6=0\)\(\)
\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow x-3=0\) hay \(x+2=0\)
\(\Leftrightarrow x=3\) hay \(x=-2\)
c) \(A=x^2-x\)
\(A=x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\)
\(A=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\)
mà \(\left(x-\dfrac{1}{2}\right)^2\ge0\)
\(\Rightarrow A=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
\(\Rightarrow Min\left(A\right)=-\dfrac{1}{4}\)

a) \(\dfrac{-12}{17}< \dfrac{x}{17}< \dfrac{-8}{17}\)
\(\Rightarrow-12< x< -8\)
\(\Rightarrow x\in\left\{-11;-10;-9\right\}\)
b) \(\dfrac{-1}{2}< x< \dfrac{5}{3}\)
\(\Rightarrow\dfrac{-3}{6}< x< \dfrac{10}{6}\)
\(\Rightarrow x\in\left\{\dfrac{-2}{6};\dfrac{-1}{6};0;\dfrac{1}{6};...;\dfrac{7}{6};\dfrac{8}{6};\dfrac{9}{6}\right\}\)
c) \(3,456< x\le7,89\)
\(\Rightarrow x\in\left\{3,456;3,457,3,458;...;7,89\right\}\)
d) \(5,82< \overline{5,8x0}< 8,845\)
\(\Rightarrow x\in\left\{3;4\right\}\)
e) \(32,82< \overline{3x,850}< 35,845\)
\(\Rightarrow x\in\left\{3;4\right\}\)

Số tuổi của mẹ là:
\(7\times5=35\) (tuổi)
Mẹ hơn con số tuổi là:
\(35-5=30\) (tuổi)
Do khi tuổi mẹ bằng 4 lần tuổi con thì tuổi mẹ vẫn hơn con 30 tuổi
Ta có sơ đồ:
Tuổi con: |-----|
Tuổi mẹ: |-----|-----|-----|-----|
Hiệu số phần bằng nhau:
\(4-1=3\) (phần)
Khi tuổi mẹ bằng 4 lần tuổi con thì tuổi con là:
\(30:3=10\) (tuổi)
Vậy sau hiện tại số năm là:
\(10-5=5\) (năm)
Đáp số: ...

A B C P Q K H
a/
\(AQ\perp AB;PH\perp AB\) => AQ//PH
\(AP\perp AC;QH\perp AC\) => AP//QH
=> APHQ là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có \(\widehat{A}=90^o\)
=> APHQ là hình chữ nhật (Hình bình hành có 1 góc vuông là HCN)
b/
Xét tg vuông QHC có
KH=KC (gt)
\(\Rightarrow QK=\dfrac{AC}{2}\) (Trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Mà \(KH=KC=\dfrac{HC}{2}\)
=> QK=KH => tg KQH cân tại K

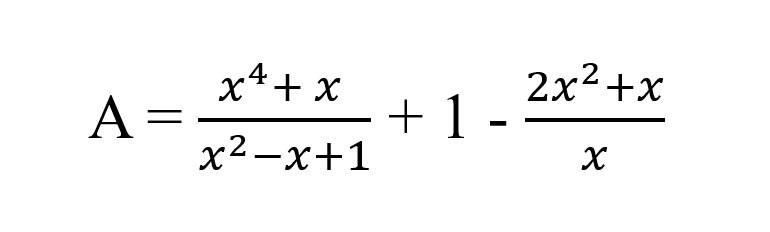
14496 24 64 096 0
\(14496:24=604x24:24=604\)