Số số hạng của phép tính là \(\dfrac{\left(49-1\right)}{2}+1=25\) số hạng

\(K=1x\left(100-1\right)+3x\left(100-3\right)+5x\left(100-5\right)+...+49x\left(100-49\right)=\)

\(=100x\left(1+3+5+...+49\right)-\left(1^2+3^2+5^2+...+49^2\right)=\)

Đặt

\(A=1+3+5+...+49\)

\(B=1^2+3^2+5^2+...+49^2\)

\(B=1x\left(3-2\right)+3x\left(5-2\right)+5\left(7-2\right)+...+49x\left(51-2\right)=\)

\(1x3+3x5+5x7+...+49x51-2\left(1+3+5+...+49\right)=\)

\(K=100xA-B=102xA-\left(1x3+3x5+5x7+...+49x51\right)=\)

A là cấp số cộng có 25 số hạng; d=2

Đặt

 \(C=1x3+3x5+5x7+...+49x51\)

\(6xC=1x3x\left(5+1\right)+3x5x\left(7-1\right)+5x7x\left(9-3\right)+...+49x51x\left(53-47\right)=\)

\(=1.3+1.3.5-1.3.5+3.5.7-3.5.7+5.7.9+...-47.49.51+49.51.53=\)

\(=1.3+49x51x53\Rightarrow C=\dfrac{1.3+49.51.53}{6}\)

Bạn tự tính toán nốt nhé

\(\dfrac{11}{3}:\dfrac{x}{5}=\dfrac{5}{9}\)
\(\dfrac{x}{5}=\dfrac{11}{3}:\dfrac{5}{9}\)
\(\dfrac{x}{5}=\dfrac{33}{5}\)
\(x=33\)

Good Job nha

  36 + 48 + 40 + 42 + 44 + 46 + 48 + 50

= (36 + 48) + (40 + 50) + (42 + 48) + (44 +46)

= 84 + 90 + 90 + 90 

= 74 + 90 \(\times\) 3

= 74 + 270

= 344

36 + 38 + 40 + 42 + 44 + 46 + 48 + 50

= (36 + 50){ (50-36):2+1}: 2

= 344

Tổng vận tốc hai xe là: 50 + 45 = 95 (km/h)

Thời gian hai xe gặp nhau là: 142,5 : 95 = 1,5 (giờ)

Đổi 1,5 giờ = 1 giờ 30 phút

Hai xe gặp nhau lúc: 

6 giờ 40 phút + 1 giờ 30 phút = 8 giờ 10 phút

Đáp số: 8 giờ 10 phút 

(2²)³ và 2⁶

(2²)³ = 2^2.3 = 2⁶

Vậy (2²)³ = 2⁶

\(\left(2^2\right)^3\) và \(2^6\)

- \(\left(2^2\right)^3=64\)

- \(2^6=64\)

Vì \(64=64\)

Nên \(\left(2^2\right)^3=2^6\)

 TH1: Nếu \(a\ge b\ge c\) thì đk đã cho tương đương với \(3\left(a-b\right)=5\left(b-c\right)=7\left(a-c\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}3a-3b=5b-5c\\5b-5c=7a-7c\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a+5c=8b\\7a-2c=5b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6a+10c=16b\\35a-10c=25b\end{matrix}\right.\) \(\Rightarrow41a=41b\Leftrightarrow a=b\). Điều này có nghĩa là \(a-b=0\), từ đó suy ra \(5\left(b-c\right)=0\Leftrightarrow b=c\). Vậy \(a=b=c\).

 TH2: Nếu \(b\ge c\ge a\) thì đk đã cho tương đương với \(3\left(b-a\right)=5\left(b-c\right)=7\left(c-a\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}3b-3a=5b-5c\\5b-5c=7c-7a\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a+2b=5c\\7a+5b=12c\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}15a+10b=25c\\-14a-10b=-24c\end{matrix}\right.\) \(\Rightarrow a=c\). Từ đó suy ra \(a-c=0\) hay \(3\left(b-a\right)=0\Leftrightarrow a=b\). Vậy \(a=b=c\).

 TH3: Nếu \(c\ge a\ge b\) thì đk đã cho tương đương với \(3\left(a-b\right)=5\left(c-b\right)=7\left(c-a\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}3a-3b=5c-5b\\5c-5b=7c-7a\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a+2b=5c\\7a-5b=2c\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}15a+10b=25c\\14a-10b=4c\end{matrix}\right.\) \(\Rightarrow29a=29c\Leftrightarrow a=c\). Từ đó suy ra \(a-c=0\) hay \(3\left(a-b\right)=0\Leftrightarrow a=b\). Vậy \(a=b=c\)

 Tất cả các trường hợp còn lại làm tương tự và đều suy ra được \(a=b=c\). Ta có đpcm.

hi =D

Gọi UWCNL(2n+3,2n+2) là d ( d khác 0 )

=> \(2n+3⋮d;2n+2⋮d\) 

=> \(\left(2n+3\right)-\left(2n+2\right)⋮d\) 

=> \(1⋮d\) 

=> \(d=1\) 

     Vậy 2n+3 và 2n+2 là 2 số nguyên tố cùng nhau

Giả sử trong 2021 số tự nhiên tồn tại ít nhất một số chẵn ta có:

chẵn + lẻ + lẻ + lẻ + lẻ = chẵn (vô lý)

Vì tổng của năm số tự nhiên bất kỳ trong 2021 số tự nhiên phải là số lẻ

Như vậy trong 2021 số tự nhiên thỏa mãn đề bài thì không tồn tại bất cứ số nào là số chẵn, hay tất cả 2021 số tự nhiên đó đều là số lẻ.

Khi đó tổng 5 số tự nhiên bất kỳ trong 2021 số tự nhiên là số:  

lẻ + lẻ + lẻ + lẻ + lẻ = lẻ (thỏa mãn)

Mặt khác ta có:

2021 : 5 =  404 dư 1

Nên tổng của 2021 số tự nhiên sẽ là tổng của: 

404 nhóm và 1 số tự nhiên lẻ mà mỗi nhóm là một số lẻ nên 

A = lẻ + lẻ + lẻ + ...+ lẻ ( 405 số lẻ)

A là số lẻ 

\(\left(9x-21\right)\div3=2\) 

         \(9x-21=2\times3\) 

          \(9x-21=6\) 

                 \(9x=6+21\) 

                 \(9x=27\) 

                   \(x=27\div9\) 

                    \(x=3\)

(9\(x\) - 21): 3 =2

9\(x\) - 21 = 2.3

9\(x-21=6\)

9\(x\)          = 6 + 21

9\(x\)          = 27

  \(x\)          = 27: 9

  \(x\)           = 3

Bình có số vở là: 20 \(\times\) \(\dfrac{1}{2}\) = 10 (quyển)

Tổng số vở của Bình và An là: 20 + 10 = 30 (quyển)

Ta có sơ đồ:

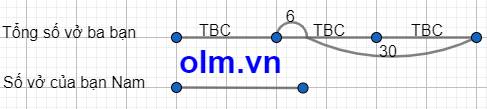
Theo sơ đồ ta có:

Trung bình cộng số vở ba bạn là: (30 + 6) : 2 = 18 (quyển)

Số vở của Nam là: 18 + 6 = 24 (quyển)

Đáp số: 24 quyển