\(\frac{x-1}{2}=\frac{y+3}{4}=\frac{z-5}{6}\) và 5z-3x-4y=50
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Tổng số viên bi là: 5 + 5 = 10 (viên bi)
Xác xuất của biến cố lấy được viên bi màu đỏ là:
5 : 10 = \(\frac12\)
Xác xuất của biến cố lấy được viên bi màu xanh là:
5 : 10 = \(\frac12\)
Kết luận:
a; Xác xuất của biến cố lấy được viên bi màu đỏ là: \(\frac12\)
b; Xác xuất của biến cố lấy được viên bi mà xanh là: \(\frac12\)
a: Số cách bốc 1 viên bi bất kì trong hộp là:
5+5=10(cách)
Xác suất bốc được viên bi đỏ là \(\dfrac{5}{10}=\dfrac{1}{2}\)
b: Xác suất bốc được viên bi xanh là \(\dfrac{5}{10}=\dfrac{1}{2}\)

Thể tích của bể là:
50 x 20 x 40 = 40 000 ( cm3 )
Sau khi lấy đi 3600 cm3 thì thể tích nước còn lại trong bể là:
40 000 - 3 600 = 36 400 ( cm3 )
Mực nước trong bể sau khi lấy đi 3600 cm3 là:
36 400 : ( 50 x 20 ) = 36,4 ( cm )
a) Thể tích bể:
50.20.40 = 40000 (cm³)
b) Thể tích nước còn lại trong bể:
40000 - 3600 = 36400 (cm³)
Chiều cao mực nước còn lại trong bể:
36400 : 50 : 20 = 36,4 (cm)

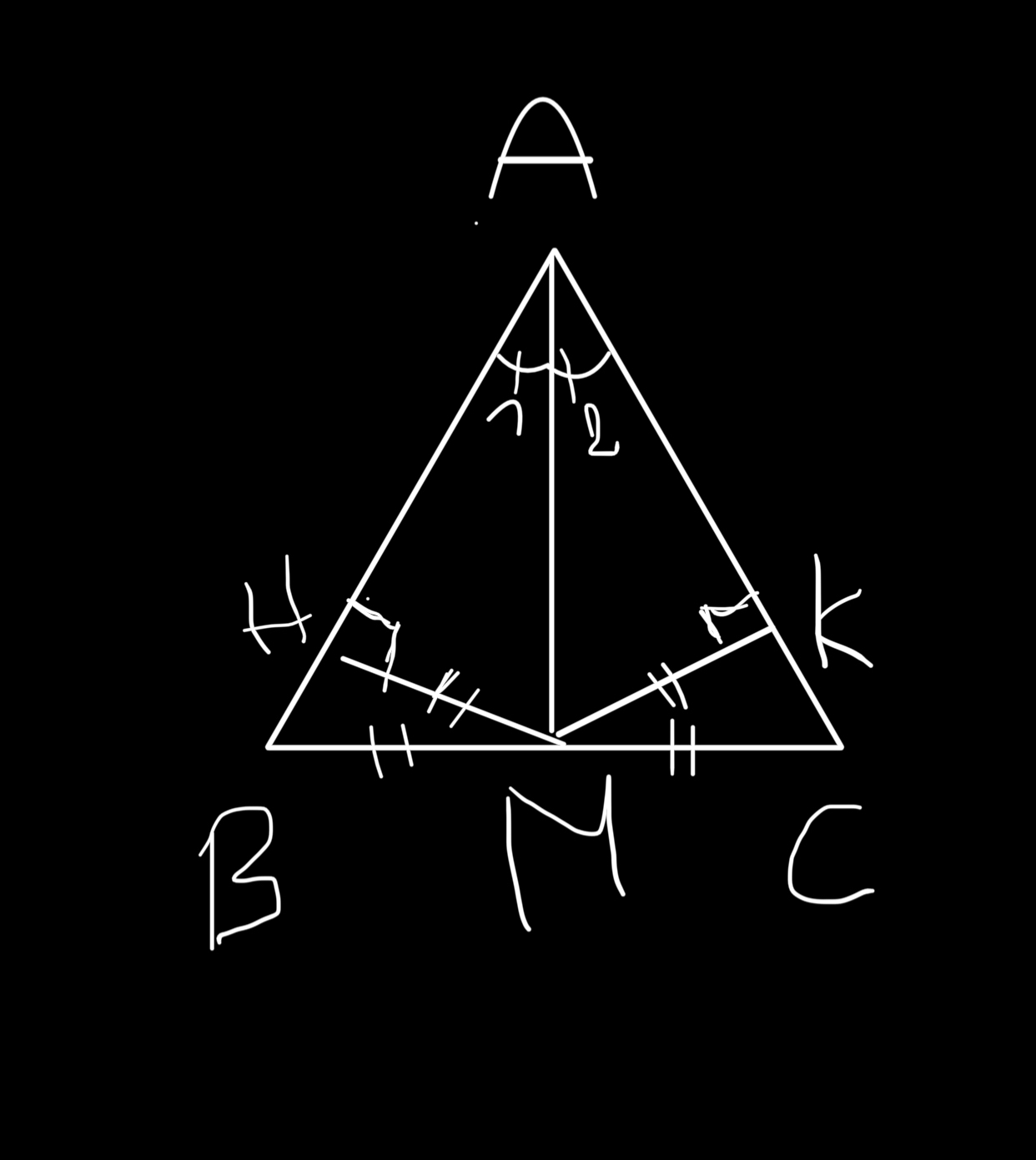
Ký hiệu vậy chưa được em. Vì em ký hiệu vậy nghĩa là BM = CM = HM = KM
Trong khi chỉ có BM = CM; HM = KM

5x/7 = 10/-3
=> 5x.(-3) = 7.10
5x.(-3) = 70
5x = 70/-3
x = -70/3 : 5
x = -14/3
Vậy x = -14/3
#ngophuongloan(chipcuti)
Chúc bạn học tốt hjhj!!
Vì \(\frac{5x}{7}=\frac{10}{-3}\) là một tỉ lệ thức
\(\Rightarrow5x.\left(-3\right)=7.10\)
\(5x.\left(-3\right)=70\)
\(5x=70:\left(-3\right)\)
\(5x=\frac{-70}{3}\)
\(x=\left(-\frac{70}{3}\right):5\)
\(x=-\frac{14}{13}\)
Vậy \(x=-\frac{14}{13}\)

Diện tích mảnh vườn hình chữ nhật là : 35 . 28 = 980 (\(m^2\))
Số ki-lô-gam cà chua thu hoạch được trên cả mảnh vườn là :
980 : 4 . 3 = 735 (kg)
Đ/s : 735 kg
giải
Diện tích mảnh vườn hình chữ nhật là:
35 . 28 =980 (m2)
Tổng số kg cà chua thu hoạch được trên mảnh vườn là:
980:4= 254 (kg)
sai cho tớ xl ạ

\(\dfrac{x}{4}=\dfrac{x\cdot2}{4\cdot2}=\dfrac{2x}{8}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{12}{3}=4\\ \dfrac{2x}{8}=4\Rightarrow x=16\\ \dfrac{y}{5}=4\Rightarrow y=20\)
vậy x = 16; y = 20
có x/4=y/5 suy ra 2x/8= y/5
áp dụng t/c của dãy tỉ số bằng nhau ta có
2x/8=y/5=2x-y/8-5=4
suy ra
2x/8=4 y/5=4
x=16 y=20

Giải:
Gọi số vở của ba lớp 7A; 7B; 7C lần lượt là: \(x;y;z\) (\(x;y;z\in N\) *)
Theo bài ra ta có: \(\frac{x}{10}\) = \(\frac{y}{14}\) = \(\frac{z}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{10}\) = \(\frac{y}{14}=\frac{z}{13}\) = \(\frac{z-x}{13-10}\) = \(\frac{30}{3}\) = 10
\(x\) = 10 x 10 = 100(quyển)
y = 10 x 14 = 140 (quyển)
z = 10 x 13 = 130 (quyển)
Kết luận số vở lớp 7A; 7B; 7C góp được lần lượt là:
100; 130; 140 quyển
Đặt \(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=k\)
=>\(\left\{{}\begin{matrix}x-1=2k\\y+3=4k\\z-5=6k\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2k+1\\y=4k-3\\z=6k+5\end{matrix}\right.\)
-3x-4y+5z=50
=>-3(2k+1)-4(4k-3)+5(6k+5)=50
=>\(-6k-3-16k+12+30k+25=50\)
=>8k+34=50
=>8k=16
=>k=2
=>\(\left\{{}\begin{matrix}x=2\cdot2+1=5\\y=4\cdot2-3=8-3=5\\z=6\cdot2+5=12+5=17\end{matrix}\right.\)