để xây dựng phương án kinh doanh cho 1 loại sản phẩm , doanh nghiệp tính toán lợi nhuận y ( đồng ) theo công thức sau : y= -86x^2+86000x-18146000 , trong đó x là số sản phâ,r được bán ra . hỏi doanh nghiệp sẽ bị lỗ khi bán tối đa hay tối thiểu bao nhiêu sản phẩm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(x=\dfrac{7}{25}+\dfrac{-1}{5}\)
\(\Rightarrow x=\dfrac{7}{25}+\dfrac{-5}{25}\)
\(\Rightarrow x=\dfrac{2}{25}\)c
b) \(x=\dfrac{5}{11}+\dfrac{4}{-9}\)
\(\Rightarrow x=\dfrac{45}{99}+\dfrac{-44}{99}\)
\(\Rightarrow x=\dfrac{1}{99}\)
c) \(x-\dfrac{5}{7}=\dfrac{1}{9}\)
\(\Rightarrow x=\dfrac{1}{9}+\dfrac{5}{7}\)
\(\Rightarrow x=\dfrac{7}{63}+\dfrac{45}{63}\)
\(\Rightarrow x=\dfrac{52}{63}\)
d) \(x-\dfrac{5}{7}=\dfrac{2}{7}\cdot\dfrac{11}{5}\)
\(\Rightarrow x-\dfrac{5}{7}=\dfrac{22}{35}\)
\(\Rightarrow x=\dfrac{22}{35}+\dfrac{5}{7}\)
\(\Rightarrow x=\dfrac{22}{35}+\dfrac{25}{35}\)
\(\Rightarrow x=\dfrac{47}{35}\)
e) \(\dfrac{3}{4}-x=1\)
\(\Rightarrow x=\dfrac{3}{4}-1\)
\(\Rightarrow x=-\dfrac{1}{4}\)
f) x + 4 = 1/5
x = 1/5 - 4
x = 1/5 - 20/5
x = -19/5
g) x - 1/5 = 2
x = 2 + 1/5
x = 10/5 + 1/5
x = 11/5
h) x + 5/3 = 1/27
x = 1/27 - 5/3
x = 1/27 - 45/27
x = -44/27
i) x/15 = 3/5 + (-2/3)
x/15 = 9/15 - 10/15
x/15 = -1/15
x = -1
k) 3x/4 = 18/(3x + 1)
3x(3x + 1) = 18.4 (1)
Đặt t = 3x
(1) ⇒ t(t + 1) = 72
t² + t - 72 = 0
t² - 8t + 9t - 72 = 0
(t² - 8t) + (9t - 72) = 0
t(t - 8) + 9(t - 8) = 0
(t - 8)(t + 9) = 0
t - 8 = 0 hoặc t + 9 = 0
*) t - 8 = 0
t = 8
3x = 8
x = 8/3
*) t + 9 = 0
t = -9
3x = -9
x = -9 : 3
x = -3
Vậy x = -3; x = 8/3

a; \(x\) = \(\dfrac{7}{25}\) + \(\dfrac{-1}{5}\)
\(x\) = \(\dfrac{7}{25}\) - \(\dfrac{5}{25}\)
\(x=\dfrac{2}{25}\)
b; \(x=\dfrac{5}{11}\) + \(\dfrac{4}{-9}\)
\(x=\dfrac{45}{99}-\dfrac{44}{99}\)
\(x=\dfrac{1}{99}\)
c; \(x\) - \(\dfrac{5}{7}\) = \(\dfrac{1}{9}\)
\(x\) = \(\dfrac{1}{9}\) + \(\dfrac{5}{7}\)
\(x=\dfrac{7}{63}+\dfrac{45}{63}\)
\(x\) = \(\dfrac{52}{63}\)

bài 2 : bài giải
32 công nhân trong 1 giờ chuyển được số hàng hóa là :
30:2=15(tạ)
1 công nhân trong 1 giờ chuyển được số hàng hóa là :
15:32=0.46875(tạ)
12 công nhân trong 1 giờ chuyển được số hàng hóa là :
0.46875 x 12 = 5.625(tạ)
12 công nhân trong 4 giờ chuyển được số hàng hóa là :
5.625 x 4 = 22.5 ( tạ )
đáp số : 22.5 tạ hàng hóa
bài 2 : bài giải
32 công nhân trong 1 giờ chuyển được số hàng hóa là :
30:2=15(tạ)
1 công nhân trong 1 giờ chuyển được số hàng hóa là :
15:32=0.46875(tạ)
12 công nhân trong 1 giờ chuyển được số hàng hóa là :
0.46875 x 12 = 5.625(tạ)
12 công nhân trong 4 giờ chuyển được số hàng hóa là :
5.625 x 4 = 22.5 ( tạ )
đáp số : 22.5 tạ hàng hóa

a; \(\dfrac{x}{7}\) = \(\dfrac{9}{y}\) (\(x>y\))
\(x.y\) = 7.9
\(xy\) = 63
Ư(63) = {-63;-21 -9; 7; -3; -1; 1; 3; 7; 9;21; 63}
Lập bảng ta có:
| \(x\) | -63 | -21 | -9 | -7 | -3 | -1 | 1 | 3 | 7 | 9 | 21 | 63 |
| y | -1 | -3 | -7 | -9 | -21 | -63 | 63 | 21 | 9 | 7 | 3 | 1 |
Vì \(x>y\) nên theo bảng trên ta có các cặp số nguyên \(x;y\) thỏa mãn đề bài là:
(\(x;y\)) = (-7; -9); (-3; -21); (-1; -63); (9; 7); (21; 3); (63; 1)
b; \(\dfrac{x}{15}\) = \(\dfrac{3}{y}\) Và \(x< y< 0\)
\(x.y\) = 3.15
\(xy\) = 45
45 = 32.5; Ư(45) = {-45; -15; -9; -5; -3; -1; 1; 3; 5; 9; 15; 45}
Lập bảng ta có:
| \(x\) | -45 | -15 | -9 | -5 | -3 | -1 | 1 | 3 | 5 | 9 | 15 | 45 |
| 4y | -1 | -3 | -5 | -9 | -15 | -45 | 45 | 15 | 9 | 5 | 3 | 1 |
Vì \(x< y< 0\)
Theo bảng trên ta có:
các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(-45; -1); (-15; -3); (-9; -5)

Bài 3.17
a = \(\dfrac{n+8}{2n-5}\) (n \(\in\) N*)
a \(\in\) Z ⇔ n + 8 ⋮ 2n - 5
2.(n + 8) ⋮ 2n - 5
2n + 16 ⋮ 2n - 5
2n - 5 + 21 ⋮ 2n - 5
21 ⋮ 2n - 5
2n - 5 \(\in\) Ư(21)
21 = 3.7; Ư(21) = {-21; -7; -3; -1; 1; 3; 7; 21}
Lập bảng ta có:
| 2n - 5 | -21 | -7 | -3 | -1 | 1 | 3 | 7 | 21 |
| n | -8 (loại) | -1(loại) | -1(loại) | -2(loại) | 3 | 4 | 6 | 13 |
| a =\(\dfrac{n+8}{2n-5}\) | 11(loại) | 4(loại) | 2 | 1(loại) |
Theo bảng trên ta có: n = 6
Vậy n = 6 thì a là số nguyên tố.
\(\dfrac{7n-1}{4}\) \(\in\) N ; \(\dfrac{5n+3}{12}\) \(\in\) N
⇔ \(\left\{{}\begin{matrix}7n-1⋮4\\5n+3⋮12\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}3.\left(7n-1\right)⋮12\\5n+3⋮12\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}21n-3⋮12\\5n+3⋮12\end{matrix}\right.\)
⇒ 21n - 3 + 5n + 3 ⋮ 12
(21n + 5n) ⋮ 12
26n ⋮ 12
13n ⋮ 6
n ⋮ 6
⇒ 7n là số chẵn ⇒ 7n - 1 là số lẻ nên 7n - 1 không chia hết cho 4
Vậy không tồn tại số tự nhiên n nào thỏa mãn đề bài.

Bạn xem lại đề + số liệu. Với số liệu của phép tính trên không thể tính nhanh, nhưng mình vẫn tính cho bạn, bạn nhé!
\(18,7\times3,7+5,7\times18,7-8,7\times4,8-4,6\times7,8\)
\(=18,7\times\left(4,7+5,7\right)-41,76-35,88\)
\(=18,7\times9,4-41,76-35,88\)
\(=175,78-41,76-35,88\)
\(=134,02-35,88\)
\(=98,14\)
cái này không phải đề sai đâu bn đây là đề cô giao cho mình mà

\(S=\dfrac{1}{1!}+\dfrac{1}{2!}+....+\dfrac{1}{2001!}\)
\(S=1+\dfrac{1}{2!}+\dfrac{1}{3!}+.....+\dfrac{1}{2001!}\)
\(\dfrac{1}{2!}=\dfrac{1}{1\times2};\dfrac{1}{3!}< \dfrac{1}{2\times3};...;\dfrac{1}{2001!}< \dfrac{1}{2000\times2001}\)
\(\dfrac{1}{2!}+\dfrac{1}{3!}+....+\dfrac{1}{2001!}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+....+\dfrac{1}{2000\times2001}\)
\(S< 1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2000}-\dfrac{1}{2001}\)
\(S< 2-\dfrac{1}{2001}< 2< 3\)
=> \(S< 3\)

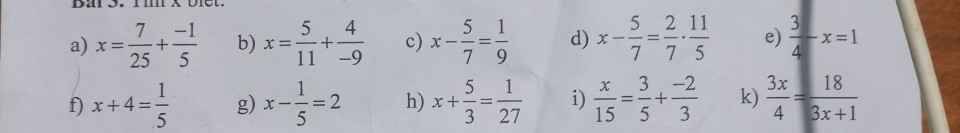
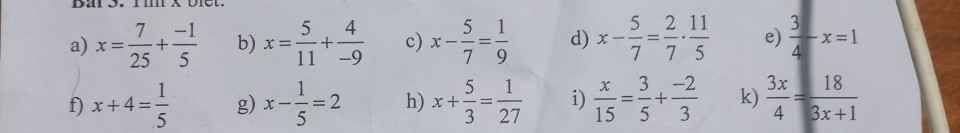

Ta có lợi nhuận được tính theo CT: \(y=-86x^2+86000x-1814600\)
Để biết được doanh nghiệp lỗ khi bán tối đa hay tối thiểu bao nhiêu sản phẩm thì ta cần xét dấu tam thức bậc 2:
\(\Delta=b^2-4ac=86000^2-4\cdot-86\cdot-18146000=1153776000>0\)
Tam thức đã cho có 2 nghiệm:
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-86000+\sqrt{115377600}}{2\cdot-86}=500-10\sqrt{390}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-86000-\sqrt{1153776000}}{2\cdot-86}=500+10\sqrt{390}\)
Khi đó:
\(y< 0\) với mọi x thuộc khoảng \(\left(-\infty;500-10\sqrt{390}\right)\) và \(\left(500+10\sqrt{390};+\infty\right)\)
\(y>0\) với mọi x thuộc khoảng \(\left(500-10\sqrt{390};500+10\sqrt{390}\right)\)
Vậy doanh nghiệp sẽ bị lỗ khi bán ít hơn 302 sản phẩm hoặc nhiều hơn 698 sản phẩm