
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔMAB=ΔMCD
b: Xét ΔCBD có
CM,DN là các đường trung tuyến
CM cắt DN tại G
Do đó: G là trọng tâm của ΔCBD
c: Bạn ghi lại đề đi bạn

Cho tam giác ABC vuông tại A (AB < AC). Vẽ đường trung tuyến BM. Trên tia đối của tia MB, lấy điểm D sao cho M là trung điểm của BD,
a) Chứng minh: tam giác ABM = tam giác CDM.
b) Gọi N là trung điểm của BC, DN cắt AC tại G. Chứng minh: G là trọng tâm của tam giác BCD.
c) CMR: BM-BND < 1/2 BA

Để chứng minh các phát biểu đã cho:
a) Ta có:
\[IM = \frac{AM}{\sqrt{2}}\]
\[= \frac{AP + PM}{\sqrt{2}} - \frac{AQ + MQ}{\sqrt{2}}\]
\[= \frac{AP}{\sqrt{2}} - \frac{AQ}{\sqrt{2}}\]
\[= \frac{PM - MQ}{\sqrt{2}}\]
\[= \frac{PM - MQ}{2}\]
Vậy, a) được chứng minh.
b) Góc CMQ là góc giữa đường thẳng MQ và phân giác của góc A, vì vậy góc CMQ chính bằng một nửa của sự chênh lệch giữa các góc \(ABC\) và \(C\).
\[ \angle CMQ = \frac{1}{2} (\angle ABC - \angle C) \]
c) Để chứng minh \(BP = QC\), chúng ta sẽ sử dụng định lý Phân Tỉ của đường thẳng song song, nghĩa là \(BP/CQ = BM/CM = 1/1\), từ đó suy ra \(BP = QC\).
Vậy, c) cũng được chứng minh.
Do đó, lời giải là:
a) \(IM = \frac{PM - MQ}{2}\)
b) \(Góc CMQ = \frac{(^ABC-^C)}{2}\)
c) \(BP = QC\) tui ko chắc

a: \(M\left(x\right)=3x^4-5x^2-2x^3-4x+6x^2+8x^3-2\)
\(=3x^4+\left(-2x^3+8x^3\right)+\left(6x^2-5x^2\right)-4x-2\)
\(=3x^4+6x^3+x^2-4x-2\)
\(N\left(x\right)=\sqrt{2}x^4+\dfrac{1}{2}x^2-3x^3-\sqrt{2}x^4+5x^3-\dfrac{3}{2}x^2-4x-3\)
\(=\left(\sqrt{2}x^4-\sqrt{2}x^4\right)+\left(-3x^3+5x^3\right)+\left(\dfrac{1}{2}x^2-\dfrac{3}{2}x^2\right)-4x-3\)
\(=2x^3-x^2-4x-3\)
b: G(x)=M(x)+N(x)
\(=3x^4+6x^3+x^2-4x-2+2x^4-x^2-4x-3\)
\(=5x^4+6x^3-8x-5\)
c: H(x)=M(x)-N(x)
\(=3x^4+6x^3+x^2-4x-2-2x^4+x^2+4x+3\)
\(=x^4+6x^3+2x^2+1\)

\(-x^2\left(x^2-4x+3\right)+x\left(x^2+x-3\right)\)
\(=-x^4+4x^3-3x^2+x^3+x^2-3x\)
\(=-x^4+5x^3-2x^2-3x\)

A=(x-5)(x+7)-7x(x+3)
\(=x^2+7x-5x-35-7x^2-21x\)
\(=-6x^2-19x-35\)
(x - 5)(x + 7) - 7x(x + 3)
= x² + 7x - 5x - 35 - 7x² - 21x
= (x² - 7x²) + (7x - 5x - 21x) - 35
= -6x² - 19x - 35

\(P\left(x\right)=-2x^2+3x^4+x^3+x^2-\dfrac{1}{4}x\)
\(=3x^4+x^3+\left(-2x^2+x^2\right)-\dfrac{1}{4}x\)
\(=3x^4+x^3-x^2-\dfrac{1}{4}x\)
Khi x=-1 thì \(P\left(-1\right)=3\cdot\left(-1\right)^4+\left(-1\right)^3-\left(-1\right)^2-\dfrac{1}{4}\cdot\left(-1\right)\)
=3-1-1+1/4
=3+1/4
=3,25


a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔNMI=ΔNKI
b: ta có: ΔNMI=ΔNKI
=>IM=IK
mà IK<IP(ΔIKP vuông tại K)
nên IM<IP
c: Xét ΔIMQ vuông tại M và ΔIKP vuông tại K có
IM=IK
\(\widehat{MIQ}=\widehat{KIP}\)(hai góc đối đỉnh)
Do đó: ΔIMQ=ΔIKP
=>IQ=IP
=>ΔIQP cân tại I
Xét ΔNQP có
QK,PM là các đường cao
QK cắt PM tại I
Do đó: I là trực tâm của ΔNQP
=>NI\(\perp\)PQ tại D
=>ND\(\perp\)PQ
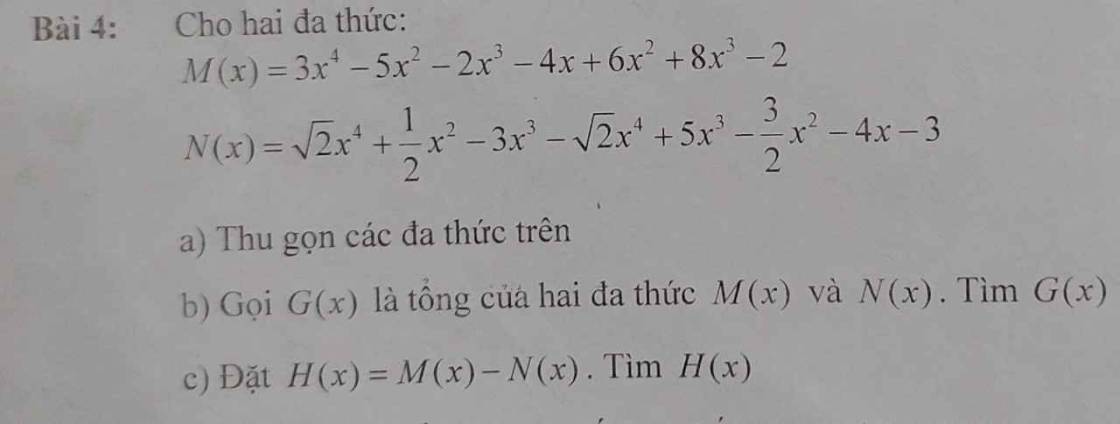

Bài 1b;
\(x^2\) - a\(x\) + 3 ⋮ \(x\) - 3
Theo bezout ta có: \(x^2\) - a\(x\) + 3 ⋮ \(x\) - 3
⇔32 - a.3 + 3 = 0
\ 9 - 3a + 3 = 0
12 - 3a = 0
3a = 12
a = 12 : 3
a = 4
Vậy \(x^2\) - a\(x\) + 3 \(⋮\) \(x\) - 3 khi a = 4
Bạn cần giải bài nào nhỉ? Nếu cần tất cả thì bạn tách câu ra nhé.