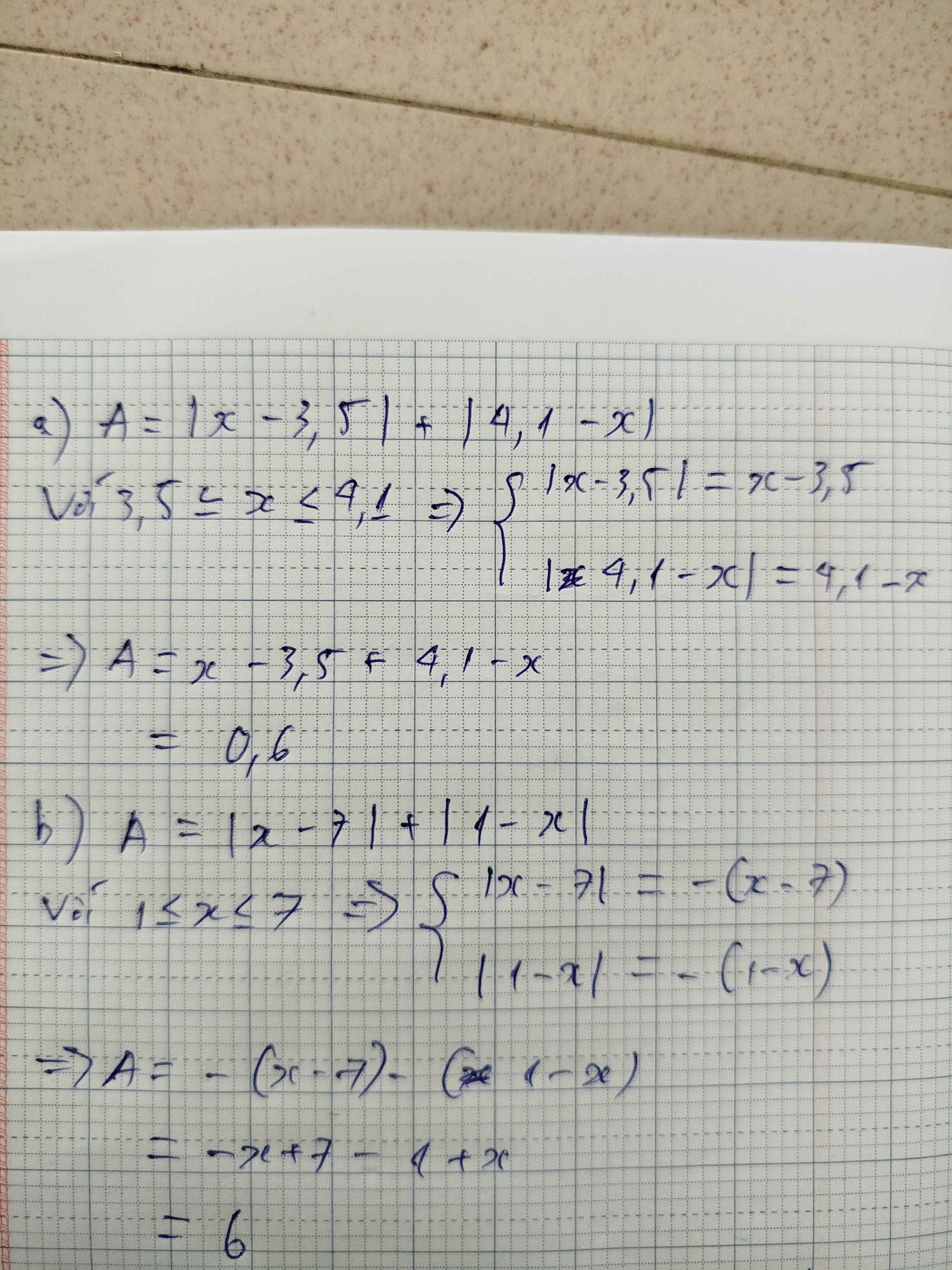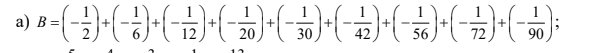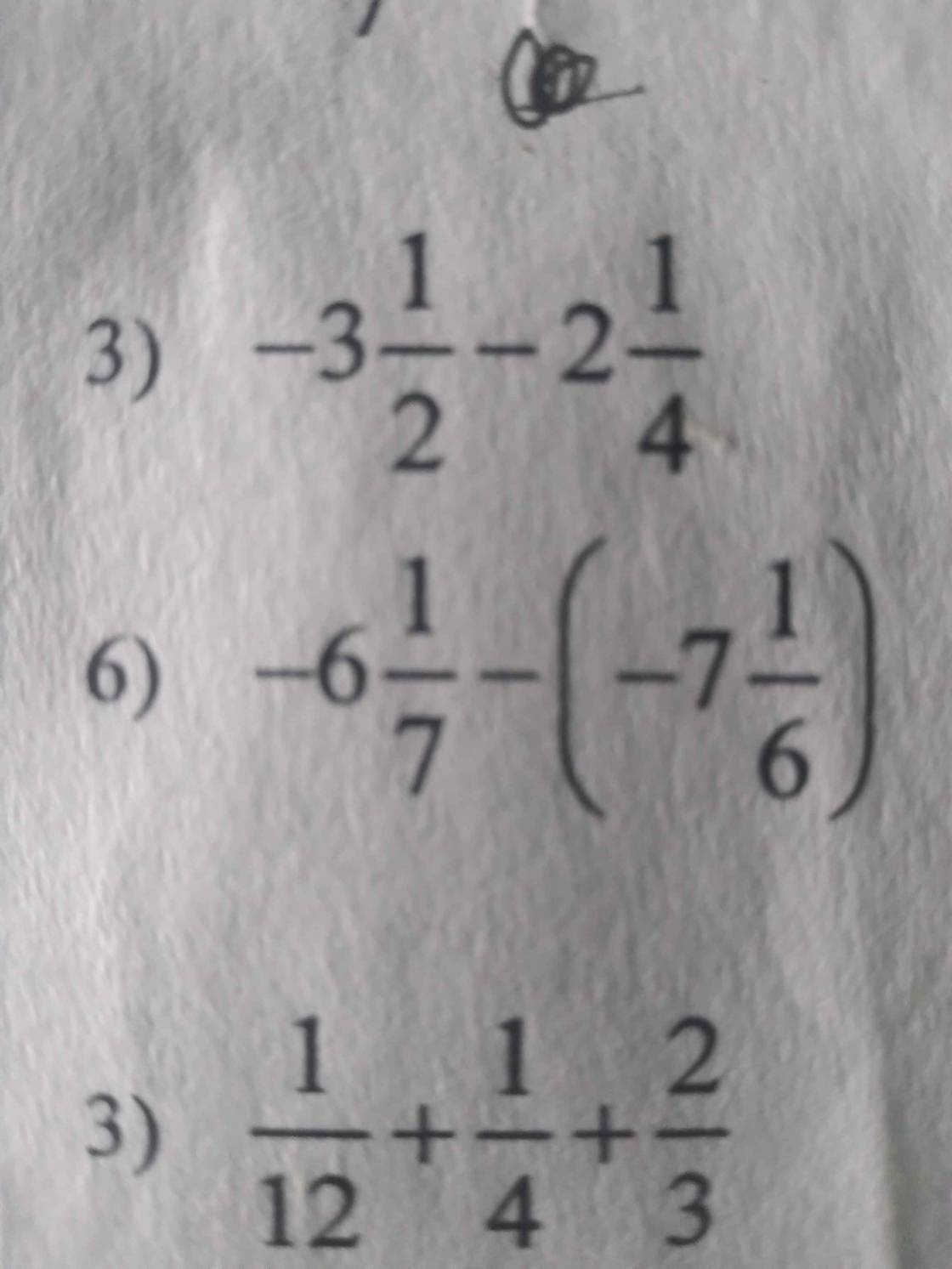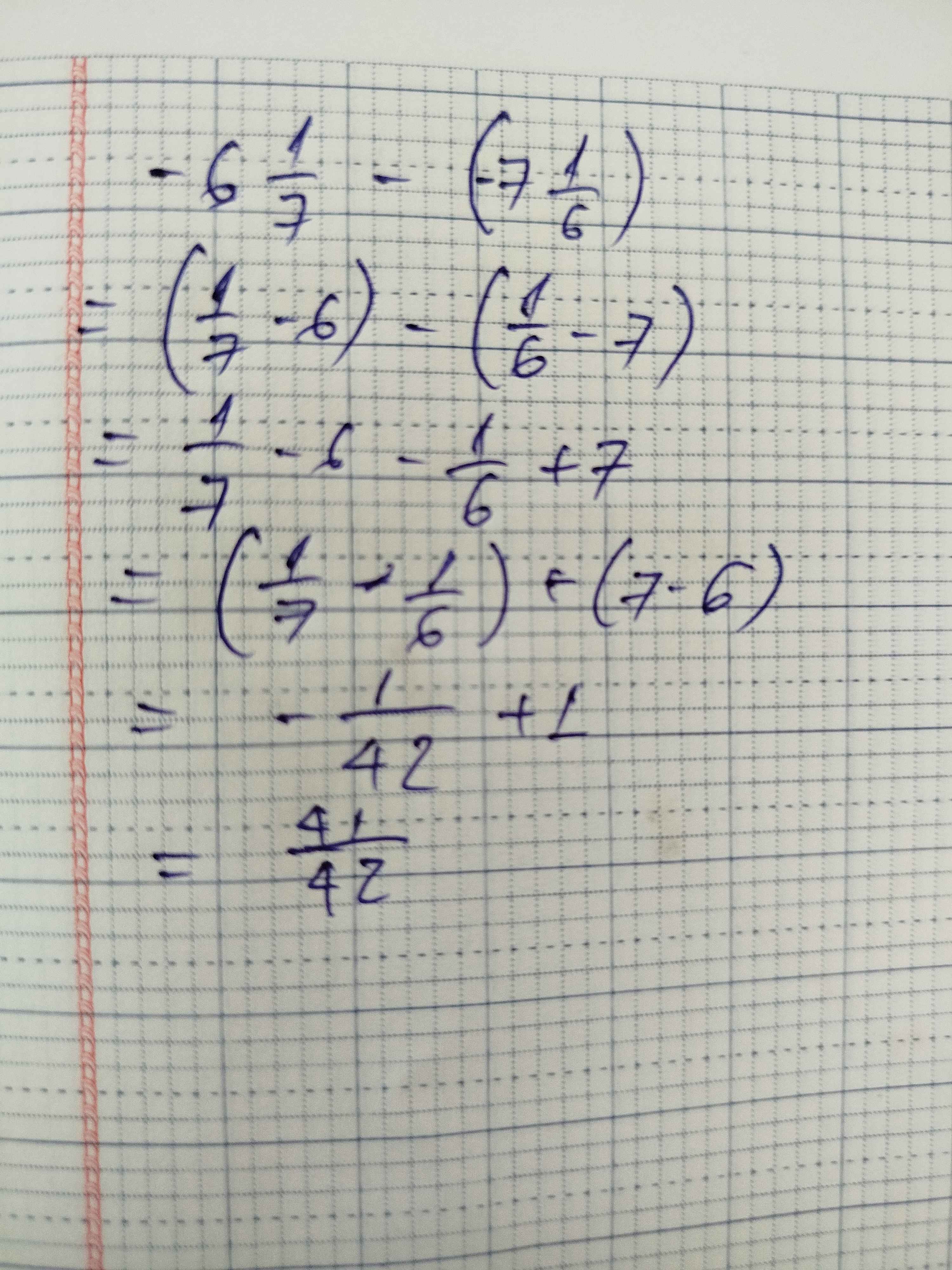
c: \(A=\left|-x+\dfrac{1}{7}\right|+\left|-x-\dfrac{3}{5}\right|-\dfrac{2}{6}\)

\(=\left|x-\dfrac{1}{7}\right|+\left|x+\dfrac{3}{5}\right|-\dfrac{1}{3}\)

\(-\dfrac{3}{5}< x< \dfrac{1}{7}\)

=>\(x+\dfrac{3}{5}>0;x-\dfrac{1}{7}< 0\)

=>\(A=\dfrac{1}{7}-x+x+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{1}{7}+\dfrac{3}{5}-\dfrac{1}{3}=\dfrac{43}{105}\)

d: \(A=\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|+8\dfrac{1}{5}\)

\(=\left|x-2\dfrac{1}{5}\right|+\left|x-\dfrac{1}{5}\right|+\dfrac{41}{5}\)

\(\dfrac{1}{5}< =x< =2\dfrac{1}{5}\)

=>\(x-\dfrac{1}{5}>=0;x-2\dfrac{1}{5}< =0\)

=>\(D=2\dfrac{1}{5}-x+x-\dfrac{1}{5}+\dfrac{41}{5}=2+\dfrac{41}{5}=\dfrac{51}{5}\)

Vì AB//CD

nên ΔMAB~ΔMCD

=>\(\dfrac{S_{MAB}}{S_{MCD}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)

=>\(\dfrac{S_{MAB}}{S_{ABCD}}=\dfrac{1}{8}\)

=>\(S_{MAB}=\dfrac{S_{ABCD}}{8}=3\left(cm^2\right)\)

\(B=\left(-\dfrac{1}{2}\right)+\left(-\dfrac{1}{6}\right)+\left(-\dfrac{1}{12}\right)+\left(-\dfrac{1}{20}\right)+\left(-\dfrac{1}{30}\right)+\left(-\dfrac{1}{42}\right)+\left(-\dfrac{1}{56}\right)+\left(-\dfrac{1}{72}\right)+\left(-\dfrac{1}{90}\right)\)

\(=-\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{90}\right)\)

\(=-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{9\cdot10}\right)\)

\(=-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)

\(=-\left(1-\dfrac{1}{10}\right)=-\dfrac{9}{10}\)

ĐKXĐ: x<>2

\(\dfrac{x-2}{8}=\dfrac{-2}{2-x}\cdot\dfrac{1}{3}\)

=>\(\dfrac{x-2}{8}=\dfrac{2}{x-2}\cdot\dfrac{1}{3}=\dfrac{2}{3\left(x-2\right)}\)

=>\(3\cdot\left(x-2\right)^2=16\)

=>\(\left(x-2\right)^2=\dfrac{16}{3}\)

=>\(\left[{}\begin{matrix}x-2=\dfrac{4}{\sqrt{3}}\\x-2=-\dfrac{4}{\sqrt{3}}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2+\dfrac{4}{\sqrt{3}}=2+\dfrac{4\sqrt{3}}{3}=\dfrac{6+4\sqrt{3}}{3}\\x=2-\dfrac{4}{\sqrt{3}}=\dfrac{6-4\sqrt{3}}{3}\end{matrix}\right.\)

1: \(\left|x-3,5\right|>=0\forall x\)

\(\left|4,5-y\right|>=0\forall y\)

Do đó: \(\left|x-3,5\right|+\left|4.5-y\right|>=0\forall x,y\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-3,5=0\\4,5-y=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=3,5\\y=4,5\end{matrix}\right.\)

2: \(\left\{{}\begin{matrix}\left|x+\dfrac{2}{3}\right|>=0\forall x\\\left|y-\dfrac{3}{4}\right|>=0\forall y\\\left|z-5\right|>=0\forall z\end{matrix}\right.\)

Do đó: \(\left|x+\dfrac{2}{3}\right|+\left|y-\dfrac{3}{4}\right|+\left|z-5\right|>=0\forall x,y,z\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+\dfrac{2}{3}=0\\y-\dfrac{3}{4}=0\\z-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{3}{4}\\z=5\end{matrix}\right.\)

3: \(\left|x-2\right|+\left|3-x\right|=0\)

=>|x-2|+|x-3|=0(1)

TH1: x<2

Phương trình (1) sẽ trở thành 2-x+3-x=0

=>5-2x=0

=>2x=5

=>x=2,5(loại)

TH2: 2<=x<3

Phương trình (1) sẽ trở thành x-2+3-x=0

=>1=0(loại)

TH3: x>=3

Phương trình (1) sẽ trở thành x-2+x-3=0

=>2x=5

=>x=2,5(loại)

Vậy: Phương trình vô nghiệm

4: \(\left\{{}\begin{matrix}\left|x-\dfrac{2}{3}\right|>=0\forall x\\\left|x+y+\dfrac{3}{4}\right|>=0\forall x,y\\\left|y-z-\dfrac{5}{6}\right|>=0\forall y,z\end{matrix}\right.\)

Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|x+y+\dfrac{3}{4}\right|+\left|y-z-\dfrac{5}{6}\right|>=0\forall x,y,z\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\x+y+\dfrac{3}{4}=0\\y-z-\dfrac{5}{6}=0\end{matrix}\right.\)

=>\(\begin{matrix}x=\dfrac{2}{3}\\y=-x-\dfrac{3}{4}=-\dfrac{2}{3}-\dfrac{3}{4}=\dfrac{-17}{12}\\z=y-\dfrac{5}{6}=-\dfrac{17}{12}-\dfrac{5}{6}=-\dfrac{27}{12}=-\dfrac{9}{4}\end{matrix}\)

5: \(\left\{{}\begin{matrix}\left|x-\dfrac{2}{3}\right|>=0\forall x\\\left|xy-\dfrac{5}{8}\right|>=0\forall x,y\\\left|yz+\dfrac{3}{4}\right|>=0\forall y,z\end{matrix}\right.\)

Do đó: \(\left|x-\dfrac{2}{3}\right|+\left|xy-\dfrac{5}{8}\right|+\left|yz+\dfrac{3}{4}\right|>=0\forall x,y,z\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{3}=0\\xy-\dfrac{5}{8}=0\\yz+\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\xy=\dfrac{5}{8}\\yz=-\dfrac{3}{4}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{5}{8}:x=\dfrac{5}{8}:\dfrac{2}{3}=\dfrac{5}{8}\cdot\dfrac{3}{2}=\dfrac{15}{16}\\z=-\dfrac{3}{4}:\dfrac{15}{16}=-\dfrac{3}{4}\cdot\dfrac{16}{15}=\dfrac{-48}{60}=-\dfrac{4}{5}\end{matrix}\right.\)

6: \(\left\{{}\begin{matrix}\left|xy+\dfrac{2}{3}\right|>=0\forall x,y\\\left|yz-\dfrac{8}{9}\right|>=0\forall y,z\\\left|xz+\dfrac{3}{4}\right|>=0\forall x,z\end{matrix}\right.\)

Do đó: \(\left|xy+\dfrac{2}{3}\right|+\left|yz-\dfrac{8}{9}\right|+\left|xz+\dfrac{3}{4}\right|>=0\forall x,y,z\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}xy+\dfrac{2}{3}=0\\yz-\dfrac{8}{9}=0\\xz+\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}xy=-\dfrac{2}{3}\\yz=\dfrac{8}{9}\\xz=-\dfrac{3}{4}\end{matrix}\right.\)

=>\(\left(xyz\right)^2=-\dfrac{2}{3}\cdot\dfrac{8}{9}\cdot\dfrac{-3}{4}=\dfrac{1}{2}\cdot\dfrac{8}{9}=\dfrac{4}{9}\)

=>\(\left[{}\begin{matrix}xyz=\dfrac{2}{3}\\xyz=-\dfrac{2}{3}\end{matrix}\right.\)

TH1: xyz=2/3

=>\(\left\{{}\begin{matrix}z=\dfrac{xyz}{xy}=\dfrac{2}{3}:\dfrac{-2}{3}=-1\\x=\dfrac{xyz}{yz}=\dfrac{2}{3}:\dfrac{8}{9}=\dfrac{2}{3}\cdot\dfrac{9}{8}=\dfrac{18}{24}=\dfrac{3}{4}\\y=\dfrac{xyz}{xz}=\dfrac{2}{3}:\dfrac{-3}{4}=\dfrac{2}{3}\cdot\dfrac{4}{-3}=-\dfrac{8}{9}\end{matrix}\right.\)

TH2: xyz=-2/3

=>\(\left\{{}\begin{matrix}z=\dfrac{xyz}{xy}=-\dfrac{2}{3}:\dfrac{-2}{3}=1\\x=\dfrac{xyz}{yz}=-\dfrac{2}{3}:\dfrac{8}{9}=\dfrac{-2}{3}\cdot\dfrac{9}{8}=\dfrac{-18}{24}=\dfrac{-3}{4}\\y=\dfrac{xyz}{xz}=\dfrac{-2}{3}:\dfrac{-3}{4}=\dfrac{-2}{3}\cdot\dfrac{4}{-3}=\dfrac{8}{9}\end{matrix}\right.\)

\(\dfrac{9}{5}< 2;\dfrac{7}{6}< \dfrac{29}{24};3>\dfrac{17}{18}\)

9/5< 2

Vì 10/5=2 mà 9/5<10/5

7/6<29/24

Quy đồng 7/6 và 29/24 ta được 28/24 và 29/24 mà 28/24<29/24

3>17/18

17/18<1 mà 3 > 1

Chúc cậu học tốt, thấy ok thì cho tớ xin một tim nhé!

Lời giải:

Chiều rộng khu đất: $2016:12=168$ (m) 

Tổng chiều dài và chiều rộng khu đất: $102:2=51$ (m) 

Bản thân chiều rộng khu đất còn lớn hơn cả tổng hai chiều, đề có vấn đề bạn xem lại nhé.

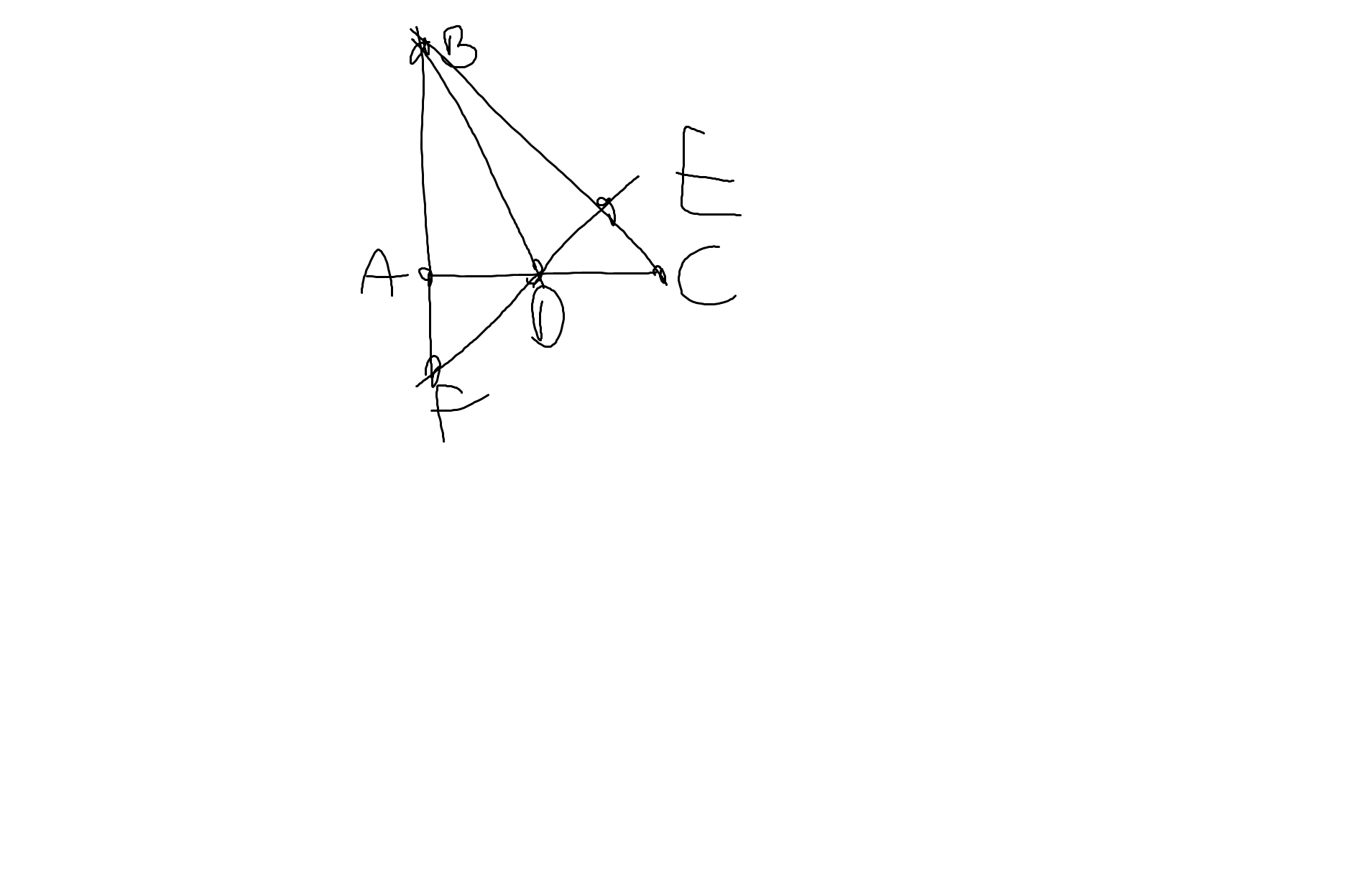
a: Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED
=>DA=DE

b: Ta có: BA=BE

=>B nằm trên đường trung trực của AE(1)

Ta có: DA=DE

=>D nằm trên đường trung trực của AE(2)

Từ (1),(2) suy ra BD là đường trung trực của AE

ΔBAD=ΔBED

=>\(\widehat{BAD}=\widehat{BED}\)

=>\(\widehat{BED}=90^0\)

=>DE\(\perp\)BC tại E

Ta có: ΔDEC vuông tại E

=>DC>DE

mà DE=DA

nên DC>DA

=>AD<DC

c: Ta có: BA+AF=BF

BE+EC=BC

mà BA=BE và BF=BC

nên AF=EC

Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

AF=EC

Do đó: ΔDAF=ΔDEC

=>\(\widehat{ADF}=\widehat{EDC}\)

=>\(\widehat{ADF}+\widehat{ADE}=180^0\)

=>F,D,E thẳng hàng

\(555+123=678\)

555+123=678