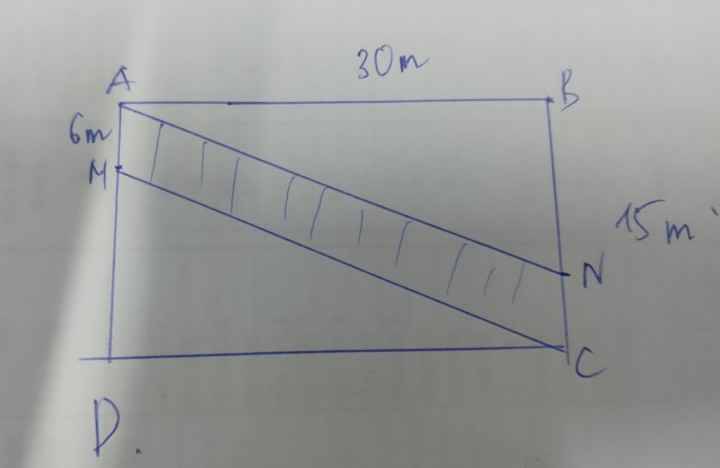
Cho tam giác ABC nhọn biết AB<AC . Các đường cao BE , CF cắt nhau tại H . Gọi M là trung điểm của BC . Trên tia đối của tia MH lấy K sao cho MH=MK .
a) cm tứ giác BHCK là hbh
b) cm BK vuông góc với AB , CK vuông góc với AC
c) cm tam giác MEF là tam giác cân
d) vẽ CQ vuông góc với BK tại Q . Chứng minh EF vuông góc với EQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ sơ đồ nha .
Tuổi của anh là :
\(\left(25+5\right):2=15\left(tuổi\right)\)
Tuổi của em là :
\(25-15\text{=}10\left(tuổi\right)\)
đs...........

Bạn có thể viết rõ hơn ra được không ạ . Chứ mình nhìn nó ra nhiều trường hợp lắm .

Bài 1 :
a) \(Cos30^o=Cos\left(2.15^o\right)=2cos^215^o-1\)
\(\Rightarrow cos^215^o=\dfrac{cos30^o+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\dfrac{\sqrt[]{3}}{2}+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\sqrt[]{3}+2}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\sqrt[]{3}+2}}{2}\)
\(\Rightarrow cos15^o=\dfrac{2\sqrt[]{\sqrt[]{3}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{4\sqrt[]{3}+8}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6+2.2\sqrt[]{2}\sqrt[]{6}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\left(\sqrt[]{6}+\sqrt[]{2}\right)^2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6}+\sqrt[]{2}^{ }}{4}\left(dpcm\right)\)
a)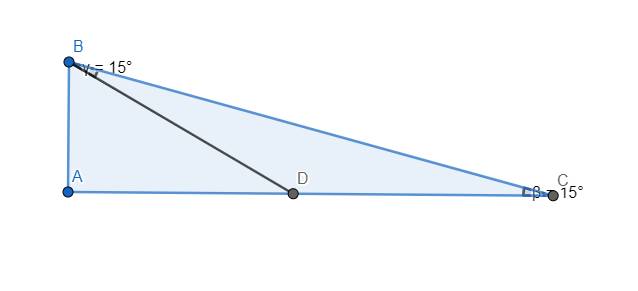
Dựng tam giác ABC vuông tại A với \(\widehat{C}=15^o\). Trên đoạn thẳng AC lấy điểm D sao cho \(\widehat{CBD}=15^o\). Không mất tính tổng quát, ta chuẩn hóa \(AB=1\). \(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{AB}{cos60^o}=2\\AD=AB.tan60^o=\sqrt{3}\end{matrix}\right.\)
Dễ thấy tam giác DBC cân tại D \(\Rightarrow BD=CD=2\) \(\Rightarrow AC=AD+DC=2+\sqrt{3}\)
\(\Rightarrow tanC=\dfrac{AB}{AC}=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
\(\Rightarrow\dfrac{sinC}{cosC}=2-\sqrt{3}\)
\(\Rightarrow sinC=\left(2-\sqrt{3}\right)cosC\)
Mà \(sin^2C+cos^2C=1\)
\(\Rightarrow\left(7-4\sqrt{3}\right)cos^2C+cos^2C=1\)
\(\Leftrightarrow\left(8-4\sqrt{3}\right)cos^2C=1\)
\(\Leftrightarrow cos^2C=\dfrac{1}{8-4\sqrt{3}}=\dfrac{2+\sqrt{3}}{4}\)
\(\Leftrightarrow cosC=\sqrt{\dfrac{2+\sqrt{3}}{4}}\) \(=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{8+4\sqrt{3}}}{4}\) \(=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)

Công thức tính số hạng là : Số đầu trừ số cuối chia khoảng cách cộng 1 .
Ta thấy dãy số : 1;2;3;...... là các số tự nhiên liên tiếp có khoảng cách là 1 đơn vị .
Do đó : Gọi số thứ 659 là : x
\(\Rightarrow x-1+1=659\)
\(\Rightarrow x=659\)
Vậy..........

Tổng số phần bằng nhau là:
4+3=7(phần)
Số học sinh nam là:
1470:7x4=840(học sinh)
Số học sinh nữ là:
1470-840=630(học sinh)
Đáp số: nam 840 học sinh
nữ 630 học sinh

=>\(x^2\)+ \(7x\)=3\(x^2\)+\(7x\)-5
=>\(-2x^2\)+5=0
=>2\(x^2\)-5=0
=>2\(x^2\)=5
=>\(x^2\)=\(\dfrac{5}{2}\)
=>\(x\)=-\(\sqrt{\dfrac{5}{2}}\)
=>\(x\)=+\(\sqrt{\dfrac{5}{2}}\)

\(\dfrac{20}{32}\)=x+\(\dfrac{9}{24}\)
=>x=\(\dfrac{20}{32}\)-\(\dfrac{9}{24}\)
=>x=\(\dfrac{20.3-9.4}{96}\)
=>x=\(\dfrac{60-36}{96}\)
==>x=\(\dfrac{24}{96}\)
=>x=\(\dfrac{1}{4}\)

`@` `\text {Ans}`
`\downarrow`
\(5^{x-2}-3^2=2^4-\left(6^8\div6^6-6^2\right)\)
`\Rightarrow`\(5^x\div5^2-9=16-\left(6^2-6^2\right)\)
`\Rightarrow`\(5^x\div5^2-9=16\)
`\Rightarrow`\(5^x\div5^2=25\)
`\Rightarrow`\(5^x=5^2\cdot5^2\)
`\Rightarrow`\(5^x=5^4\Rightarrow x=4\)
Vậy, `x = 4.`
5ˣ⁻² - 3² = 2⁴ - (6⁸ : 6⁶ - 6²)
5ˣ⁻² - 9 = 16 - (36 - 36)
5ˣ⁻² - 9 = 16
5ˣ⁻² = 16 + 9
5ˣ⁻² = 25
5ˣ⁻² = 5²
x - 2 = 2
x = 2 + 2
x = 4