-11/15 = -6/15 + (-5/15) = -2/5 + (-1/3)

-11/15 = -1/15 + (-10/15) = -1/15 + (-2/3)

-11/15 = -4/15 + (-7/15)

\(x^2-25=y\left(y+6\right)\)

\(\Leftrightarrow x^2-25=y^2+6y\)

\(\Leftrightarrow x^2-25-y^2-6y=0\)

\(\Leftrightarrow x^2-\left(y^2+6y+9\right)-16=0\)

\(\Leftrightarrow x^2-\left(y+3\right)^2=16\)

\(\Leftrightarrow\left(x+y+3\right)\left(x-y-3\right)=16\)

\(\Leftrightarrow\left(x+y+3\right);\left(x-y-3\right)\in\left\{-1;1;-2;2;-4;4;-8;8;-16;16\right\}\)

Ta giải các hệ phương trình sau :

1) \(\left\{{}\begin{matrix}x+y+3=-1\\x-y-3=-16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-4\\x-y=-15\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x=-11\left(loại\right)\\x-y=-15\end{matrix}\right.\)

2) \(\left\{{}\begin{matrix}x+y+3=1\\x-y-3=16\end{matrix}\right.\)  \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-2\\x-y=19\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=17\left(loại\right)\\x-y=19\end{matrix}\right.\)

3) \(\left\{{}\begin{matrix}x+y+3=2\\x-y-3=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\x-y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=10\\x-y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-6\end{matrix}\right.\)

4) \(\left\{{}\begin{matrix}x+y+3=-2\\x-y-3=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-5\\x-y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-10\\x-y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=0\end{matrix}\right.\)

5) \(\left\{{}\begin{matrix}x+y+3=-4\\x-y-3=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-7\\x-y=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-6\\x-y=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)

6) \(\left\{{}\begin{matrix}x+y+3=4\\x-y-3=4\end{matrix}\right.\)  \(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x-y=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=8\\x-y=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-3\end{matrix}\right.\)

7) \(\left\{{}\begin{matrix}x+y+3=-8\\x-y-3=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-11\\x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-10\\x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=-6\end{matrix}\right.\)

8) \(\left\{{}\begin{matrix}x+y+3=8\\x-y-3=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\x-y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=10\\x-y=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=0\end{matrix}\right.\)

9) \(\left\{{}\begin{matrix}x+y+3=-16\\x-y-3=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-19\\x-y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-17\left(loại\right)\\x-y=2\end{matrix}\right.\)

10) \(\left\{{}\begin{matrix}x+y+3=16\\x-y-3=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=15\\x-y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=19\left(loại\right)\\x-y=4\end{matrix}\right.\)

Vậy \(\left(x;y\right)\in\left\{\left(5;-6\right);\left(-5;0\right);\left(-3;-2\right);\left(4;-3\right);\left(-5;-6\right);\left(5;0\right)\right\}\)

a) 3/8 = 1/8 + 2/8 = 1/8 + 1/4

3/8 = 5/8 - 2/8 = 5/8 - 1/4

b) 5/12 = 1/12 + 4/12 = 1/12 + 1/3

5/12 = 7/12 - 2/12 = 7/12 - 1/6

c) 1/11 = -2/11 + 3/11

1/11 = 2/11 - 1/11

d) 1/4 = -2/4 + 3/4 = -1/2 + 3/4

1/4 = 5/4 - 4/4 = 5/4 -1

a, \(\dfrac{1}{2}\) - ( - \(\dfrac{1}{3}\) ) + \(\dfrac{1}{23}\) + \(\dfrac{1}{6}\)

 =  \(\dfrac{5}{6}\)  + \(\dfrac{1}{23}\) + \(\dfrac{1}{6}\)

= 1 + \(\dfrac{1}{23}\)

 = \(\dfrac{24}{23}\) 

b, \(\dfrac{11}{24}\) - \(\dfrac{5}{41}\) + \(\dfrac{13}{24}\) + 0,5 - \(\dfrac{36}{41}\)

= (\(\dfrac{11}{24}\) + \(\dfrac{13}{24}\)) - ( \(\dfrac{5}{41}\) + \(\dfrac{36}{41}\)) + 0,5

= 1 - 1 + 0,5

= 0,5 

c,\(-\dfrac{1}{12}-\left(\dfrac{1}{6}-\dfrac{1}{4}\right)\)

=\(-\dfrac{1}{12}-\left(-\dfrac{1}{12}\right)\)

=0

d, \(\dfrac{1}{6}-\left[\dfrac{1}{6}-\left(\dfrac{1}{4}+\dfrac{9}{12}\right)\right]\)

= \(\dfrac{1}{6}-\left[\dfrac{1}{6}-1\right]\)

= \(\dfrac{1}{6}-\left(-\dfrac{5}{6}\right)\)

= 1

Rút gọn: \(\dfrac{28}{-6}=\dfrac{14}{3}\)

Quy đồng: \(-5=-\dfrac{15}{3}\)

Vì \(14>-15\) nên \(\dfrac{28}{-6}>-5\)

\(\dfrac{28}{6}=\dfrac{30-2}{6}=5-\dfrac{2}{6}=5-\dfrac{1}{3}< 5\)

\(\Rightarrow\dfrac{28}{6}< 5\Rightarrow-\dfrac{28}{6}>-5\Rightarrow\dfrac{28}{-6}>-5\)

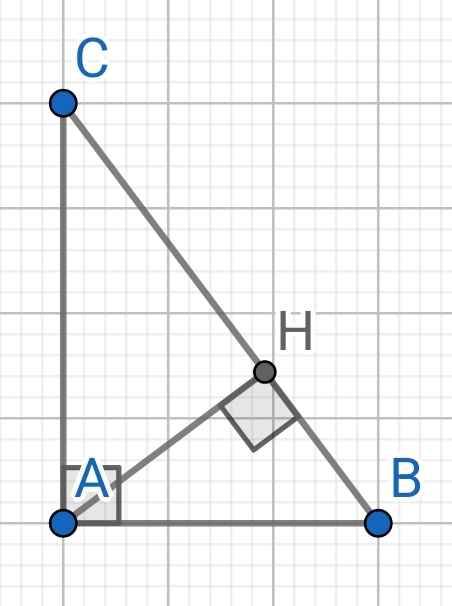 a) ∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AB² = BC.BH

⇒ BH = AB²/BC

= 6²/10

= 3,6 (cm)

⇒ HC = BC - BH

= 10 - 3,6

= 6,4 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AH.BC = AB.AC

⇒ AH = AB.AC/BC

= 6.8/10

= 4,8 (cm)

b) Ta có:

BC = BH + CH

= 12 + 27

= 29 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AB² = BC.BH

= 29.12

= 348

⇒ AB = 2√87

∆ABC vuông tại A, AH là đường cao

⇒ AC² = BC.CH

= 29.17

= 493

⇒ AC = √493 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AH² = BH.HC

= 12.17

= 204

⇒ AH = 2√51 (cm)

a) \(BC^2=AB^2+AC^2=64+36=100\left(Pitago\right)\)

\(\Rightarrow BC=10\left(cm\right)\)

\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{64}{10}=\dfrac{32}{5}\left(cm\right)\)

\(AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}\left(cm\right)\)

\(AH^2=BH.CH=\dfrac{32}{5}.\dfrac{18}{5}=\dfrac{576}{25}\Rightarrow AH=\dfrac{24}{5}\left(cm\right)\)

b) \(AH^2=BH.CH=12.27=324\Rightarrow AH=18\left(cm\right)\)

\(BC=BH+HC=12+27=39\left(cm\right)\)

\(AB^2=BH.BC=12.39=468\Rightarrow AB=\sqrt[]{468}=6\sqrt[]{13}\left(cm\right)\)

\(AC^2=CH.BC=27.39=1053\Rightarrow AC=\sqrt[]{1053}=9\sqrt[]{13}\left(cm\right)\)

4dm³ 25 cm³ = 4025 cm³

Thể tích hình thứ hai là 

4025 x \(\dfrac{3}{5}\) =  2415 (cm³)

Đáp số 2415 cm³

4 dm³ 25 cm³ = 4025 cm³

Thể tích hình thứ hai:

4025 × 3/5 = 2415 (cm³)