 GIÚP MIK VỚI ! NHANH NHA
GIÚP MIK VỚI ! NHANH NHA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(\dfrac{-2}{3}+\dfrac{3}{4}-\dfrac{-1}{6}+\dfrac{-2}{5}\)
\(=-\dfrac{40}{60}+\dfrac{45}{60}+\dfrac{10}{60}-\dfrac{24}{60}\)
\(=\dfrac{5-14}{60}=-\dfrac{9}{60}=-\dfrac{3}{20}\)
2: \(\dfrac{-2}{3}+\dfrac{-1}{5}+\dfrac{3}{4}-\dfrac{5}{6}-\dfrac{-7}{10}\)
\(=\left(-\dfrac{2}{3}+\dfrac{3}{4}-\dfrac{5}{6}\right)+\left(-\dfrac{1}{5}+\dfrac{7}{10}\right)\)
\(=\left(-\dfrac{8}{12}+\dfrac{9}{12}-\dfrac{10}{12}\right)+\left(-\dfrac{2}{10}+\dfrac{7}{10}\right)\)
\(=\dfrac{-9}{12}+\dfrac{5}{10}=-\dfrac{3}{4}+\dfrac{1}{2}=-\dfrac{3}{4}+\dfrac{2}{4}=-\dfrac{1}{4}\)
3: \(\dfrac{1}{2}-\dfrac{-2}{5}+\dfrac{1}{3}+\dfrac{5}{7}-\dfrac{-1}{6}+\dfrac{-4}{35}+\dfrac{1}{41}\)
\(=\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}\right)+\left(\dfrac{2}{5}+\dfrac{5}{7}-\dfrac{4}{35}\right)+\dfrac{1}{41}\)
\(=\dfrac{3+2+1}{6}+\dfrac{14+25-4}{35}+\dfrac{1}{41}\)
\(=\dfrac{6}{6}+\dfrac{35}{35}+\dfrac{1}{41}=2+\dfrac{1}{41}=\dfrac{83}{41}\)
4: \(\dfrac{1}{100\cdot99}-\dfrac{1}{99\cdot98}-\dfrac{1}{98\cdot97}-...-\dfrac{1}{3\cdot2}-\dfrac{1}{2\cdot1}\)
\(=\dfrac{1}{100\cdot99}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{97\cdot98}+\dfrac{1}{98\cdot99}\right)\)
\(=\dfrac{1}{100\cdot99}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{98}-\dfrac{1}{99}\right)\)
\(=\dfrac{1}{99}-\dfrac{1}{100}-\dfrac{98}{99}=\dfrac{-97}{99}-\dfrac{1}{100}=\dfrac{-9799}{9900}\)
5: \(\dfrac{\left(\dfrac{3}{10}-\dfrac{4}{15}-\dfrac{7}{20}\right)\cdot\dfrac{5}{19}}{\left(\dfrac{1}{14}+\dfrac{1}{7}-\dfrac{-3}{35}\right)\cdot\dfrac{-4}{3}}=\dfrac{\dfrac{18-16-21}{60}\cdot\dfrac{5}{19}}{\dfrac{5+10+6}{70}\cdot\dfrac{-4}{3}}\)
\(=\dfrac{\dfrac{-19}{60}\cdot\dfrac{5}{19}}{\dfrac{21}{70}\cdot\dfrac{-4}{3}}=\dfrac{-5}{60}:\dfrac{-84}{210}=\dfrac{-1}{12}\cdot\dfrac{-5}{2}=\dfrac{5}{24}\)
6: \(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{4}{4}=1\)

Gọi số cần tìm có dạng là \(\overline{ab}\)
Nếu viết thêm chữ số 0 vào giữa hai chữ số thì ta được số mới gấp 6 lần số cũ nên \(\overline{a0b}=6\cdot\overline{ab}\)
=>\(100a+b=6\cdot\left(10a+b\right)\)
=>100a+b=60a+6b
=>40a=5b
=>8a=b
=>b=8; a=1
Vậy: Số cần tìm là 18

a: Để hệ có nghiệm duy nhất thì \(\dfrac{3}{2}\ne\dfrac{a}{1}\)
=>\(a\ne1,5\)
b: Để hệ vô nghiệm thì \(\dfrac{3}{2}=\dfrac{a}{1}\ne\dfrac{5}{b}\)
=>\(\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b\ne\dfrac{10}{3}\end{matrix}\right.\)
c: Để hệ có vô số nghiệm thì \(\dfrac{3}{2}=\dfrac{a}{1}=\dfrac{5}{b}\)
=>\(\left\{{}\begin{matrix}a=1\cdot\dfrac{3}{2}=\dfrac{3}{2}\\b=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\end{matrix}\right.\)

Bài 7:
a: \(\dfrac{11}{13}=\dfrac{110}{130};\dfrac{12}{13}=\dfrac{120}{130}\)
=>4 phân số nằm giữa 11/13 và 12/13 là \(\dfrac{111}{130};\dfrac{112}{130};\dfrac{113}{130};\dfrac{116}{130}\)
b: \(\dfrac{15}{17}=\dfrac{150}{170};\dfrac{15}{16}=\dfrac{150}{160}\)
=>5 phân số nằm giữa 15/17 và 15/16 là \(\dfrac{150}{169};\dfrac{150}{168};\dfrac{150}{167};\dfrac{150}{165};\dfrac{150}{153}\)

Bài 11:
\(a)x\times12,8=6,4\\ x=6,4:12,8\\ x=\dfrac{1}{2}\\ b)17,3:x=69,2\\ x=17,3:69,2\\ x=\dfrac{1}{4}\\ c)16,48\times x=4,12\\ x=4,12:16,48\\ x=\dfrac{1}{4}\\ d)x:12,8=1,6\\ x=12,8\times1,6\\ x=\dfrac{512}{25}\)
Bài 11:
a: \(x\times12,8=6,4\)
=>\(x=\dfrac{6.4}{12.8}=\dfrac{1}{2}=0,5\)
b: \(17,3:x=69,2\)
=>\(x=\dfrac{17.3}{69.2}=0,25\)
c: \(16,48\times x=4,12\)
=>\(x=\dfrac{4.12}{16.48}=\dfrac{1}{4}=0,25\)
d: \(x:12,8=1,6\)
=>\(x=12,8\times1,6=20,48\)
Bài 9:
a: \(4,86\times0,25\times40=4,86\times10=48,6\)
b: \(0,125\times6,94\times80=6,94\times\left(80\times0,125\right)\)
=6,94x10
=69,4
c: \(96,28\times3,527+3,527\times3,72\)
=3,527x(96,28+3,72)
=3,527x100=352,7
d: \(72,9\times99+72+0,9\)
=72,9x99+72,9
=72,9x(99+1)
=72,9x100=7290
e: \(0,8\times96+1,6\times2\)
\(=0,8\times96+0,8\times4=0,8\times\left(96+4\right)\)
=0,8x100=80

\(D=x^2+y^2-x+6y+10\\ =\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}\\ =\left(x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}\right)+\left(y^2+2\cdot y\cdot3+3^2\right)+\dfrac{3}{4}\\ =\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\)
Ta có: \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\\\left(y+3\right)^2\ge0\forall y\end{matrix}\right.=>D=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x,y\)
Dấu "=" xảy ra \(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
______________________________
\(F=2xy-2x^2-y^2+10x-27\\ =-\left(x^2-2xy+y^2\right)-\left(x^2-10x+25\right)-2\\ =-\left(x-y\right)^2-\left(x-5\right)^2-2\)
Ta có: \(\left\{{}\begin{matrix}\left(x-y\right)^2\le0\forall x,y\\-\left(x-5\right)^2\le0\forall x\end{matrix}\right.=>F=-\left(x-y\right)^2-\left(x-5\right)^2-2\le-2\forall x,y\)
Dấu "=" xảy ra: \(\left\{{}\begin{matrix}x-y=0\\x-5=0\end{matrix}\right.\Leftrightarrow x=y=5\)
\(A=-x^2+x-1\)
\(=-\left(x^2-x+1\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}< =-\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
\(B=6x-x^2-10\)
\(=-\left(x^2-6x+10\right)\)
\(=-\left(x^2-6x+9+1\right)\)
\(=-\left(x-3\right)^2-1< =-1\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
\(C=-x^2+5x+3\)
\(=-\left(x^2-5x-3\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{37}{4}\right)\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{37}{4}< =\dfrac{37}{4}\forall x\)
Dấu '=' xảy ra khi x-5/2=0
=>x=5/2
\(D=x^2-x+y^2+6y+10\)
\(=x^2-x+\dfrac{1}{4}+y^2+6y+9+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
\(F=2xy-2x^2-y^2+10x-27\)
\(=-\left(2x^2+y^2-2xy-10x+27\right)\)
\(=-\left(x^2-2xy+y^2+x^2-10x+25+2\right)\)
\(=-\left(x-y\right)^2-\left(x-5\right)^2-2< =-2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=x=5\end{matrix}\right.\)

Bài 1:
\(a)\left(\dfrac{1}{3}:x-1\right)=\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{21}\\ \dfrac{1}{3}:x-1=\dfrac{7}{21}+\dfrac{3}{21}-\dfrac{1}{21}=\dfrac{9}{21}\\ \dfrac{1}{3}:x-1=\dfrac{3}{7}\\ \dfrac{1}{3}:x=\dfrac{3}{7}+1=\dfrac{10}{7}\\ x=\dfrac{1}{3}:\dfrac{10}{7}\\ x=\dfrac{7}{30}\\ b)\dfrac{1}{5}\cdot x-\dfrac{2}{13}=\dfrac{1}{2\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{3}{5\cdot8}+\dfrac{5}{8\cdot13}\\ \dfrac{1}{5}\cdot x-\dfrac{2}{13}=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{13}\\ \dfrac{1}{5}\cdot x-\dfrac{2}{13}=\dfrac{1}{2}-\dfrac{1}{13}=\dfrac{11}{26}\\\dfrac{1}{5}\cdot x=\dfrac{11}{26}+\dfrac{2}{13}=\dfrac{15}{26}\\ x=\dfrac{15}{26}:\dfrac{1}{5}=\dfrac{75}{26}\\c)\dfrac{13}{6} :\left(\dfrac{1}{2}+x\right)=\dfrac{1}{3}+\dfrac{3}{7}+\dfrac{1}{7\cdot2}+\dfrac{5}{2\cdot13}+\dfrac{3}{13\cdot4}\\ \dfrac{13}{6}:\left(\dfrac{1}{2}+x\right)=\dfrac{1}{3}+\left(\dfrac{3}{7}+\dfrac{1}{7\cdot2}\right)+\left(\dfrac{5}{2\cdot13}+\dfrac{3}{13\cdot4}\right)\\ \dfrac{13}{6}:\left(\dfrac{1}{2}+x\right)=\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{1}{4}\\ \dfrac{13}{6}:\left(\dfrac{1}{2}+x\right)=\dfrac{13}{12}\\ \dfrac{1}{2}+x=\dfrac{13}{6}:\dfrac{13}{12}=2\\ x=2-\dfrac{1}{2}\\ x=\dfrac{3}{2}\)

 câu 7 thui
câu 7 thui
 giúp mk làm bài 7 thôi còn bài 1 đến 6 ko cần đâu
giúp mk làm bài 7 thôi còn bài 1 đến 6 ko cần đâu
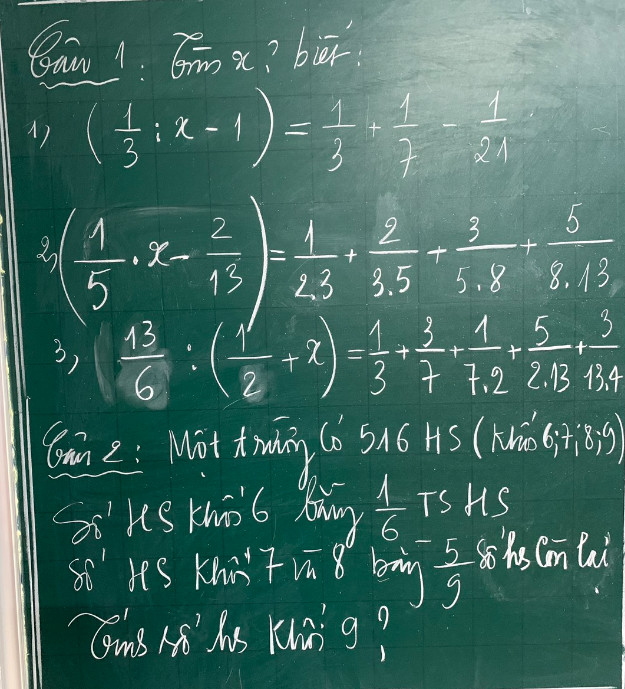
Bài 3:
a: ĐKXĐ: \(x\ne-1\)
Để A là số nguyên thì \(4⋮x+1\)
=>\(x+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{0;-2;1;-3;3;-5\right\}\)
b: DKXĐ: x<>-1
Để B là số nguyên thì \(x+3⋮x+1\)
=>\(x+1+2⋮x+1\)
=>\(2⋮x+1\)
=>\(x+1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{0;-2;1;-3\right\}\)
c: ĐKXĐ: x<>2
Để C là số nguyên thì \(x-5⋮x-2\)
=>\(x-2-3⋮x-2\)
=>\(-3⋮x-2\)
=>\(x-2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{3;1;5;-1\right\}\)
d: ĐKXĐ: x<>-1/2
Để D là số nguyên thì \(4x-3⋮2x+1\)
=>\(4x+2-5⋮2x+1\)
=>\(-5⋮2x+1\)
=>\(2x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-1;2;-3\right\}\)
Bài 4:
a: ĐKXĐ: \(x\ne0\)
Để \(\dfrac{3}{x}>0\) thì x>0
b: ĐKXĐ: \(x\ne0\)
Để \(\dfrac{4}{3x}>0\) thì 3x>0
=>x>0
c: ĐKXĐ: \(x\ne-1\)
Để \(\dfrac{2}{x+1}>0\) thì x+1>0
=>x>-1
d: ĐKXĐ: \(x\ne2\)
Để \(-\dfrac{1}{x-2}\)>0 thì x-2<0
=>x<2
e: ĐKXĐ: \(x\ne-4\)
Để \(\dfrac{x}{x+4}>0\) thì \(\left[{}\begin{matrix}\left\{{}\begin{matrix}x>0\\x+4>0\end{matrix}\right.\\\left\{{}\begin{matrix}x< 0\\x+4< 0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x>0\\x< -4\end{matrix}\right.\)