(1 điểm) Người ta dùng một mặt phẳng nghiêng có chiều dài 5 m để kéo một vật có khối lượng 300 kg với lực kéo 1200 N . Biết hiệu suất của mặt phẳng nghiêng là 80%. Tính chiều cao của mặt phẳng nghiêng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn mốc thế năng tại mặt đất.
Gọi A là vị trí ném, B là mặt đất, ta có:
a. Theo định luật bảo toàn cơ năng:
m/s
b. Gọi C là vị trí có
Theo định luật bảo toàn cơ năng:
m.
c. Gọi D là vị trí để vật có vận tốc 20 m/s.
Theo định luật bảo toàn cơ năng:
m
Vậy tại vị trí cách mặt đất 25 m thì vật có vận tốc 20 m/s.
Chọn mốc thế năng tại mặt đất.
Gọi A là vị trí ném, B là mặt đất, ta có:
a. Theo định luật bảo toàn cơ năng:
m/s
b. Gọi C là vị trí có
Theo định luật bảo toàn cơ năng:
m.
c. Gọi D là vị trí để vật có vận tốc 20 m/s.
Theo định luật bảo toàn cơ năng:
m
Vậy tại vị trí cách mặt đất 25 m thì vật có vận tốc 20 m/s.

Chọn mốc thế năng ở mặt đất
Ta có : \(\left\{{}\begin{matrix}W=W_đ+W_t\\W_đ=1,5.W_t\end{matrix}\right.\) \(\Leftrightarrow W=2,5W_t=2,5.m.g.z\)
\(\Leftrightarrow m=\dfrac{W}{2,5.g.z}=\dfrac{37,5}{2,5.10.3}=0,5\left(kg\right)\)
tương tự \(W=\dfrac{5}{3}W_đ=\dfrac{5}{3}.\dfrac{1}{2}.m.v_0^2\)
Vận tốc vật là : \(v_0=\pm\sqrt{\dfrac{W}{\dfrac{5}{6}m}}=\pm3\sqrt{10}\)(m/s)
Chọn mốc thế năng tại mặt đất
Theo định luật bảo toàn năng lượng
Ta có
⇒v=√3.gz≈9,49(m/s)
tự

Đổi: 21,6 km/h = 6 m/s
m = 2 tấn = 2000kg
Ta có Vt = Vo + at
=> a = (Vt - Vo) / t = (6-0) / 15 = 0,4 m/s^2
Quãng đường xe đi được là:
S = (Vt^2 - Vo^2) / 2a = (6^2-0^2) / 2.0,4 = 45m
a) Ta có: F = ma = 2000.0,4 = 800 N
A = F.S = 800.45 = 36000 J
P = A / t = 36000 / 15 = 240 W
b) Ta có Fms = 0,005.N = 0,005.2000.10 = 1000 N
ADĐL II Newton: F - Fms = ma
=> F = Fms + ma = 1000 + 2000.0,4 = 1800 N
A = F.S = 1800.45 = 81000 J
P = A / t = 81000 / 15 = 5400 W

f(0)=2014=a.0^2+b.0+c=c => c=2014
f(1)=2015= a.1^2+b.1+c = a+b+c=a+b+2014 => a+b=2015-2014=1 (*)
f(-1)=2017=a.(-1)^2+b.(-1)+c= a-b+c=a-b+2014 =>a-b=2017-2014=3(**)
từ (*) và (**) ta có hệ pt và tính được a=2 và b= -1
=> f(-2) = 2.(-2)^2 + (-1).(-2) +2014=2024
F(0) = a.02 + b. 0 + c = 2014 => c = 2014
F(1) = a.12 + b. 1+ 2014 = 2015 => a + b = 2015 - 2014 = 1
F(-1) = a.(-1)2 + b.(-1) + 2014 = 2017 = > a - b = 2017 - 2014 = 3
Cộng vế cho vế ta được : 2a = 1 + 3 = 4=> a = 4/2 =2
thay a = 2 vào a + b = 1 ta có
2 + b = 1 => b = -1
F(x) = 2x2 - x + 2014
Vậy F(-2) = 2. (-2)2 - (-2) + 2014 = 2024

Hàm là \(y=mx^2-\left(m^2+1\right)x+3\) đúng không nhỉ?
- Với \(m=0\) hàm nghịch biến trên R (không thỏa)
- Với \(m\ne0\) hàm số đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}m>0\\\dfrac{m^2+1}{2m}\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>0\\m^2+1\le2m\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m>0\\\left(m-1\right)^2\le0\end{matrix}\right.\)
\(\Rightarrow m=1\)

đt△ x + 4y - 2 = 0 => y = -\(\dfrac{1}{4}\)x + \(\dfrac{1}{2}\)
Đt d có dạng y = ax + b vì (d) //Δ nên a = -\(\dfrac{1}{4}\); b # \(\dfrac{1}{2}\)
đt (d) có dạng y = \(-\dfrac{1}{4}\) x + b ⇒x+ 4y - 4b = 0
Khoảng cách từ A(-2;3) đến đường thẳng (d) là :
d(A;d) = \(\dfrac{|-2+4.3-4b|}{\sqrt{1^2+4^2}}\) = 3
| 10 - 4b| = 3\(\sqrt{17}\)
10- 4b = 3\(\sqrt{17}\)
b = \(\dfrac{10-3\sqrt{17}}{4}\)
4b - 10 = 3\(\sqrt{17}\)
b = \(\dfrac{10+3\sqrt{17}}{4}\)
pt đt d thỏa mãn đề bài là:
y = - \(\dfrac{1}{4}\) x + \(\dfrac{10-3\sqrt{17}}{4}\) hoặc y = \(-\dfrac{1}{4}\) x + \(\dfrac{10+3\sqrt{17}}{4}\)

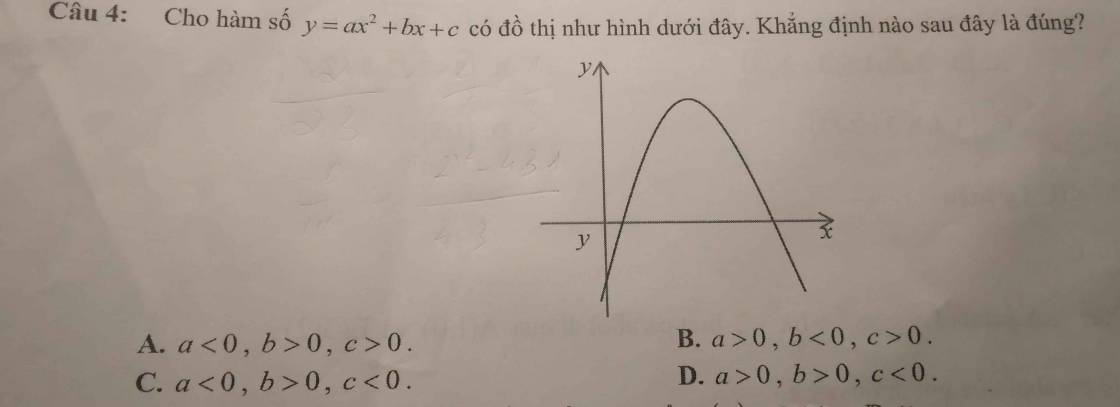
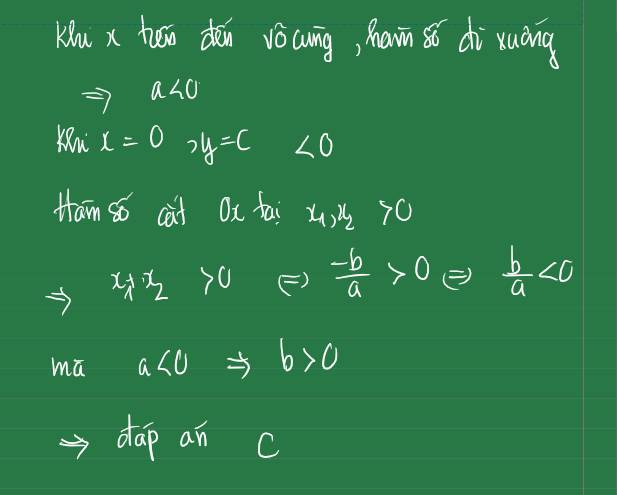

Ta có
`H = A_i/A_(tp)`
`<=> H = (10m*h)/(F*l)`
`<=> 80%=(10*300*h)/(1200*5)`
`=> h=1,6m`
Công toàn phần là:
Atp=Fl=1200.5=6000J
Công có ích là:
Ai=Atp.H=6000.80%=4800J
Chiều cao của mặt phẳng nghiêng là:
h=AiP=4800300.10=1,6(m)
Câu 6:
Quãng đường xe đi được là:
s=AF=360.103600=600(m)
Tốc độ của xe là:
v=st=6005.60=2(m/s)