Nếu tứ giác abcd một cặp cạnh đối song song thì tứ giác abcd là hình bình hành đúng hay sai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(sina=\dfrac{2}{3}\left(0< a< 90^o\right)\)
\(sin^2a+cos^2b=1\Rightarrow cos^2a=1-sin^2a=1-\dfrac{4}{9}=\dfrac{5}{9}\)
\(\Rightarrow cosa=\dfrac{\sqrt{5}}{3}\left(0< a< 90^o\Rightarrow cosa>0\right)\)
\(tana=\dfrac{sina}{cosa}=\dfrac{\dfrac{2}{3}}{\dfrac{\sqrt{5}}{3}}=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(P=tana-3cosa=\dfrac{2\sqrt{5}}{5}-3.\dfrac{\sqrt{5}}{3}=\dfrac{2\sqrt{5}}{5}-\sqrt{5}=\dfrac{-3\sqrt{5}}{5}\)

Bài 2:
a) Mệnh đề phủ định là: \("\exists x\in R;n⋮̸n"\)
Mà `n⋮n` với mọi n => Mệnh đề sai
b) Mệnh đề phủ định là: \("\forall x\in Q;x^2\ne2"\)
Ta có: \(x^2\ne2\Leftrightarrow x\ne\pm\sqrt{2}\)
Mà: \(\pm\sqrt{2}\notin Q\) => Mệnh đề đúng
c) Mệnh đề phủ định là: \("\exists x\in R;x\ge x+1"\)
Mà: `x<x+1` với mọi x
`=>` Mệnh đề sai
d) Mệnh đề phủ định là \("\forall x\in R;3x=x^2+1"\)
Ta có: `3x=x^2+1`
`<=>x^2-3x+1=0`
\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0=>\left[{}\begin{matrix}x=\dfrac{3-\sqrt{5}}{2}\\x=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
=> `3x=x^2+1` chỉ đúng với 2 giá trị
=> Mệnh đề sai
Bài 1: "\(\forall x\in R;\exists y\in R;y=x+3\)"
=>Mệnh đề này đúng vì với mọi giá trị của x luôn tồn tại một giá trị của y sao cho y=x+3
Mệnh đề phủ định là: "\(\exists x\in R;\forall y\in R;y\ne x+3\)"

Nếu \(a\ne3\Rightarrow\) tập B có phần tử 3 nhưng tập A ko có \(\Rightarrow A\ne B\) (ko thỏa mãn)
\(\Rightarrow a=3\)
Khi đó \(A=\left\{5;1;3\right\}\) ; \(B=\left\{5;3;b\right\}\)
\(\Rightarrow b=1\)

\(x^2-2x+m=0\Leftrightarrow x^2-2x-3=-m-3\)
Từ đồ thị ta thấy:
a.
Phương trình vô nghiệm khi \(-m-3< -4\Rightarrow m>1\)
b.
Phương trình có nghiệm kép khi \(-m-3=-4\Rightarrow m=1\)
c.
Phương trình có 2 nghiệm pb khi:
\(-m-3>-4\Rightarrow m< 1\)
d.
Phương trình có 2 nghiệm pb thuộc \(\left[-1;3\right]\) khi: \(-4< m\le0\)
e.
Có 2 nghiệm pb ko thuộc \(\left[-1;3\right]\) khi \(m>0\)

\(\Leftrightarrow2mx^2-2mx-x^2+1=0\)
\(\Leftrightarrow2mx\left(x-1\right)-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2mx-x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\\left(2m-1\right)x=1\end{matrix}\right.\)
Pt có nghiệm thuộc khoảng đã cho khi \(\left(2m-1\right)x=1\) có nghiệm thuộc (-1;0)
\(\Rightarrow\left\{{}\begin{matrix}2m-1\ne0\\x=\dfrac{1}{2m-1}\in\left(-1;0\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\-1< \dfrac{1}{2m-1}< 0\end{matrix}\right.\) \(\Rightarrow m< 0\)

\(0< 25^0< 90^0\Rightarrow cos25^0>0\)
\(\Rightarrow cos25^0=\sqrt{1-sin^225^0}=\sqrt{1-a^2}\)
\(tan25^0=\dfrac{sin25^0}{cos25^0}=\dfrac{a}{\sqrt{1-a^2}}\)
\(cot25^0=\dfrac{1}{tan25^0}=\dfrac{\sqrt{1-a^2}}{a}\)

4d.
Để ý rằng tập \(3k+1\), nếu k lẻ hay \(k=2n+1\Rightarrow3k+1=3\left(2n+1\right)+1=6n+4\) chính là tập B
Nếu k chẵn hay \(k=2n\Rightarrow3k+1=6n+1\)
Từ đó ta có \(B\subset A\) nên:
\(A\cap B=B\)
\(A\cup B=A\)
\(A\backslash B=C\) với \(C=\left\{6n+1|n\in Z\right\}\)
\(B\backslash A=\varnothing\)


a.
\(\Leftrightarrow\sqrt{2x^2+5x+3}=-x-3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x-3\ge0\\2x^2+5x+3=\left(-x-3\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-3\\2x^2+5x+3=x^2+6x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-3\\x^2-x-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-3\\\left[{}\begin{matrix}x=3\left(loại\right)\\x=-2\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy pt vô nghiệm
b.
\(\Leftrightarrow\sqrt{2x^2+x+3}=1-x\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-x\ge0\\2x^2+x+3=\left(1-x\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\2x^2+x+3=1-2x+x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\x^2+3x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x=-1\left(loại\right)\\x=-2\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy pt vô nghiệm
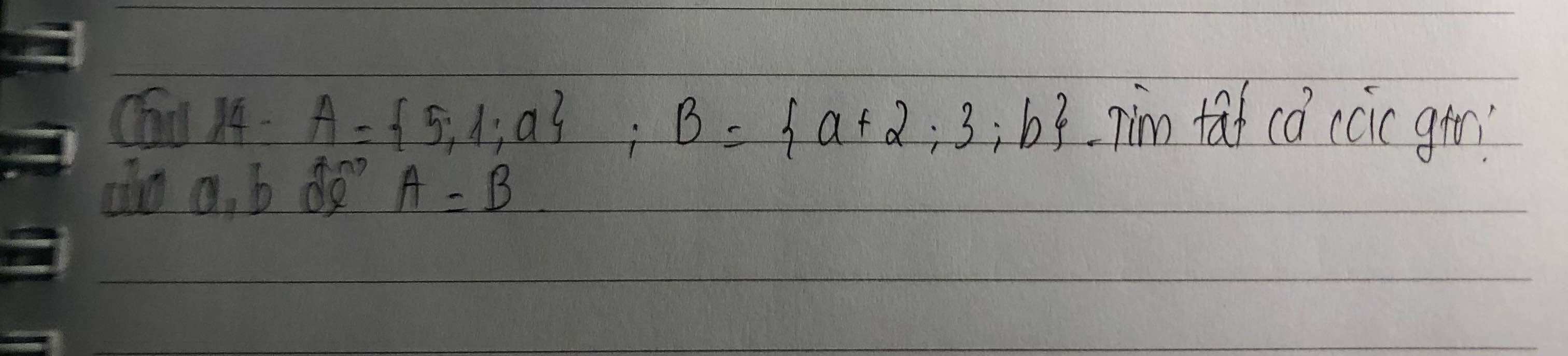


Mình cũng ko biết
`->` Chưa đúng.
`-` Xét:
`+` Hai cặp cạnh đối song song.
`+` Hai cặp cạnh đối bằng nhau.
`+` Hai cặp góc đối bằng nhau.
`+` Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
`+` Một cặp cạnh đối vừa song song vừa bằng nhau.