Cho biểu thức $P=\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{2 \sqrt{x}}{\sqrt{x}-5}-\dfrac{3 x+25}{x-25}$, với $x \geq 0, x \neq 25$.
1. Rút gọn biểu thức $P$.
2. Tìm các giá trị của $x$ để $P=\dfrac{5}{7}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bđt Svácxơ, ta có:
\(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)
\(\dfrac{1}{x+y}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\)
Áp dụng, thay vào A, ta có:
\(A\le\text{Σ}\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\le\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{3}{2}\)
Dấu "="⇔\(a=b=c=1\)

A B x y t z O C D M E F
Ta có
\(\dfrac{OA}{OB}=\dfrac{MC}{MD}=1\) => AC//OM//BD (Talet đảo)
=> ABDC là hình thang
Ta có OA=OB; MC=MD => OM là đường trung bình của hình thang ABDC
\(\Rightarrow OM=\dfrac{AC+BD}{2}\Rightarrow2.OM=AC+BD\)


a) Delta = 4m^2 - 4(2m -1)
= 4m^2 -8m + 4
= (2m)^2 - 2.2m.2 + 2^2
= (2m-2)^2
Delta luôn lớn hơn hoặc bằng 0 với mọi m do đó phương trình luôn có nghiệm với mọi m
b) x1, x2 là nghiệm khi đó ta có x1+x2 = 2m, x1x2 =2m-1
A = x1^2 + x2^2 - 2x1x2
= (x1+x2)^2 - 4x1x2
= (2m)^2 -4(2m-1)
= (2m-2)^2
Ta thấy A nhỏ nhất khi 2m-2 =0 => m= 1

a) \(A=\dfrac{144-\sqrt{144}}{2-\sqrt{144}}=\dfrac{144-12}{2-12}=-13,2\)
b) \(B=\dfrac{x+3}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(P=AB=\dfrac{x-\sqrt{x}}{2-\sqrt{x}}.\dfrac{2-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
c) \(P< \dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}+1}< \dfrac{1}{3}\) (\(x\ge0,x\ne1,x\ne4\))
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\)
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
(đúng do \(x\ne1\))
Bất đẳng thức cuối cùng đúng, mà ta biến đổi tương đương nên bất đẳng thức cần chứng minh đúng.
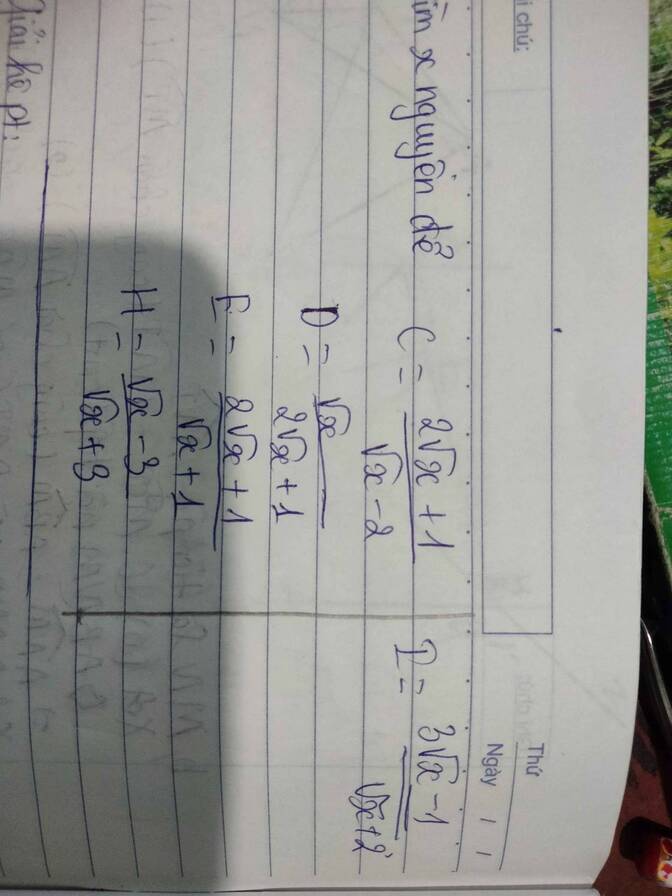 Tìm x để bt nguyê
Tìm x để bt nguyê giúp mình nhâ
giúp mình nhâ