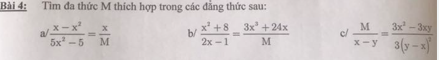 giúp em bài 4 này với ạ,tick ạ
giúp em bài 4 này với ạ,tick ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^4+8x=0\)
=>\(x\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x^3+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(x^4\) + 8\(x\) = 0
\(x^{ }\)(\(x^3\) + 8) = 0
\(\left[{}\begin{matrix}x=0\\x^3+8=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x^3=-8\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-2; 0}

ΔAED vuông tại A
=>\(AE^2+AD^2=ED^2\)
ΔAEB vuông tại A
=>\(AE^2+AB^2=EB^2\)
ΔACD vuông tại A
=>\(AC^2+AD^2=CD^2\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
\(CD^2-CB^2=CA^2+AD^2-CA^2-AB^2=AD^2-AB^2\)
\(ED^2-EB^2=AE^2+AD^2-AE^2-AB^2=AD^2-AB^2\)
Do đó: \(CD^2-CB^2=ED^2-EB^2\)

Gọi vận tốc xe máy là x(km/h)
(Điều kiện: x>28)
Vận tốc của người đi xe đạp là x-28(km/h)
Tổng vận tốc của hai xe là 156:3=52(km/h)
=>x+x-28=52
=>2x=80
=>x=40(nhận)
Vậy: Vận tốc xe máy là 40km/h
Vận tốc của người đi xe đạp là 40-28=12km/h

Gọi vận tốc ban đầu của ô tô là x(km/h)
(Điều kiện: x>0)
Thời gian ô tô đi 180km đầu tiên là: \(\dfrac{180}{x}\left(giờ\right)\)
Độ dài quãng đường còn lại là 400-180=220(km)
Vận tốc của ô tô khi đi trên quãng đường còn lại là:
x+10(km/h)
Thời gian ô tô đi 220km còn lại là \(\dfrac{220}{x+10}\left(giờ\right)\)
Thời gian đi hết quãng đường là 8 giờ nên ta có:
\(\dfrac{180}{x}+\dfrac{220}{x+10}=8\)
=>\(\dfrac{45}{x}+\dfrac{55}{x+10}=2\)
=>\(\dfrac{45x+450+55x}{x\left(x+10\right)}=2\)
=>2x(x+10)=100x+450
=>x(x+10)=50x+225
=>\(x^2-40x-225=0\)
=>(x-45)(x+5)=0
=>\(\left[{}\begin{matrix}x=45\left(nhận\right)\\x=-5\left(loại\right)\end{matrix}\right.\)
Vậy: vận tốc ban đầu của ô tô là 45km/h
Giải:
Gọi vận tốc ban đầu của ô tô là: \(x\) (km/h) ; \(x\) > 0
Vận tốc lúc sau của ô tô là: \(x+10\) (km/h)
Thời gian ô tô đi lúc đầu là: 180 : \(x\) (giờ)
Thời gian ô tô đi lúc sau là: (400 - 180) : (\(x+10\)) = \(\dfrac{220}{x+10}\)
Theo bài ra ta có phương trình:
\(\dfrac{180}{x}\) + \(\dfrac{220}{x+10}\) = 8
\(\dfrac{45}{x}\) + \(\dfrac{55}{x+10}\) = 2
45(\(x+10\)) + 55\(x\) = 2.\(x\) (\(x+10\))
45\(x\) + 450 + 55\(x\) = 2\(x^2\) + 20\(x\)
2\(x^2\) + 20\(x\) - 55\(x\) - 45\(x\) = 450
2\(x^2\) + (20\(x\) - 55\(x\) - 45\(x\)) = 450
2\(x^2\) + (- 35\(x\) - 45\(x\)) = 450
2\(x^2\) - 80\(x\) = 450
\(x^2\) - 40\(x\) = 225
\(x^2\) - 40\(x\) + 400 = 625
(\(x-20\))2 = 252
\(\left[{}\begin{matrix}x-20=25\\x-20=-25\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=25+20\\x=-25+20\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=45\\x=-5\end{matrix}\right.\)
\(x=-5\) < 0 (loại)
Vậy \(x=45\)
Kết luận:...


1)
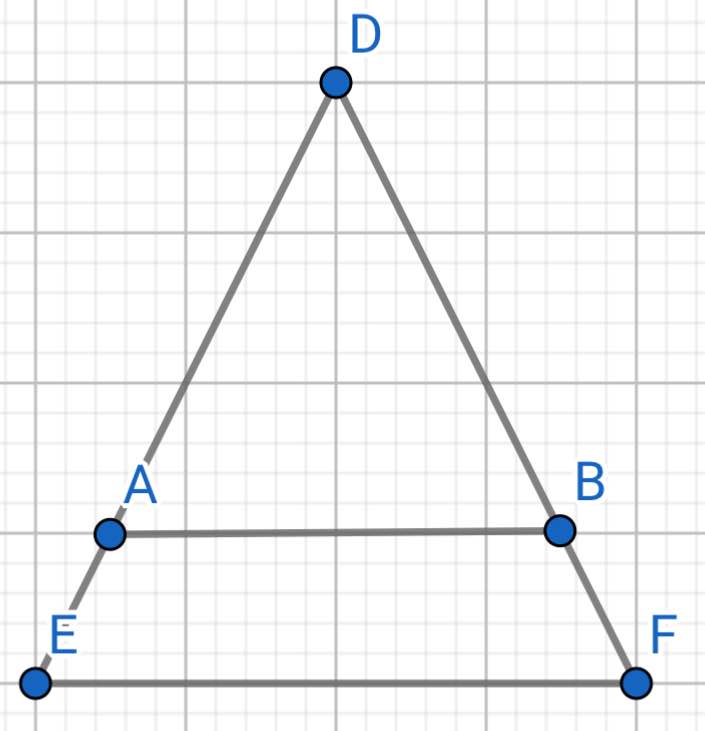
a) Do tam giác DEF cân tại D (gt)
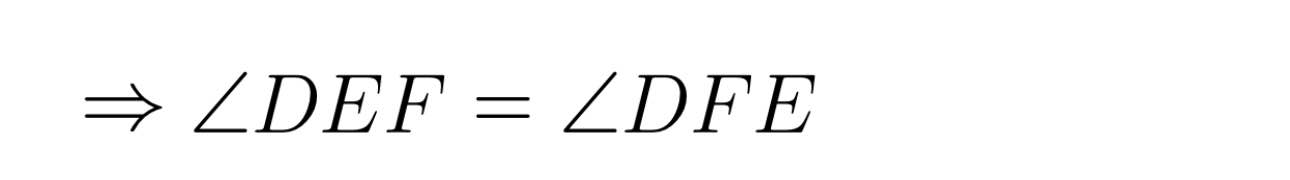
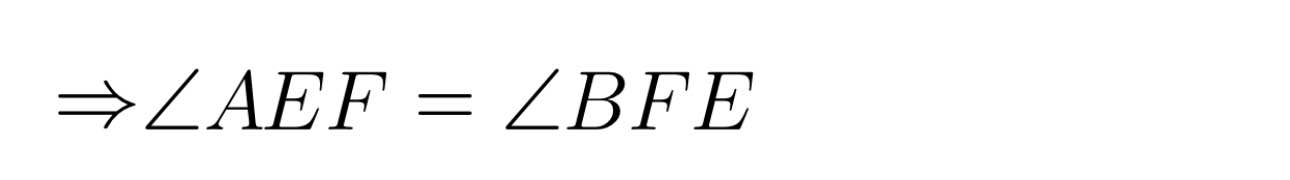
Tam giác DAB có:
DA = DB (gt)
=> Tam giác DAB cân tại D
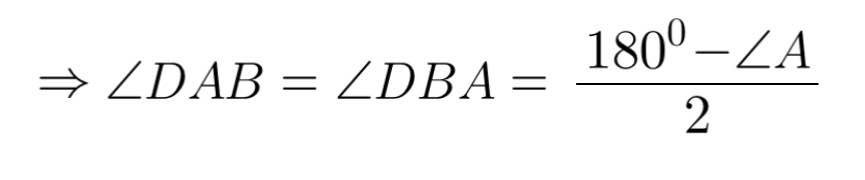
Do tam giác DEF cân tại D (gt)
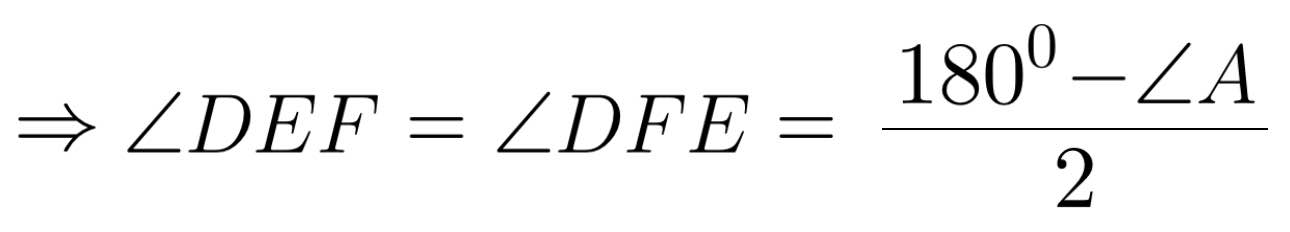
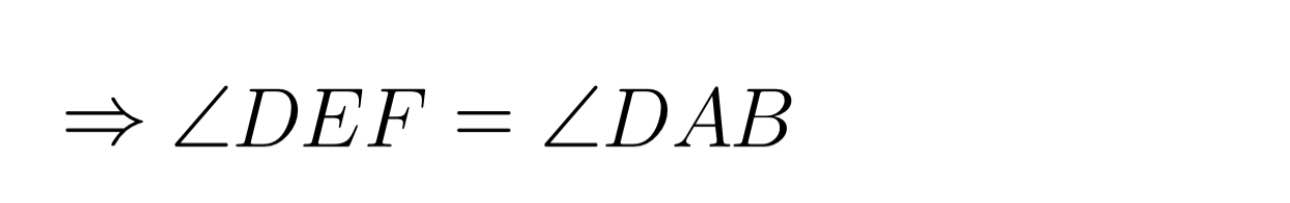
Mà góc DEF và góc DAB đồng vị

=> EABF là hình thang
Mà:
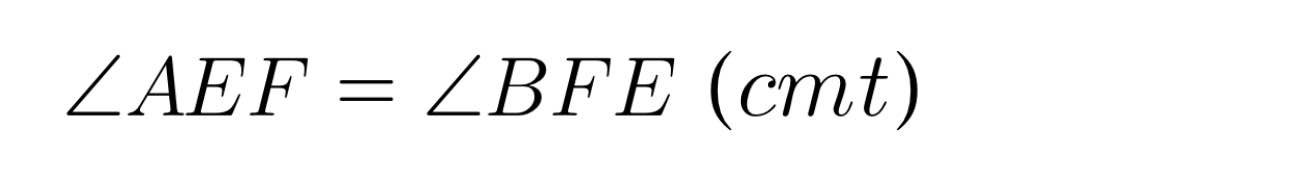
=> EABF là hình thang cân
b) Do tam giác DEF cân tại D (gt)
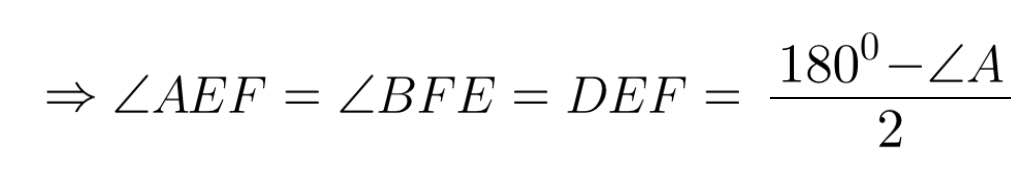
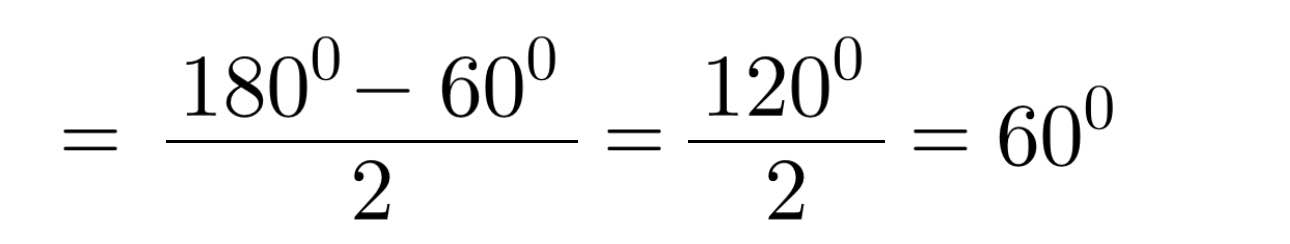
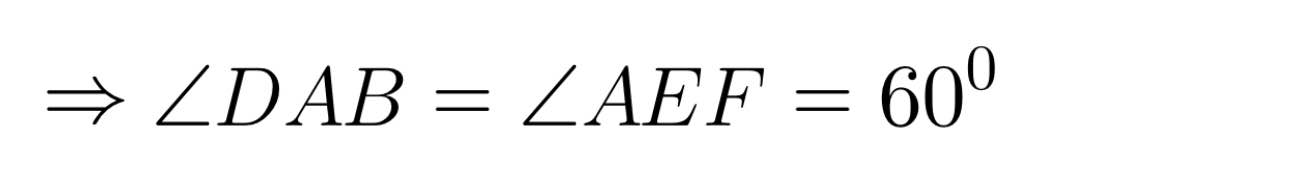
Ta có:
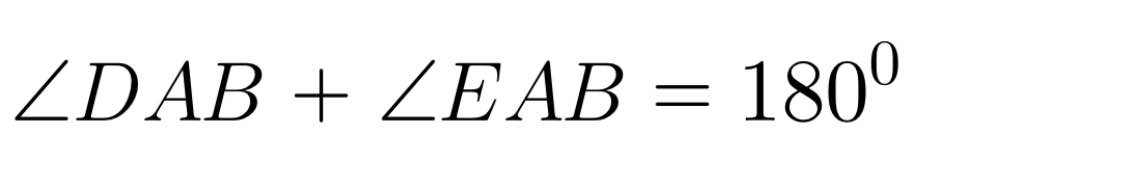
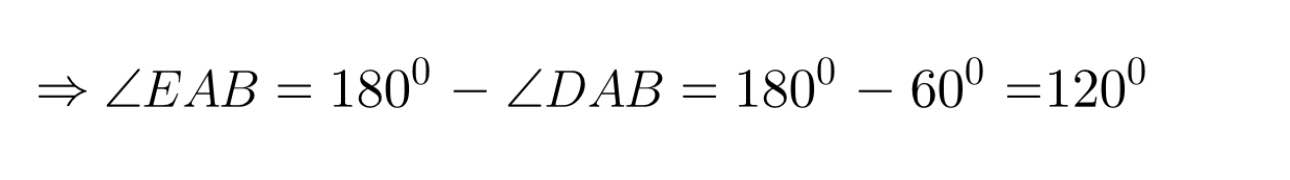

Bài 3
Tam giác ABD có:
AB = AD (gt)
=> Tam giác ABD cân tại A
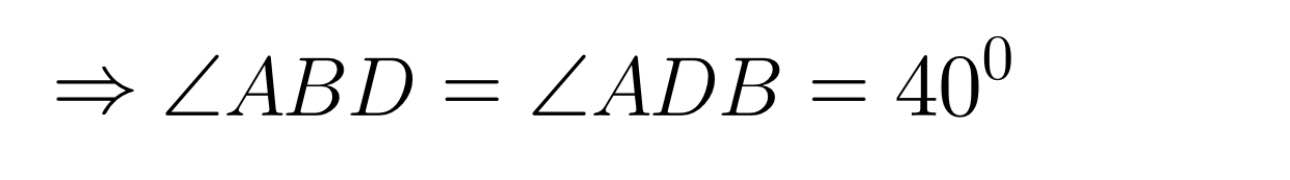
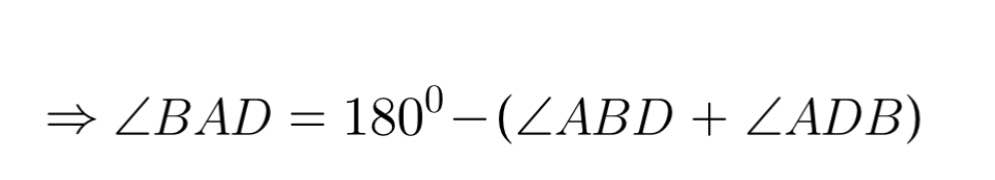
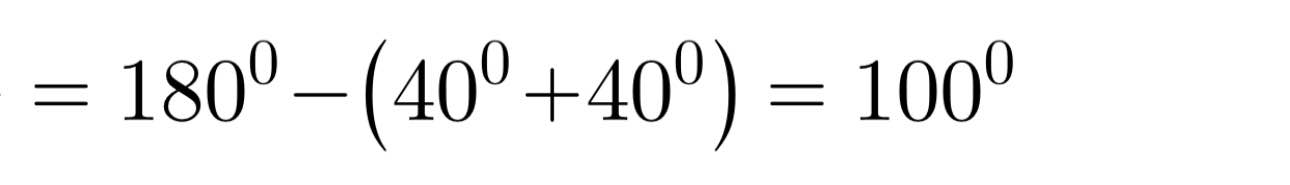
Ta có:
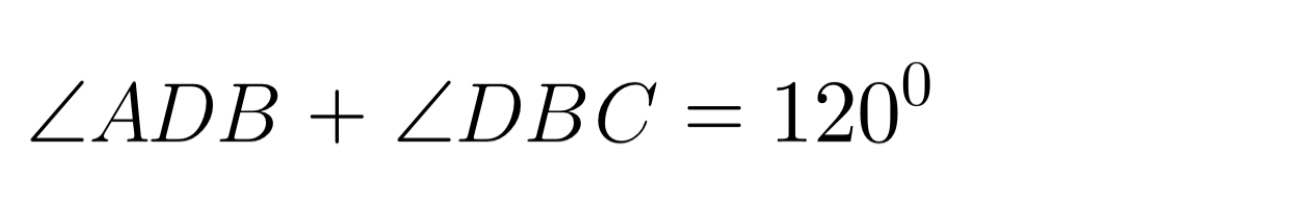
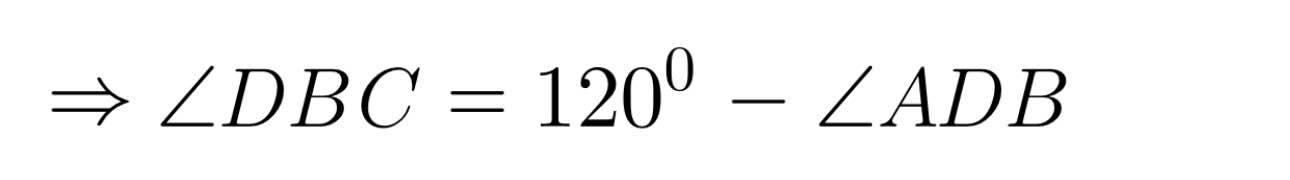
= 120⁰ − 40⁰
= 80⁰
Tam giác BCD có:
CB = CD (gt)
=> Tam giác BCD cân tại C
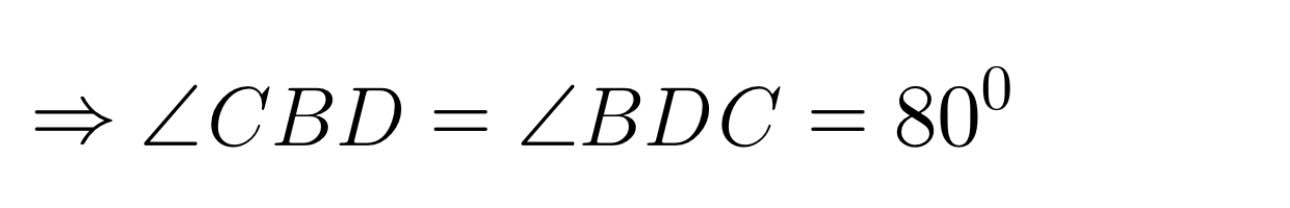
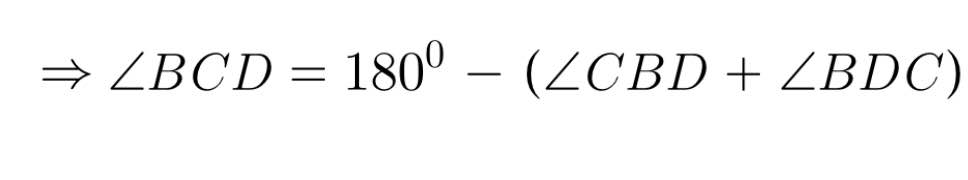
= 180⁰ − (80⁰ + 80⁰) = 20⁰
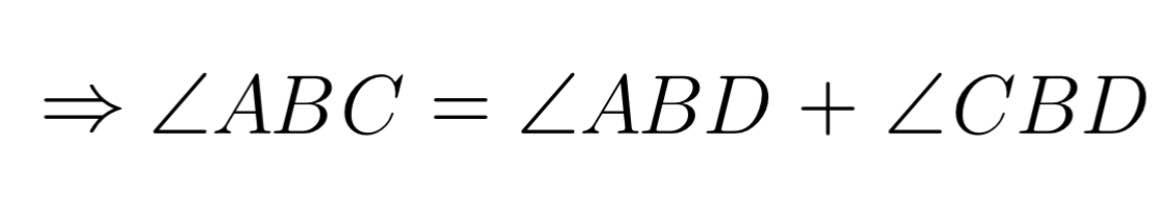
= 40⁰ + 40⁰
= 80⁰

\(\Leftrightarrow x^2+2y^2+3xy-4x-5y+3=4\)
\(\Leftrightarrow\left(x^2+2xy-3x\right)+\left(xy+2y^2-3y\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow x\left(x+2y-3\right)+y\left(x+2y-3\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow\left(x+2y-3\right)\left(x+y-1\right)=4\)
Ta có bảng:
| x+2y-3 | -4 | -2 | -1 | 1 | 2 | 4 |
| x+y-1 | -1 | -2 | -4 | 4 | 2 | 1 |
| x | 1 | -3 | -8 | 6 | 1 | -3 |
| y | -1 | 2 | 5 | -1 | 2 | 5 |
Vậy \(\left(x;y\right)=\left(1;-1\right);\left(-3;2\right);\left(-8;5\right);\left(6;-1\right);\left(1;2\right);\left(-3;5\right)\)

\(D=\dfrac{2^2-1}{2^2}+\dfrac{3^2-1}{3^2}+...+\dfrac{2025^2-1}{2025^2}\)
\(=\left(\dfrac{2^2}{2^2}+\dfrac{3^2}{3^2}+...+\dfrac{2025^2}{2025^2}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=\left(1+1+...+1\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=2024-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+....+\dfrac{1}{2025^2}\right)\)
Đặt \(E=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\)
Do \(E>0\Rightarrow D< 2024\) (1)
Lại có:
\(E< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2024.2025}\)
\(E< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2024}-\dfrac{1}{2025}\)
\(E< 1-\dfrac{1}{2025}< 1\)
\(\Rightarrow D-E>2024-1=2023\) (2)
(1);(2) \(\Rightarrow2023< D< 2024\)
\(\Rightarrow D\) nằm giữa 2 số tự nhiên liên tiếp nên D ko thể là số tự nhiên

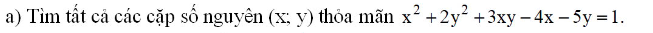

a: \(\dfrac{x-x^2}{5x^2-5}=\dfrac{x}{M}\)
=>\(M=\dfrac{x\left(5x^2-5\right)}{-x^2+x}=\dfrac{5x\left(x-1\right)\left(x+1\right)}{-x\left(x-1\right)}=-5\left(x+1\right)\)
=>M=-5x-5
b: \(\dfrac{x^2+8}{2x-1}=\dfrac{3x^3+24x}{M}\)
=>\(M=\dfrac{\left(2x-1\right)\left(3x^3+24x\right)}{x^2+8}=\dfrac{\left(2x-1\right)\cdot3x\left(x^2+8\right)}{\left(x^2+8\right)}\)
=>\(M=3x\left(2x-1\right)=6x^2-3x\)
c: \(\dfrac{M}{x-y}=\dfrac{3x^2-3xy}{3\left(y-x\right)^2}\)
=>\(\dfrac{M}{x-y}=\dfrac{3x\left(x-y\right)}{3\left(x-y\right)^2}=\dfrac{x}{x-y}\)
=>M=x