Giải hệ phương trình:
$\left\{\begin{array}{l}
4 x+3 y=11 \\
4 x-y=7
\end{array}\right. \text {. }$
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


thay x=1 và y=5 vào y=(2m+1)x+m
=> 5=(2m+1).1+m
<=> 5= 2m+1+m
<=> 5=3m+1
<=>3m= 4
<=>m=4/3
vạy m= 4/3

Áp dụng bđt Svácxơ, ta có:
\(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\)
\(\dfrac{1}{x+y}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\)
Áp dụng, thay vào A, ta có:
\(A\le\text{Σ}\dfrac{1}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
\(\le\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{3}{2}\)
Dấu "="⇔\(a=b=c=1\)

A B x y t z O C D M E F
Ta có
\(\dfrac{OA}{OB}=\dfrac{MC}{MD}=1\) => AC//OM//BD (Talet đảo)
=> ABDC là hình thang
Ta có OA=OB; MC=MD => OM là đường trung bình của hình thang ABDC
\(\Rightarrow OM=\dfrac{AC+BD}{2}\Rightarrow2.OM=AC+BD\)


a) Delta = 4m^2 - 4(2m -1)
= 4m^2 -8m + 4
= (2m)^2 - 2.2m.2 + 2^2
= (2m-2)^2
Delta luôn lớn hơn hoặc bằng 0 với mọi m do đó phương trình luôn có nghiệm với mọi m
b) x1, x2 là nghiệm khi đó ta có x1+x2 = 2m, x1x2 =2m-1
A = x1^2 + x2^2 - 2x1x2
= (x1+x2)^2 - 4x1x2
= (2m)^2 -4(2m-1)
= (2m-2)^2
Ta thấy A nhỏ nhất khi 2m-2 =0 => m= 1
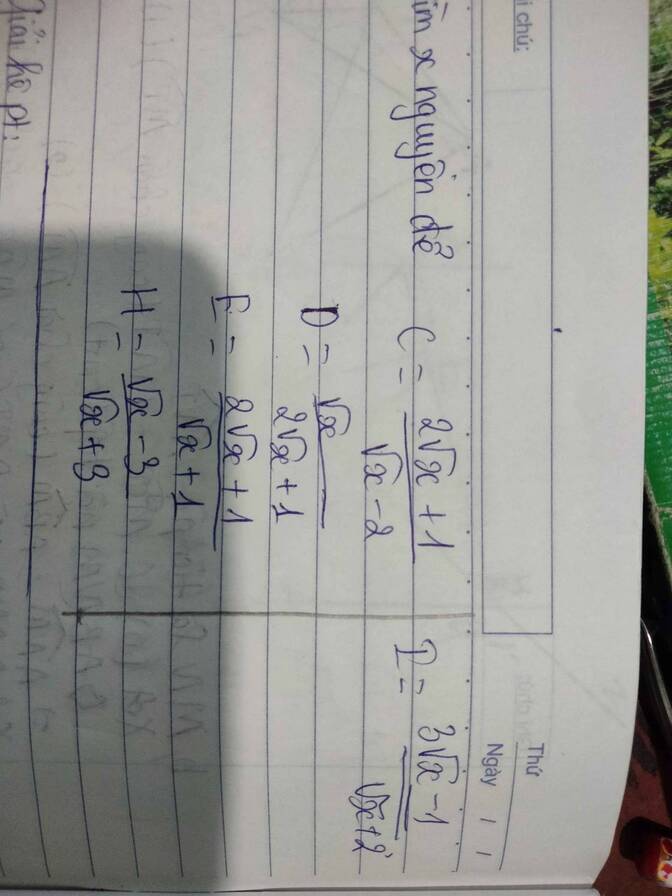 Tìm x để bt nguyê
Tìm x để bt nguyê giúp mình nhâ
giúp mình nhâ
<=>\(\left\{{}\begin{matrix}4x+3y=11\\4x-y=7\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}4y=4\\4x-y=7\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}y=1\\4x-1=7\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}y=1\\4x=8\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
vậy hệ đã cho có nghiệm (x;y) = (2;1)