so sánh 3/-8 và 5/8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
2,5dm = 25cm
Diện tích toàn phần của hình hộp chữ nhật là:
(36 + 19) x 2 x 25 = 2750 \(\operatorname{cm}^2\)
Đáp số: 2750\(\operatorname{cm}^2\)
2,5dm=25cm
Diện tích xung quanh là:
\(\left(36+19\right)\times2\times25=50\times55=2750\left(cm^2\right)\)
Diện tích toàn phần là:
\(2750+2\times36\times19=4118\left(cm^2\right)\)


A = 23 x 24 x 25 x 26 x 27 x 28 x 29
Vì thừa số có tận cùng bằng 5 nhân với bất cứ thừa số chẵn nào cũng có tích tận cùng là 0
Tích trên có thừa số 25 và 24
Vậy A có tận cùng là 0

Vì 2022<2023<2024<2025
nên \(\dfrac{1}{2022}>\dfrac{1}{2023}>\dfrac{1}{2024}>\dfrac{1}{2025}\)
=>PHân số nhỏ nhất là \(\dfrac{1}{2025}\)

Đây là toán nâng cao chuyên đề toán hai đại lượng tỉ lệ thuận, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Thời gian làm 4 cái ghế bằng thời gian làm:
1 x 2 = 2 (cái bàn)
Thời gian làm 1 cái bàn và 4 cái ghế bằng thời gian làm:
1 + 2 = 3 (cái bàn)
Thời gian làm 1 cái bàn là:
22 giờ 30 phút : 3 = 7 giờ 30 phút
Thời gian làm một cái ghế là:
7 giờ 30 phút : 2 = 3 giờ 45 phút
Đáp số: làm một cái ghế hết thời gian là 3 giờ 45 phút.

Để cộng hai phân số \(\frac{2}{3}\) và \(\frac{4}{5}\), ta cần tìm mẫu số chung. Mẫu số chung nhỏ nhất của 3 và 5 là 15.
Bước 1: Quy đồng mẫu số cho cả hai phân số:
\(\frac{2}{3} = \frac{2 \times 5}{3 \times 5} = \frac{10}{15}\)\(\frac{4}{5} = \frac{4 \times 3}{5 \times 3} = \frac{12}{15}\)Bước 2: Cộng hai phân số:
\(\frac{10}{15} + \frac{12}{15} = \frac{10 + 12}{15} = \frac{22}{15}\)Vậy \(\frac{2}{3} + \frac{4}{5} = \frac{22}{15}\), hay có thể viết dưới dạng hỗn số \(1 \frac{7}{15}\).

Đây là toán nâng cao chuyên đề phép chia có dư, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng tư duy logic như sau:
Giải:
Vì số đó chia cho 8 dư 3 nên số đó sẽ chia hết cho 8 khi thêm vào số đó là:
8 - 3 = 5(đơn vị)
Vì 8 chia hết cho 4 nên số đó khi thêm vào 5 đơn vị thì chia hết cho 8 cũng chia hết cho 4.
mà 5 chia 4 dư 1, vậy số đó ban đầu chia 4 có số dư là:
4 - 1 = 3 (đơn vị)
Số cần tìm là:
77848 x 4 + 3 = 311395
Đáp số: 311395

Giải:
Diện tích tam giác là:
5 x 6 : 2 = 15(cm\(^2\))
Đáp số: 15cm\(^2\)
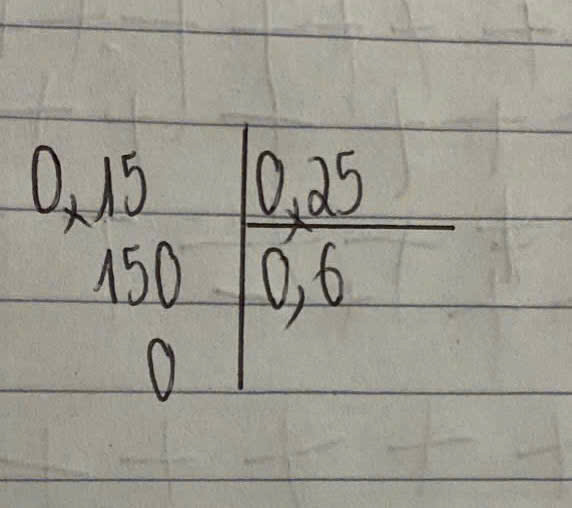
\(\frac{3}{-8}\) < 0 < \(\frac58\)
Vậy \(\frac{3}{-8}\) < \(\frac58\)
\(\dfrac{3}{-8}< 0;0< \dfrac{5}{8}\)
Do đó: \(\dfrac{3}{-8}< \dfrac{5}{8}\)