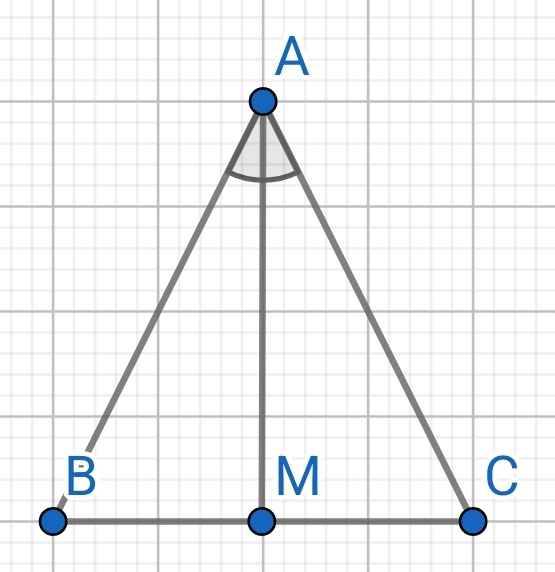
Vì AB=AC=> Tam giác ABC cân tại A

+) Tam giác ABC cân tại A có AM là tpg góc BAC

=> AM đồng thời là đường cao và đường trung tuyến

a) Do AM là đường trung tuyến 

=> M là trung điểm BC

b) Do AM là đường cao

=> AM\(\perp\)BC

 a) Do AM là tia phân giác của ∠BAC (gt)

⇒ ∠BAM = ∠CAM

Xét ∆ABM và ∆ACM có:

AM là cạnh chung

∠BAM = ∠CAM (cmt)

AB = AC (gt)

⇒ ∆ABM = ∆ACM (c-g-c)

⇒ BM = CM (hai cạnh tương ứng)

⇒ M là trung điểm của BC

b) Do ∆ABM = ∆ACM (cmt)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180⁰ (kề bù)

⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BC

81 = x³

x = ∛81

x = 3∛3

5ˣ⁺² - 5ˣ = 20

5ˣ(5² - 1) = 20

5ˣ.24 = 20

5ˣ = 20/24

5ˣ = 5/6

Em xem lại đề nhé!

\(3.\left(x-\dfrac{1}{2}\right)^3=81\\ =>\left(x-\dfrac{1}{2}\right)^3=81:3=27\\ =>x-\dfrac{1}{2}=3\\ =>x=3+\dfrac{1}{2}=\dfrac{7}{2}\)

3.(x - 1/2)³ = 81

(x - 1/2)³ = 81 : 3

(x - 1/2)³ = 27

(x - 1/2)³ = 3³

x - 1/2 = 3

x = 3 + 1/2

x = 7/2

\(\dfrac{16}{2^x}=2\)\(\Rightarrow16:2=2^x\Rightarrow8=2^x\Rightarrow2^3=2^x\Rightarrow x=3\)

Trời oi

giúp mik với

\(\dfrac{2}{14}\) + \(\dfrac{6}{15}\)

= \(\dfrac{1}{7}\) + \(\dfrac{2}{5}\)

= \(\dfrac{5}{35}\) + \(\dfrac{14}{35}\)

= \(\dfrac{19}{35}\)

1

Ghi rõ cách làm nhé bạn