với các số thực a,b,c thỏa mãn -1≤a,b,c≤1 và a+b+c=0, tìm giá trị lớn nhất của biểu thức P=a2021+b2022+c2023
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x+\sqrt{11}}{x^2+2x\sqrt{11}+11}\) = \(\dfrac{x+\sqrt{11}}{(x+\sqrt{11)}^2}\) = x +\(\sqrt{11}\)
x+√11x2+2x√11+11x+11x2+2x11+11 = x+√11(x+√11)2x+11(x+11)2 = x +√11

\(\dfrac{x^2-3}{x-\sqrt{3}}\) = \(\dfrac{x^2-\sqrt{3^2}}{x-\sqrt{3}}\) = \(\dfrac{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)}{x-\sqrt{3}}\) = x +\(\sqrt{3}\)

14 balls are not blue. => yellow + red + pink = 14
16 balls are not yellow. => blue + red + pink = 16
24 balls are not red. => blue + yellow + pink = 24
12 balls are not pink. => blue + yellow + red = 12
====> 3 yellow + 3 red + 3 blue + 3 pink = 14+16+24+12
3(yellow + red + blue + pink) = 66
yellow + red + blue + pink = 66:3 =22

b) xy(x2 + y2) + 2 = (x + y)2
<=> xy(x2 + y2 + 2xy) - 2(xy)2 + 2 = (x + y)2
<=> (x + y)2(xy - 1) - 2(xy - 1)(xy + 1) = 0
<=> (xy - 1)[(x + y)2 - 2xy - 2] = 0
<=> (xy - 1)(x2 + y2 - 2) = 0
<=> \(\left[{}\begin{matrix}xy=1\\x^2+y^2=2\end{matrix}\right.\)
Với xy = 1
5x2y - 4xy2 + 3y3 - 2(x + y) = 0
<=> xy(5x - 4y) + 3y3 - 2x - 2y = 0
<=> 3x - 6y + 3y3 = 0
<=> x = 2y - y3 (1)
Thay (1) vào xy = 1
<=> (2y - y3)y = 1
<=> y4 - 2y2 + 1 = 0
<=> (y2 - 1)2 = 0
<=> y = \(\pm1\)
Với y = 1 => x = 1
y = -1 => x = -1
Khi x2 + y2 = 2
<=> x2 = 2 - y2 ; y2 = 2 - x2
khi đó 5x2y - 4xy2 + 3y3 - 2(x + y) = 0
<=> 5y(2 - y2) - 4x(2 - x2) + 3y3 - 2x - 2y = 0
<=> -2y3 + 8y - 10x + 4x3 = 0
<=> - y3 + 4y - 5x + 2x3 = 0
<=> x3 - y3 - 4(x - y) + x3 - x = 0
<=> (x - y)(x2 - xy + y2) - 4(x - y) + x3 - x = 0
<=> (x - y)(2 - xy) + x(x2 - 1) - 4(x - y) = 0
<=> (x - y)(-2 - xy) + x(-y2 + 1) = 0
<=> -2x - x2y + 2y + xy2 - xy2 + x = 0
<=> -x - x2y + 2y = 0
<=> -x - x2y + (x2 + y2)y = 0
<=> y3 = x
Khi đó x2 + y2 = 2
<=> y6 + y2 = 2
<=> y6 + y2 - 2 = 0
<=> (y6 - 1) + (y2 - 1) = 0
<=> (y - 1)(y + 1)(y4 + y2 + 1) + (y - 1)(y + 1) = 0
<=> (y - 1)(y + 1)(y4 + y2 + 2) = 0
<=> \(\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\)(vì y4 + y2 + 2 > 0)
Với y = 1 => x = 1
Với y = -1 => x = -1
Vậy (x;y) = (1 ; 1) ; (-1 ; -1)
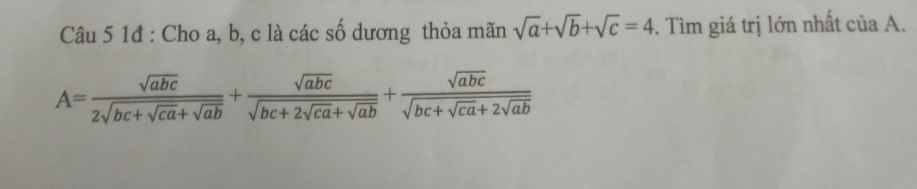
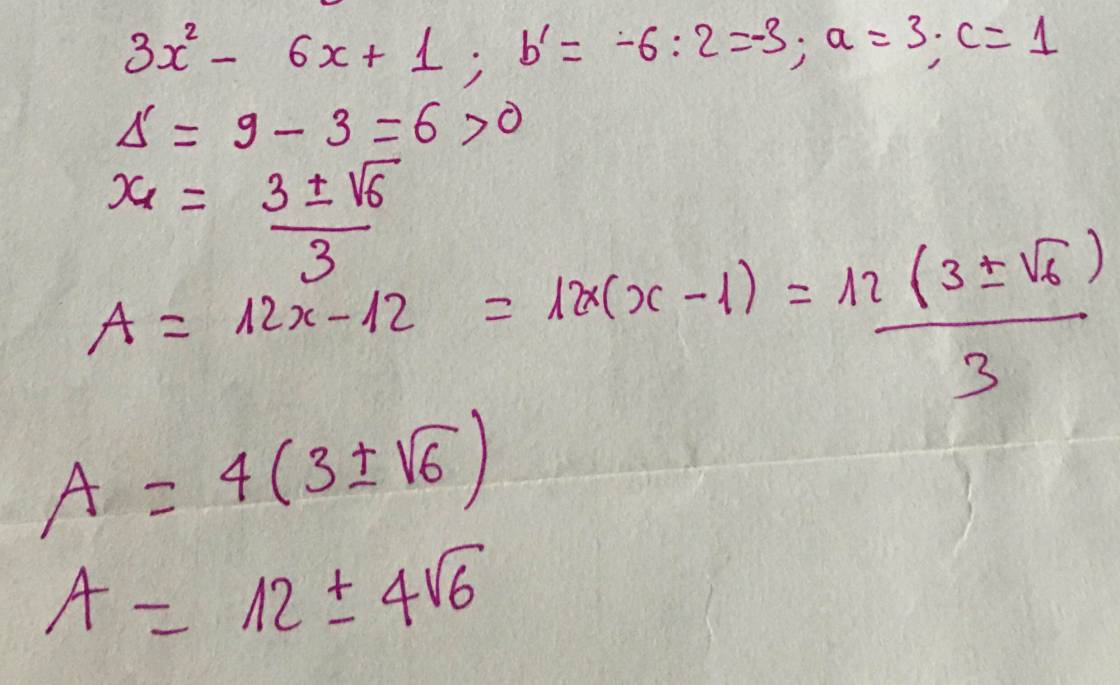

tập hợp tất cả các giá trị của tham số m để hàm số y=x2-2mx+3 trên đoạn (1, +∞)
tập hợp tất cả các giá trị của tham số m để hàm số y=x2-2mx++m2+4 đồng biến trên khoảng (1, +∞)