2023 + 4 mũ x - 4 =2027
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau:
Giải:
3\(^{x+1}\) = 4\(^{x-1}\)
Vì 3 là số lẻ nên 3\(^{x-1}\) là số lẻ \(\forall\) \(x\) \(\in\) N; ⇒ 4\(x-1\) là số lẻ
⇒ 4\(^{x-1}\) = 1 ⇒ 4\(x-1\) = 40 ⇒ \(x-1\) = 0⇒ \(x=1\)
Với \(x\) = 1 ta có: 31+1 = 41-1 ⇒ 32 = 40 ⇒ 9 = 1 (vô lý)
Vậy \(x\) = 1 loại
Kết luận không có giá trị nào của \(x\) là số tự nhiên thỏa mãn đề bài.

Hình lăng trụ tứ giác đều là hình đa diện có hai mặt đáy là hai hình vuông bằng nhau và hai mặt đáy nằm trên hai mặt phẳng song song, các mặt bên là các hình chữ nhật. Tất cả các mặt bên đều song song và bằng nhau đồng thời vuông góc với mặt đáy.

C = \(\dfrac{x+4}{x-1}\) (\(x\) ≠ 1) ⇒ C = 1 + \(\dfrac{5}{x-1}\)
C nguyên Dương khi và chỉ khi: 5 ⋮ \(x-1\) và \(\dfrac{x+4}{x-1}\) > 0
5 ⋮ \(x\) - 1 ⇒ \(x-1\) \(\in\) Ư(5) = {-5; -1; 1; 5}
Lập bảng ta có:
| \(x-1\) | -5 | -1 | 1 | 5 |
| \(x\) | -4 | 0 | 2 | 6 |
| C = \(\dfrac{x+4}{x-1}\) | 0 | -4 | 6 | 2 |
| C > 0 | loại | loại | nhận | nhận |
Theo bảng trên ta có các giá trị nguyên dương của C là: 6; 2
Kết luận các giá trị nguyên dương của C là 6 và 2

2\(\dfrac{4}{5}\) + (- \(\dfrac{3}{7}\) + \(\dfrac{2}{3}\)) : - \(\dfrac{5}{14}\)
= \(\dfrac{14}{5}\) + (\(\dfrac{-9}{21}\) + \(\dfrac{14}{21}\)) : - \(\dfrac{5}{14}\)
= \(\dfrac{14}{5}\) + \(\dfrac{5}{21}\) x (- \(\dfrac{14}{5}\))
= \(\dfrac{14}{5}\) - \(\dfrac{2}{3}\)
= \(\dfrac{42}{15}\) - \(\dfrac{10}{15}\)
= \(\dfrac{32}{15}\)

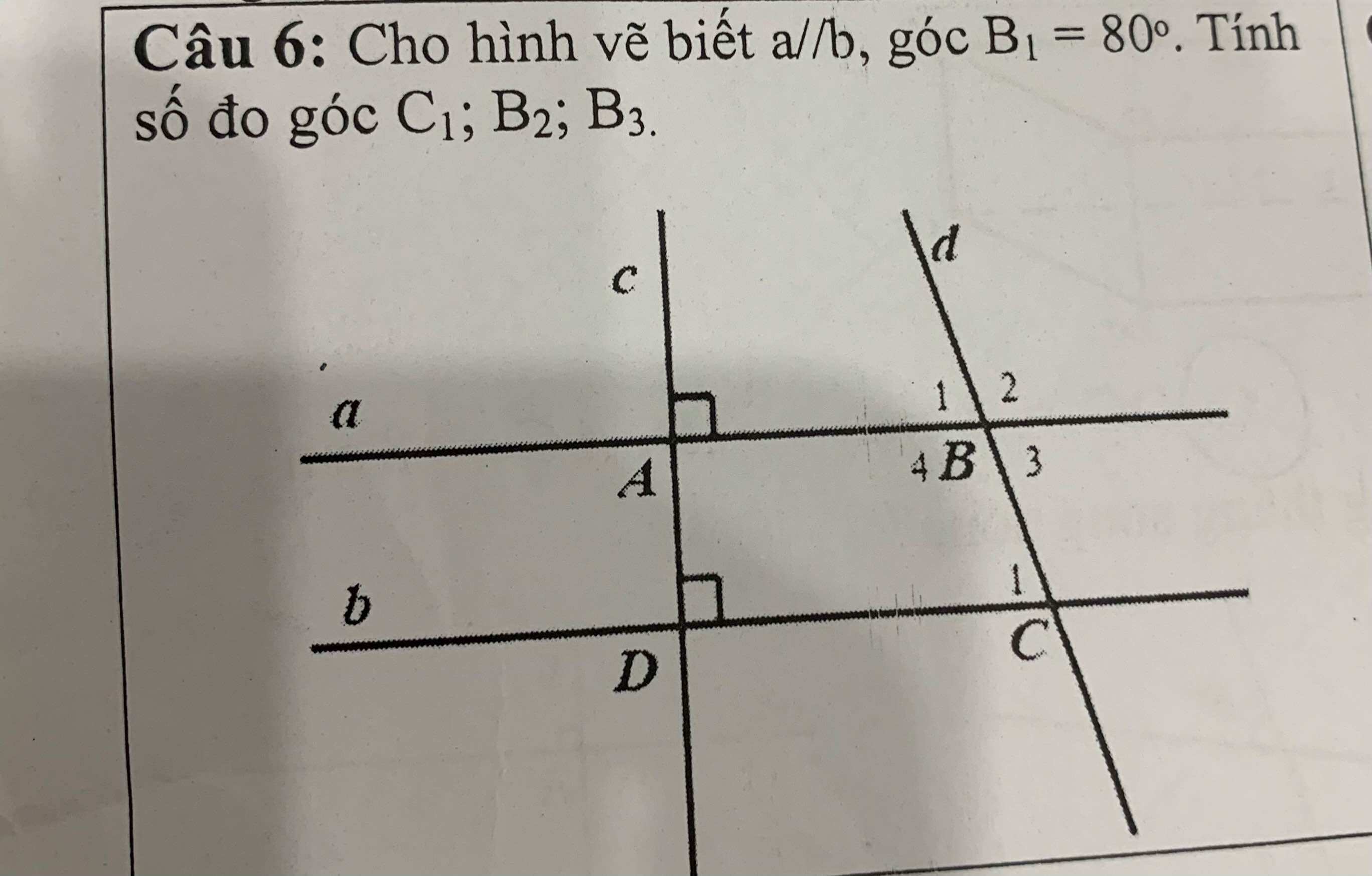
Ta có: \(\widehat{B_1}=\widehat{B_3}\)(hai góc đối đỉnh)
mà \(\widehat{B_1}=80^0\)
nên \(\widehat{B_3}=80^0\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)
=>\(\widehat{B_2}=180^0-80^0=100^0\)
Ta có: a//b
=>\(\widehat{C_1}=\widehat{B_3}\)(hai góc so le trong)
=>\(\widehat{C_1}=80^0\)

- \(\dfrac{11}{24}\) : \(\dfrac{17}{23}\) - \(\dfrac{11}{24}\) : \(\dfrac{17}{11}\) - \(\dfrac{1}{2}\)
= - \(\dfrac{11}{24}\) x \(\dfrac{23}{17}\) - \(\dfrac{11}{24}\) x \(\dfrac{11}{17}\) - \(\dfrac{1}{2}\)
= - \(\dfrac{11}{24}\) x (\(\dfrac{23}{17}\) + \(\dfrac{11}{17}\)) - \(\dfrac{1}{2}\)
= - \(\dfrac{11}{24}\) x 2 - \(\dfrac{1}{2}\)
= - \(\dfrac{11}{12}\) - \(\dfrac{1}{2}\)
= - \(\dfrac{11}{12}\) - \(\dfrac{6}{12}\)
= - \(\dfrac{17}{12}\)

Hãy giải quyết điều này từng bước:
Đầu tiên, chuyển đổi mọi thứ thành một dạng phân số phổ biến:
1/5
vẫn như cũ.
0.125
có thể được chuyển đổi thành
1/8.
5/4 vẫn như cũ.
Vì vậy, ta có:
1/5 −1/8 − 5/4
Bây giờ, tìm một mẫu số chung. Mẫu số chung của 5, 8 và 4 là 40:
1/5 = 8/40; 1/8 = 5/40; 5/4 = 50/40
Bây giờ chúng ta có thể viết lại biểu thức với các phân số tương đương sau:
8/40 − 5/40 − 50/40
Kết hợp các phân số:
(8−5−50)/40=−47/40
Vì vậy, kết quả là:
−47/40
hoặc, ở dạng thập phân.

A B C D E M N
Xét tư giác BCDE có
AD=AB (gt); AE=AC (gt) => BCDE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> DE//BC (cạnh đối hbh) => DN//BM
Mà BM=DN (gt)
=> BMDN là hbh (Tứ giác có 1 cawoj cạnh đối // và bằng nhau là hbh)
Nối MN cắt BD tại A' => A'D=A'B (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Mà AD=AB (gt); \(A\in BD;A'\in BD\)
\(\Rightarrow A'\equiv A\) hay A; M; N thẳng hàng
Ta có BMDN là hbh (cmt) => AM=AN (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Xét tg vuông ABC nếu
\(BM=CN\Rightarrow AM=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Mà AM=AN (cmt)
\(\Rightarrow MN=AM+AN=\dfrac{BC}{2}+\dfrac{BC}{2}=BC\)
vì 2023+4x = 2027 => 4x = 2027 - 2023 => 4x = 4 => x = 1
2023 + 4\(^{x-4}\) = 2027
4\(^{x-4}\) = 2027 - 2023
4\(^{x-4}\) = 4
4\(^{x-4}\) = 41
\(x-4\) = 1
\(x=1+4\)
\(x=5\)
Vậy \(x=5\)