Mình chỉ cần đáp án thôi nhé!!mik cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 32+(x-48)=84
=>\(x-48=84-32=52\)
=>\(x=52+48=100\)
b: \(\left(x+7\right):3=27\)
=>\(x+7=27\cdot3=81\)
=>x=81-7=74
c: \(39-\left(x-3\right)=14\)
=>x-3=39-14=25
=>x=25+3=28
d: \(23-2\left(x+2\right)=7\)
=>\(2\left(x+2\right)=23-7=16\)
=>x+2=16/2=8
=>x=8-2=6
e: \(\left(40-2x\right):4=3\)
=>\(40-2x=3\cdot4=12\)
=>2x=40-12=28
=>x=28/2=14
f: 25+(42-x)=65
=>42-x=65-25=40
=>x=42-40=2
g: 2x-15=17
=>2x=15+17=32
=>\(x=\dfrac{32}{2}=16\)
h: \(121+\left(518-x\right)=316\)
=>\(518-x=316-121=195\)
=>x=518-195=323
i: \(2x-138=8\cdot9\)
=>2x-138=72
=>2x=72+138=210
=>x=210/2=105
j: \(2\cdot\left(x-1\right)+21=331\)
=>\(2\left(x-1\right)=331-21=310\)
=>x-1=310/2=155
=>x=155+1=156

xx'//yy'
=>\(\widehat{xAB}+\widehat{yBz}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{yBz}+70^0=180^0\)
=>\(\widehat{yBz}=110^0\)
xx'//yy'
=>\(\widehat{xAB}=\widehat{yBz'}\)(hai góc đồng vị)
=>\(\widehat{yBz'}=70^0\)

bài 2:
a: \(\dfrac{1}{9}-0,3\cdot\dfrac{5}{9}+\dfrac{1}{3}\)
\(=\dfrac{1}{9}-\dfrac{3}{10}\cdot\dfrac{5}{9}+\dfrac{1}{3}\)
\(=\dfrac{1}{9}-\dfrac{1}{6}+\dfrac{1}{3}=\dfrac{2}{18}-\dfrac{3}{18}+\dfrac{6}{18}=\dfrac{5}{18}\)
b: \(\left(-\dfrac{2}{3}\right)^2+\dfrac{1}{6}-\left(-0,5\right)^3\)
\(=\dfrac{4}{9}+\dfrac{1}{6}-\left(-\dfrac{1}{2}\right)^3\)
\(=\dfrac{8}{18}+\dfrac{3}{18}-\dfrac{-1}{8}=\dfrac{11}{18}+\dfrac{1}{8}=\dfrac{44}{72}+\dfrac{9}{72}=\dfrac{53}{72}\)
c: \(0,3-\dfrac{8}{3}:\dfrac{4}{3}\cdot\dfrac{1}{5}+1\)
\(=1,3-\dfrac{8}{3}\cdot\dfrac{3}{4}\cdot\dfrac{1}{5}=1,3-\dfrac{2}{5}=1,3-0,4=0,9=\dfrac{9}{10}\)
d: \(-\dfrac{2}{3}-4\cdot\left(\dfrac{1}{2}+\dfrac{3}{4}\right)^2\)
\(=-\dfrac{2}{3}-4\cdot\left(\dfrac{2}{4}+\dfrac{3}{4}\right)^2\)
\(=-\dfrac{2}{3}-4\cdot\dfrac{25}{16}=-\dfrac{2}{3}-\dfrac{25}{4}\)
\(=-\dfrac{8}{12}-\dfrac{75}{12}=-\dfrac{83}{12}\)
e: \(2\cdot\left(-1\right)^6+\left(\dfrac{3}{4}\right)^2-\dfrac{3}{8}\)
\(=2\cdot1+\dfrac{9}{16}-\dfrac{3}{8}\)
\(=2+\dfrac{9}{16}-\dfrac{6}{16}=2+\dfrac{3}{16}=\dfrac{35}{16}\)
f: \(\left[\left(\dfrac{3}{5}-\dfrac{1}{3}\right)\cdot6+\dfrac{-1}{3}\right]\cdot5\)
\(=\left[\dfrac{9-5}{15}\cdot6+\dfrac{-1}{3}\right]\cdot5\)
\(=\left(\dfrac{4}{15}\cdot6-\dfrac{1}{3}\right)\cdot5=\dfrac{19}{15}\cdot5=\dfrac{19}{3}\)
g: \(\dfrac{3}{4}:\left(\dfrac{2}{3}-\dfrac{5}{9}\right)+\dfrac{9}{4}=\dfrac{3}{4}:\dfrac{6-5}{9}+\dfrac{9}{4}\)
\(=\dfrac{3}{4}\cdot9+\dfrac{9}{4}=\dfrac{27}{4}+\dfrac{9}{4}=\dfrac{36}{4}=9\)
h: \(0,8:\left\{0,2-8\cdot\left[\dfrac{7}{48}+\left(\dfrac{5}{24}-\dfrac{5}{16}\right)\right]\right\}\)
\(=0,8:\left\{0.2-8\cdot\left[\dfrac{7}{48}+\dfrac{10}{48}-\dfrac{15}{48}\right]\right\}\)
\(=0,8:\left\{0.2-8\cdot\dfrac{2}{48}\right\}\)
\(=0,8:\left\{0.2-\dfrac{1}{3}\right\}=0,8:\left\{\dfrac{1}{5}-\dfrac{1}{3}\right\}=0,8:\dfrac{-2}{15}=0,8\cdot\dfrac{15}{-2}=\dfrac{12}{-2}=-6\)
Bài 1:
a: \(x+\dfrac{-2}{5}=-\dfrac{1}{3}\)
=>\(x=-\dfrac{1}{3}+\dfrac{2}{5}=-\dfrac{5}{15}+\dfrac{6}{15}=\dfrac{1}{15}\)
b: \(0,5-x=-\dfrac{5}{14}\)
=>\(\dfrac{1}{2}-x=-\dfrac{5}{14}\)
=>\(x=\dfrac{1}{2}-\left(-\dfrac{5}{14}\right)=\dfrac{1}{2}+\dfrac{5}{14}=\dfrac{7}{14}+\dfrac{5}{14}=\dfrac{12}{14}=\dfrac{6}{7}\)
c: \(3\dfrac{1}{5}-x=1,6+\dfrac{7}{10}\)
=>\(3,2-x=1,6+0,7=2,3\)
=>x=3,2-2,3=0,9
d: \(\dfrac{11}{12}-\left(x+\dfrac{2}{5}\right)=\dfrac{2}{3}\)
=>\(x+\dfrac{2}{5}=\dfrac{11}{12}-\dfrac{2}{3}=\dfrac{11}{12}-\dfrac{8}{12}=\dfrac{3}{12}=\dfrac{1}{4}\)
=>\(x=\dfrac{1}{4}-\dfrac{2}{5}=\dfrac{5}{20}-\dfrac{8}{20}=-\dfrac{3}{20}\)
e: \(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
=>\(\dfrac{1}{4}:x=\dfrac{2}{5}-\dfrac{3}{4}=\dfrac{8}{20}-\dfrac{15}{20}=-\dfrac{7}{20}\)
=>\(x=-\dfrac{1}{4}:\dfrac{7}{20}=-\dfrac{1}{4}\cdot\dfrac{20}{7}=\dfrac{-5}{7}\)
f: \(\dfrac{3}{4}x-\dfrac{1}{2}=\dfrac{3}{7}\)
=>\(\dfrac{3}{4}x=\dfrac{1}{2}+\dfrac{3}{7}=\dfrac{7}{14}+\dfrac{6}{14}=\dfrac{13}{14}\)
=>\(x=\dfrac{13}{14}:\dfrac{3}{4}=\dfrac{13}{14}\cdot\dfrac{4}{3}=\dfrac{52}{42}=\dfrac{26}{21}\)

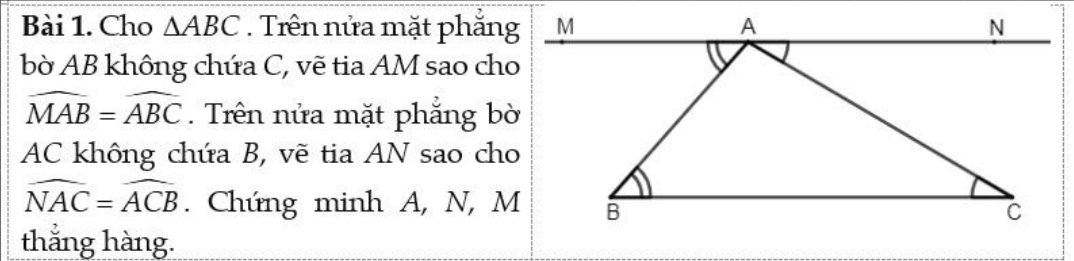
Ta có: \(\widehat{MAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên MA//BC
Ta có: \(\widehat{NAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NA//BC
Ta có: MA//BC
NA//BC
MA,NA có điểm chung là A
Do đó: M,A,N thẳng hàng

Bài 5:
Gọi giá tiền mỗi chiếc áo bạn Hoa đã mua là x(nghìn đồng)
(Điều kiện: x>0)
Giá tiền ban đầu của mỗi chiếc áo là x+30(nghìn đồng)
Số lượng áo dự định là \(\dfrac{600}{x+30}\)(cái)
Số lượng áo thực tế là \(\dfrac{600}{x}\)(cái)
Vì số lượng áo thực tế mua được bằng 1,25 lần số lượng áo ban đầu định mua thì \(\dfrac{600}{x}=1,25\cdot\dfrac{600}{x+30}\)
=>\(\dfrac{600}{x}=\dfrac{750}{x+30}\)
=>\(\dfrac{4}{x}=\dfrac{5}{x+30}\)
=>5x=4x+120
=>x=120(nhận)
Vậy: Giá tiền của mỗi chiếc áo thực tế là 120 nghìn đồng


a: \(\left(-\dfrac{2}{5}-\dfrac{4}{3}+\dfrac{1}{4}\right)-\left(\dfrac{3}{5}-\dfrac{1}{3}-\dfrac{3}{4}\right)\)
\(=-\dfrac{2}{5}-\dfrac{4}{3}+\dfrac{1}{4}-\dfrac{3}{5}+\dfrac{1}{3}+\dfrac{3}{4}\)
\(=\left(-\dfrac{2}{5}-\dfrac{3}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{3}\right)+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)\)
=-1-1+1=-1
b: \(\dfrac{2}{5}-\left(\dfrac{4}{3}+\dfrac{4}{5}\right)-\left(-\dfrac{1}{9}-0,4\right)+\dfrac{11}{9}\)
\(=\dfrac{2}{5}-\dfrac{4}{3}-\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{2}{5}+\dfrac{11}{9}\)
\(=\left(\dfrac{2}{5}-\dfrac{4}{5}+\dfrac{2}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{9}+\dfrac{11}{9}\right)\)
\(=0+\left(-\dfrac{4}{3}+\dfrac{12}{9}\right)=0\)
c: \(\dfrac{11}{8}\cdot\left[\left(-\dfrac{5}{11}:\dfrac{13}{8}-\dfrac{5}{11}:\dfrac{13}{5}\right)+\dfrac{-6}{33}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\cdot\dfrac{8}{13}-\dfrac{5}{11}\cdot\dfrac{5}{13}-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\left(\dfrac{8}{13}+\dfrac{5}{13}\right)-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left(-\dfrac{5}{11}-\dfrac{2}{11}\right)+\dfrac{3}{4}=\dfrac{-7}{8}+\dfrac{3}{4}=-\dfrac{1}{8}\)
d: \(A=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)+\dfrac{4}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)+\dfrac{4}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\dfrac{-9}{15}+\dfrac{4}{9}:\dfrac{-3}{22}\)
\(=\dfrac{4}{9}\cdot\dfrac{-5}{3}+\dfrac{4}{9}\cdot\dfrac{-22}{3}=\dfrac{4}{9}\cdot\left(-\dfrac{5}{3}-\dfrac{22}{3}\right)=\dfrac{4}{9}\left(-9\right)=-4\)

a: Sửa đề; OA<OB
Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
=>AD=BC
b: Ta có: ΔOAD=ΔOCB
=>\(\widehat{OAD}=\widehat{OCB};\widehat{ODA}=\widehat{OBC}\)
Ta có: OA+AB=OB
OC+CD=OD
mà OA=OC và OB=OD
nên AB=CD
Ta có: \(\widehat{OAD}+\widehat{DAB}=180^0\)(hai góc kề bù)
\(\widehat{OCB}+\widehat{DCB}=180^0\)
mà \(\widehat{OAD}=\widehat{OCB}\)
nên \(\widehat{DAB}=\widehat{DCB}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có:ΔEAB=ΔECD
=>EB=ED; EA=EC
Xét ΔOEB và ΔOED có
OE chung
OB=OD
EB=ED
Do đó: ΔOEB=ΔOED
=>\(\widehat{BOE}=\widehat{DOE}\)
=>OE là phân giác của góc xOy


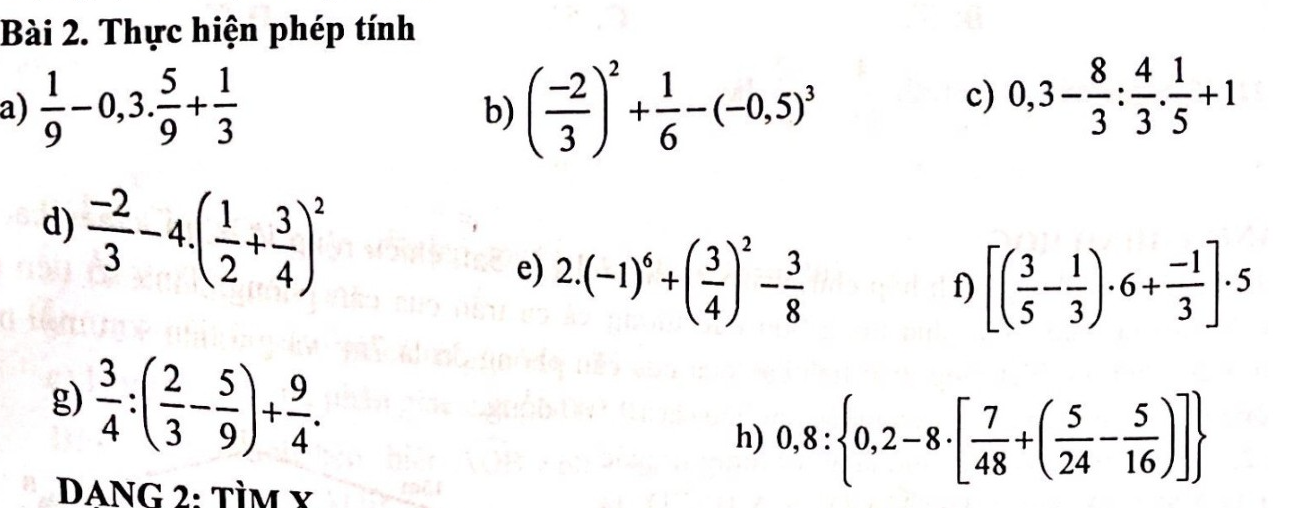
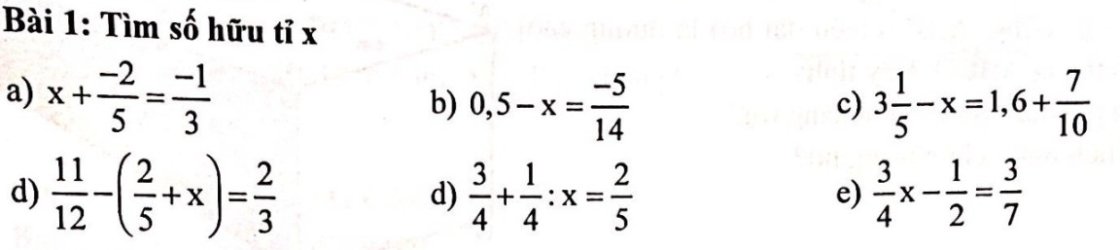

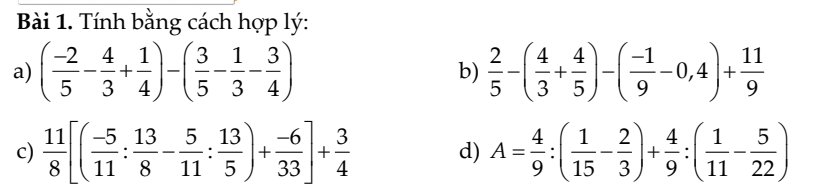
AB//CD
=>\(y=\widehat{BDC}\)(hai góc so le trong)
=>\(y=45^0\)
AB//CD
=>\(x+100^0=180^0\)
=>\(x=80^0\)
\(x-y=80^0-45^0=35^0\)