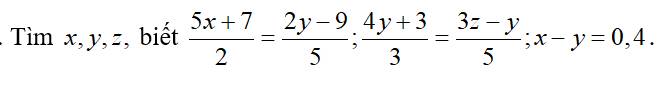Cho a;b;c;d là các số nguyên dương và thỏa mãn: (a/b)<(c/d). tìm một số hữu tỉ x sao cho (a/b)<x<(c/d), từ đó chúng minh rằng ta có thể tìm được các số hữu tỉ khác nhau nằm giữa hai số 1 và 2 (khi biểu diễn trên trục số) mà tổng của chúng lớn hớn 2023 (giải theo trình độ lớp 7)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
3
T
7 tháng 1 2024
Thực hiện phép chia \(a\left(x\right)=x^3+2x^2+3x-1\) cho \(b\left(x\right)=x-2\), ta được:
\(a\left(x\right)=\left(x-2\right)\cdot Q\left(x\right)+r\)
\(\Rightarrow a\left(2\right)=\left(2-2\right)\cdot Q\left(2\right)+r=r\)
\(\Rightarrow r=2^3+2\cdot2^2+3\cdot2-1=21\)
Vậy số dư phép chia \(a\left(x\right)\) cho \(b\left(x\right)\) là \(21\).
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2024
Áp dụng tính chất dãy tỉ số bằng nhau:
\(2x=3y=5z\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y-z}{15+10-6}=\dfrac{95}{19}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5.15=75\\y=5.10=50\\z=5.6=30\end{matrix}\right.\)
H
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 1 2024
A = 1 + 21 + 22 + 23 + ...+ 22005
chứ em nhỉ?
NP
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 1 2024
\(x-y\) = 0,4
\(x\) = 0,4 + y
⇒ \(\dfrac{5.\left(0,4+y\right)+7}{2}\) = \(\dfrac{2y-9}{5}\)
⇒5.[5.(0,4 +y) + 7] = (2y - 9).2
⇒ 10 + 25y + 35 = 4y - 18
25y - 4y = - 10 - 35 - 18
21y = - 63
y = -3
\(x\) = -3 + 0,4 = -2,6
\(\dfrac{4y+3}{3}\) = \(\dfrac{3z-y}{5}\)
\(\dfrac{4.\left(-3\right)+3}{3}\) = \(\dfrac{3z-3}{5}\)
-3 = 3.( \(\dfrac{z-1}{5}\))
z - 1 = 3 : \(\dfrac{3}{5}\)
z - 1 = 5
z = 6
7 tháng 1 2024
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!
7 tháng 1 2024
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!
7 tháng 1 2024
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!
7 tháng 1 2024
B) Làm tương tự câu a ta được:
(a+6b); (2a+5b); (3a+4b); (4a+3b); (5a+2b); (6a+b) đều chia hết cho 7 ⇒(a+6b).(2a+5b).(3a+4b).(4a+3b).(5a+2b).(6a+b) chia hết cho 7.7.7.7.7.7 ⇒(a+6b).(2a+5b).(3a+4b).(4a+3b).(5a+2b).(6a+b) chia hết cho 76 (ĐPCM)
Vậy...
7 tháng 1 2024
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!