doanh thu mỗi ngày của một cửa hàng đồ gốm trong 4 ngày kinh doanh được lập thành một tỉ lệ thức biết doanh thu trong 3 ngày là 8 triệu đồng ,4 triệu ddoongfvaf 16 triệu đồng. tìm doanh thu của ngày còn lại
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3x-y=x+2y\)
\(\Rightarrow3x-x=2y+y\)
\(\Rightarrow2x=3y\)
\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{2023x-2022y}{2023\cdot3-2022\cdot2}=\dfrac{4050}{2025}=2\)
\(\left(+\right)\dfrac{x}{3}=2\Rightarrow x=6\)
\(\left(+\right)\dfrac{y}{2}=2\Rightarrow y=4\)
Vậy \(\left(x;y\right)=\left(6;4\right)\)

Lời giải:
$(0,6-1,125+\frac{15}{11}):(-0,3+\frac{9}{16}-\frac{15}{22})$
$=(\frac{15}{11}-0,525):(\frac{-3}{10}+\frac{9}{16}-\frac{15}{22})$
$=\frac{369}{440}: \frac{-369}{880}=\frac{-880}{440}=-2$

a) xét ΔAMB và ΔEMC, có:
MB = MC (gt) (1)
\(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)
MA = ME (gt) (2)
⇒ ΔAMB = ΔEMC (c-g-c)
b) từ (1) và (2) ⇒ tứ giác ABEC là hình bình hành
⇒ AC // BE
c) vì ΔAMB = ΔEMC (câu a)
⇒ AB = EC (2 cạnh tương ứng)
d) vì AC // BE (câu b)
\(\widehat{CAE}=\widehat{BEA}\) (so le trong)
xét ΔMAN và ΔMEP, có:
AN = EP (GT)
\(\widehat{CAE}=\widehat{BEA}\) (chứng minh trên)
ME = MA (gt)
⇒ ΔMAN = ΔMEP (c-g-c)
⇒ MN = MP (2 cạnh tương ứng) (3)
lại có AN = PE (gt) ⇒ M ∈ NP (4)
từ (3) (4) ⇒ 3điểm MNP thẳng hàng

Lời giải:
Ta thấy $(x+1)^2\geq 0$ với mọi $x$
$\Rightarrow 2(x+1)^2\geq 0$
$\Rightarrow 2(x+1)^2-3\geq 0-3=-3$
Vậy GTNN của biểu thức là $-3$. Giá trị này đạt được tại $x+1=0$
$\Leftrightarrow x=-1$
---------------------------
$(2x-1)^2\geq 0$ với mọi $x$
$\Rightarrow 4-(2x-1)^2\leq 4-0=4$
Vậy GTLN của biểu thức là $4$. Giá trị này đạt được tại $2x-1=0$
$\Leftrightarrow x=\frac{1}{2}$

a) Cho \(A\left(x\right)=0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Vậy nghiệm của đa thức A(x) là \(x=2\)
b) Cho \(B\left(x\right)=0\)
\(\Rightarrow\dfrac{3}{4}=0\) (vô lý)
Vậy đa thức B(x) không có nghiệm
c) Cho \(C\left(x\right)=0\)
\(\Rightarrow x^2-1=0\)
\(\Rightarrow x^2=1\)
\(\Rightarrow x=-1;x=1\)
Vậy đa thức C(x) có nghiệm: \(x=-1;x=1\)
d) Cho \(D\left(x\right)=0\)
\(\Rightarrow x^2+x=0\)
\(\Rightarrow x\left(x+1\right)=0\)
\(\Rightarrow x=0\) hoặc \(x+1=0\)
*) \(x+1=0\)
\(\Rightarrow x=-1\)
Vậy đa thức D(x) có nghiệm: \(x=-1;x=0\)

Tính diện tích hình H,biết hình chữ nhật có chiều dài 8 cm,chiều rộng là 3 cm,hình vuông có cạnh là 3 cm.

Do \(x,y,z\) là số chính phương nên chỉ có thể chia 3 và 4 dư 0 hoặc dư 1.
Theo nguyên lí Dirichlet, tồn tại 2 số có cùng số dư khi chia cho 3 và 4. Không mất tính tổng quát, giả sử là \(x,y\)
\(\Rightarrow\left\{{}\begin{matrix}x-y⋮3\\x-y⋮4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}B⋮3\\B⋮4\end{matrix}\right.\) \(\Rightarrow B⋮12\), đpcm

Lời giải:
a.
$Q(x)=(3x^4+x^3+2x^2+x+1)-P(x)=(3x^4+x^3+2x^2+x+1)-(2x^4-x^2+x-2)$
$=3x^4+x^3+2x^2+x+1-2x^4+x^2-x+2$
$=x^4+x^3+3x^2+3$
b.
$H(x)=P(x)-(x^4-x^3+x^2-2)=(2x^4-x^2+x-2)-(x^4-x^3+x^2-2)$
$=2x^4-x^2+x-2-x^4+x^3-x^2+2$
$=x^4+x^3-2x^2+x$
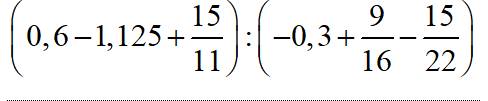
Vì doanh thu 4 ngày lập thành tỉ lệ thức lần lượt là:
Ngày \(1,2,3\) tương ứng với \(8\) triệu đồng, \(4\) triệu đồng và \(16\) triệu đồng.
\(\Rightarrow\) Ta có:
Gọi doanh thu của ngày còn lại là \(d\).
\(\dfrac{8}{4}=\dfrac{16}{d}\) \(\Rightarrow d=8\) triệu đồng.
Vậy doanh thu của ngày còn lại là \(8\) triệu đồng.