Danh sách các thí sinh nhận thưởng cuộc thi Học cùng Olm mỗi ngày học giỏi, học hay toàn quốc 2024. Sự kiện hóa học vì sao Z là số hiệu nguyên tử và Danh sách thí sinh đạt giải cuộc thi thông điệp người phụ nữ em yêu thương.
Cô Thương Hoài thân ái chào toàn thể các học viên của Olm. Hôm nay là ngày đặc biệt, hết sức đặc biệt chỉ duy nhất có tại diễn đàn Olm đó là hàng loạt các học viên của Olm sẽ được nhận thưởng vào ngày vô cùng ý nghĩa này. Đây sẽ là món quà tinh thần quý giá mà các thí sinh tặng cho mẹ của mình.
Để nhận thưởng các em làm các yêu cầu sau:
Bình luận thứ nhất: Em đăng ký nhận thưởng: ...... (chọn tên sự kiện mình được thưởng điền vào chỗ trống ví dụ: Em đăng ký nhận quà nhà tài trợ cuộc thi học cùng Olm mỗi ngày học giỏi học hay)
Bình luận thứ hai: Em đăng kí nhận:.... (chọn hình thức mà mình được thưởng điền vào chỗ ...)
Thời hạn nhận thưởng từ khi có thông báo đến 24 giờ ngày 21 tháng 10 năm 2024. Sau thời hạn này giải thưởng sẽ được thu hồi theo quy định
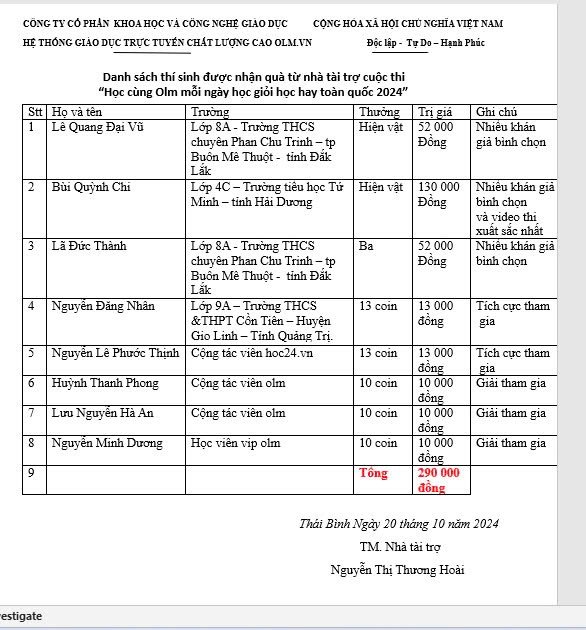
1; Danh sách các thí sinh được nhận quà từ nhà tài trợ cuộc thi Học cùng Olm mỗi ngày học giỏi học hay.
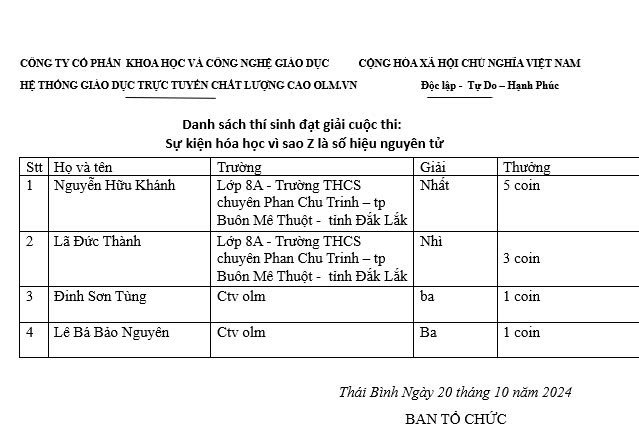
2; Danh sách thí sinh đạt giải sự kiện hóa học:
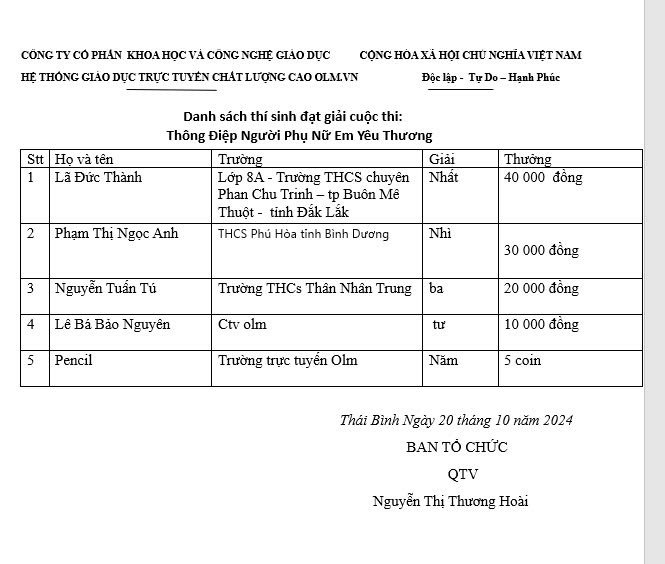
Danh sách thí sinh đạt giải cuộc thi thông điệp người phụ nữ em yêu thương:
Cuối cùng chúc toàn thể các em có một ngày nghỉ lễ vui vẻ, an nhiên bên gia đình!

Em đăng ký nhận quà nhà tài trợ cuộc thi học cùng Olm mỗi ngày học giỏi học hay
Em đăng ký nhận coin từ nhà tài trợ cuộc thi học cùng Olm mỗi ngày học giỏi học hay.